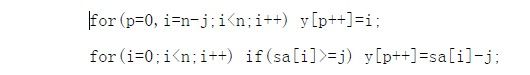首先吐槽一句：大神就是大神，写的东西我理解了三个月终于沾到边了！
进入正题：http://wenku.baidu.com/view/ed1be61e10a6f524ccbf85fd.html
建议跟pdf一起看
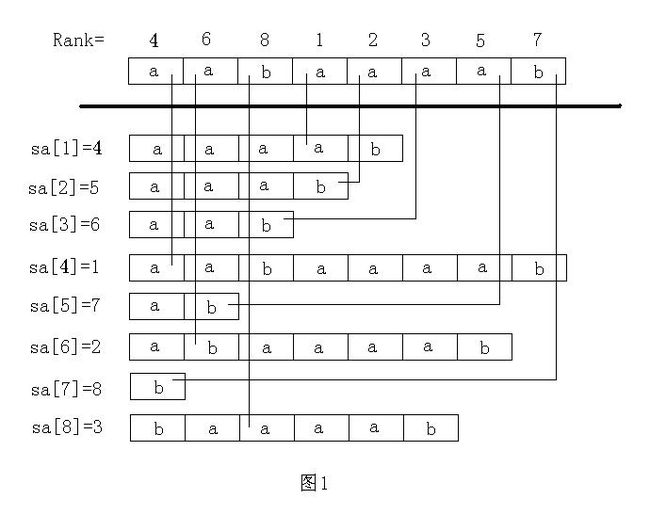
上图是后缀数组具体怎么存储的
（主要笔记就是关于倍增算法的）
先看一看程序：
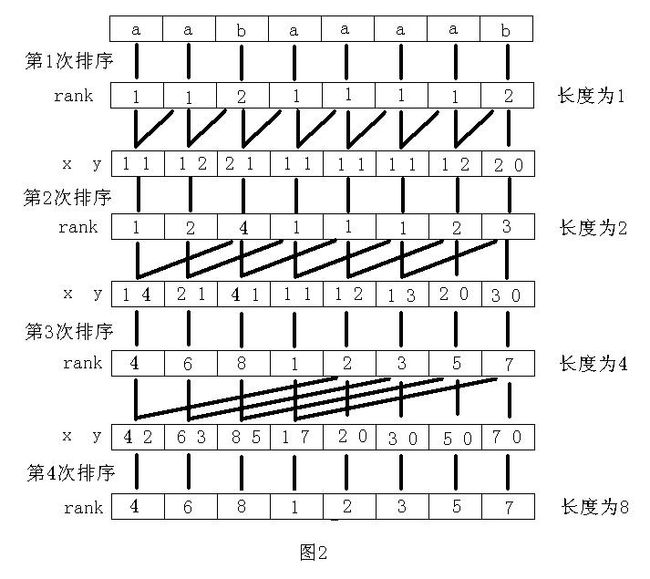
这一段是对长度为1的字符串进行排序，论文上写的很清楚，自己划划就知道了
接下来：
第一句话： y[p++]=i; 想一想，此时我们考虑这个字符串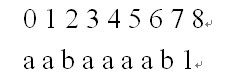
i的值为8，那么也就是说i+j的r值（r[i+j]）永远小于0-8中的任何数！那么毫无疑问这个y值是最小的，所以可以直接排在前面
对于y数组的理解，我是这么想的：y[i]表示排名为i的标号为y[i](第二关键字排序)
然后利用y数组将x数组排好序
下面的一行很重要：
注意：必须倒着来！！！！！ ws[wv[i]]理解：wv[i]表示：y值排名为i的对应编号为y[i]，的x值
y数组第一次的值是：8 7 0 2 3 4 5 1 6（从0开始）
ws[wv[i]]表示这个x值所有多少个（计数排序），那么这个x值实际上是不知道谁排前面谁排后面的，只有通过y值确定
但由于--ws[wv[i]]，所以这个是递减的！那么y[i]的值也就应该是最差的!所以应该倒着！
接下来的我就没看了。
二：对于height数组的理解
核心是这个：
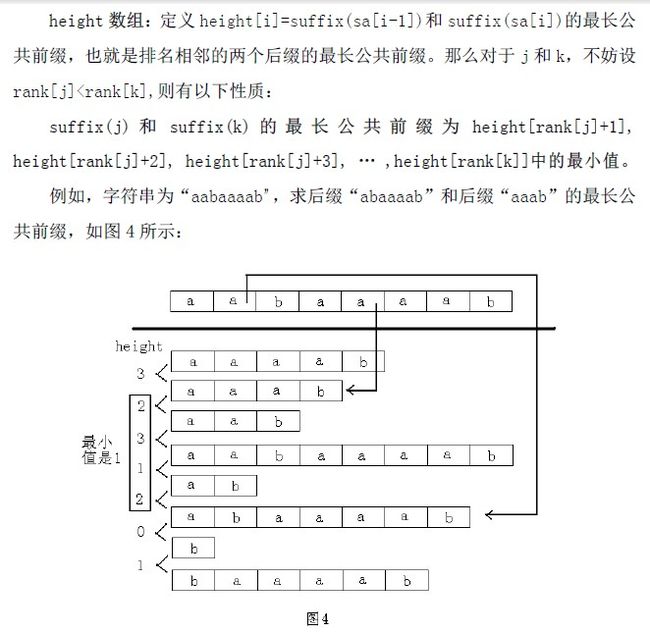
为什么h[i]>=h[i-1]-1
h[i]表示：在排好序的字符串中第i名与第i-1名的公共前缀！
举个例子：当i=4时,排名第4的字符串是aabaaaab，排名第4-1的字符串是aab，所以h[i]=3;
开始证明：
当i=0时，字符串为aabaaaab(此时是按照原字符串的顺序)，它的排名为4(rank值已求出)，它的前面一项为3:aab
很明显，h[i]为3
当i=1时，字符串为abaaaab，我们同样也把aab的第一个首字母去掉变成ab,那么很显然，ab与abaaaab的最长前缀为h[i]-1
注意：我们已经知道aab排在aabaaaab前面，那么ab就一定排在abaaaab的前面，所以，不管abaaaab的前一项是多少，它的h值必定大于h[i]-1!!。
上述是当两个首字母相等的时候，那么如果首字母都不相等，那么显然h[i-1]=0,h[i]>=h[i-1]-1必定成立，证毕。
P.S.：还有不对不完善的地方请指正~