图的遍历分为深度优先遍历(Depth_First_Search)和广度优先遍历(Breadth_First_Search),
分别简称为DFS和BFS。
图的遍历是从某一个顶点出发,访问其他顶点,但是不能重复访问(每个顶点只能访问一次)。
深度优先遍历(DFS):
深度优先,就是沿着某一个方向不重复的一直便利下去,若走到尽头,退到上一个顶点,寻找附近有没有顶点,有且不重复的话,接着便利,否则退到上一个顶点。
下面我来讲解下DFS到底是怎么样实现的……
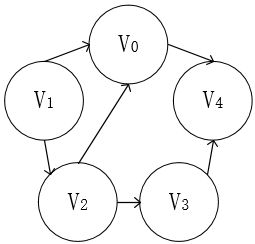
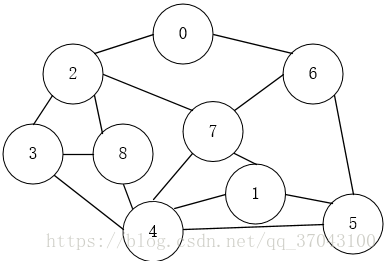
以下面的图为例吧,,
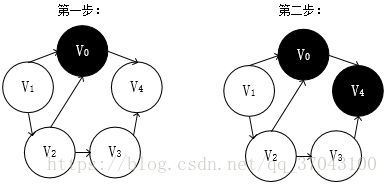
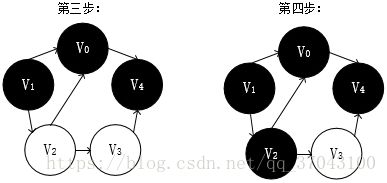
下面是这个图的DFS遍历过程(黑色背景表示已访问过):
上面的遍历过程我来解释下:
我们起始位置时V0,根据箭头的指向,V0->V4,
然后V4周围没有邻接点了,退到V0,V0周围除了V4也没有邻接点(不能重复访问顶点),
接着我们新找一个顶点V1,V1周围有V0和V2,V0已访问过,遍历V2,V1->V2,
V2周围有V0和V3,遍历V3,V1->V2->V3,
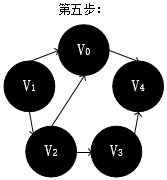
V3周围有V2和V4,遍历V4,V1->V2->V3->V4,
V4周围有V0和V3,返回上一个顶点,指到结束。
emmm,下面我用了邻接矩阵的方式,
对了,邻接矩阵其实也可以自己构建,只要把每个顶点与另一个顶点之间的关系写对,就行了
代码如下:
#include
using namespace std;
bool visited[5]; //标记顶点是否访问过
//邻接矩阵
int MGraph[5][5] = {
{0, 0, 0, 0, 1},
{1, 0, 1, 0, 0},
{1, 0, 0, 1, 0},
{0, 1, 0, 0, 1},
{0, 0, 0, 0, 0}
};
//DFS
void DFS(int MGraph[][5], int i)
{
visited[i] = true;
cout << i;
for(int j = 0; j < 5; j++)
{
if(MGraph[i][j] && !visited[j])
DFS(MGraph, j);
}
}
void DFSTraverse(int MGraph[][5])
{
for(int i = 0; i < 5; i++)
visited[i] = false; //将顶点初始化为未访问
for(int i = 0; i < 5; i++)
{
if(!visited[i]) //对未访问过的顶点调用DFS,如是连通图,只执行一次(我这个不是连通图)
DFS(MGraph, i);
}
}
int main()
{
DFSTraverse(MGraph);
return 0;
}
时间复杂度:若顶点数是n,因为是邻接矩阵,它是个二维数组遍历完成则需要O(n^2)。
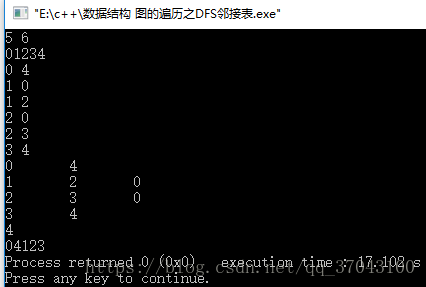
运行结果:
遍历的结果是:04123,与上图对应。
下面是邻接表的代码(DFS是主体,邻接表的代码就不需要看了):
#include
using namespace std;
//开始 邻接表请看上一节
#define MAXVERTEX 100
typedef char vertextype;
typedef struct ArcNode
{
int adjvex;
struct ArcNode *next;
}ArcNode;
typedef struct VertexNode
{
vertextype data;
ArcNode *firstarc;
}VertexNode, AdjList[MAXVERTEX];
typedef struct
{
AdjList adjlist;
int numvertex;
int numarc;
}GraphAdjList;
void CreateAdjListGraph(GraphAdjList &G)
{
ArcNode *e;
cin >> G.numvertex;
cin >> G.numarc;
for(int i = 0; i < G.numvertex; i++)
{
cin >> G.adjlist[i].data;
G.adjlist[i].firstarc = NULL;
}
for(int k = 0; k < G.numarc; k++)
{
int i, j;
cin >> i >> j;
e = new ArcNode;
e->adjvex = j;
e->next = G.adjlist[i].firstarc;
G.adjlist[i].firstarc = e;
}
}
//打印邻接表
void PrintfGraphAdjList(GraphAdjList G)
{
for(int i = 0; i < G.numvertex; i++)
{
ArcNode *p = G.adjlist[i].firstarc;
cout << G.adjlist[i].data << '\t';
while(p)
{
cout << p->adjvex << '\t';
p = p->next;
}
cout << endl;
}
}
//邻接表 结束
bool visited[5]; //用于判断顶点是否被访问过
//DFS
void DFS(GraphAdjList G, int i)
{
ArcNode *p;
p = G.adjlist[i].firstarc;
visited[i] = true; //将访问过的顶点置位true
cout << G.adjlist[i].data;
while(p)
{
if(!visited[p->adjvex])
DFS(G, p->adjvex);
p = p->next;
}
}
void DFSTraverse(GraphAdjList G)
{
for(int i = 0; i < G.numvertex; i++)
visited[i] = false; //将顶点初始化为未访问状态
for(int i = 0; i < G.numvertex; i++)
{
if(!visited[i]) //若顶点没被访问过
DFS(G, i);
}
}
int main()
{
GraphAdjList G;
CreateAdjListGraph(G);
PrintfGraphAdjList(G);
DFSTraverse(G);
return 0;
}
时间复杂度:顶点数是n,边数是e,顶点循环是n,加上DFS里面while(p),边循环了e次,所以是O(n + e)。
运行结果:
两个运行结果都是04123,,,
广度优先遍历(BFS):
从一点出发,先寻找离它最近的几个顶点,然后继这几个顶点再次深入,但是每次搜寻的都是同一级别的(根据离顶点的距离)。
下面我画一个图:
深度优先遍历(DFS):
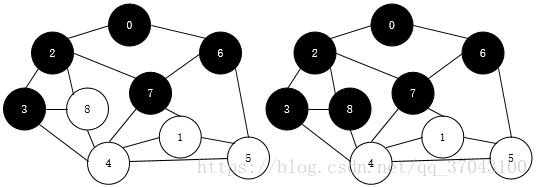
下面是遍历过程(左右上下的顺序):
emmm,解释下这个遍历过程,不过相信大家也能看懂吧(按照离起始点的远近依次访问)
广度搜索,也就是优先广范围搜索,我们从顶点0开始访问,先访问离它最近的顶点,2和6
这样0->2->6
然后再从2开始访问离它最近的顶点3,7和8
这样0->2->6->3->7->8
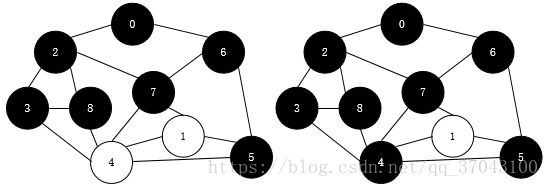
然后退回去再从离6最近的5和7访问,7访问过
这样0->2->6->3->7->8->5
然后是3周围的4,接着是7周围的1,这样我们就全部遍历了
最后的流程是0->2->6->3->7->8->5->4->1
然后理解了它的思想后就是代码了,下面是邻接矩阵的BFS:
#include
#include
using namespace std;
//邻接矩阵
int mgraph[9][9] = {
{0, 0, 1, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 1, 1, 0, 1, 0},
{1, 0, 0, 1, 0, 0, 0, 1, 1},
{0, 0, 1, 0, 1, 0, 0, 0, 1},
{0, 1, 0, 1, 0, 1, 0, 0, 1},
{0, 1, 0, 0, 1, 0, 1, 0, 0},
{1, 0, 0, 0, 0, 1, 0, 1, 0},
{0, 1, 1, 0, 1, 0, 1, 0, 0},
{0, 0, 1, 1, 1, 0, 0, 0, 0}
};
//定义一个队列
queue q;
// 定义判断顶点是否被访问过的数组
bool visited[9];
//BFS
void BFSTraverse(int mgraph[][9])
{
for(int i = 0; i < 9; i++)
visited[i] = false;
for(int i = 0; i < 9; i++)
{
if(!visited[i])
{
cout << i;
visited[i] = true;
q.push(i);
}
while(!q.empty())
{
i = q.front();
q.pop();
for(int j = 0; j < 9; j++)
{
if(mgraph[i][j] == 1 && !visited[j])
{
visited[j] = true;
cout << j;
q.push(j);
}
}
}
}
}
int main()
{
BFSTraverse(mgraph);
return 0;
} 时间复杂度:与DFS一样还是O(n^2),
运行结果:
对吧,只要邻接矩阵构建的没有问题,运行结构就跟上面所构造的图一样。
接着是邻接表的BFS代码:
#include
#include
using namespace std;
//开始 邻接表请看上一节
#define MAXVERTEX 100
typedef char vertextype;
typedef struct ArcNode
{
int adjvex;
struct ArcNode *next;
}ArcNode;
typedef struct VertexNode
{
vertextype data;
ArcNode *firstarc;
}VertexNode, AdjList[MAXVERTEX];
typedef struct
{
AdjList adjlist;
int numvertex;
int numarc;
}GraphAdjList;
void CreateAdjListGraph(GraphAdjList &G)
{
ArcNode *e;
cin >> G.numvertex;
cin >> G.numarc;
for(int i = 0; i < G.numvertex; i++)
{
cin >> G.adjlist[i].data;
G.adjlist[i].firstarc = NULL;
}
for(int k = 0; k < G.numarc; k++)
{
int i, j;
cin >> i >> j;
e = new ArcNode;
e->adjvex = j;
e->next = G.adjlist[i].firstarc;
G.adjlist[i].firstarc = e;
e = new ArcNode;
e->adjvex = i;
e->next = G.adjlist[j].firstarc;
G.adjlist[j].firstarc = e;
}
}
//打印邻接表
void PrintfGraphAdjList(GraphAdjList G)
{
for(int i = 0; i < G.numvertex; i++)
{
ArcNode *p = G.adjlist[i].firstarc;
cout << G.adjlist[i].data << '\t';
while(p)
{
cout << p->adjvex << '\t';
p = p->next;
}
cout << endl;
}
}
//邻接表 结束
//定义一个队列
queue q;
// 定义判断顶点是否被访问过的数组
bool visited[9];
//BFS
void BFSTraverse(GraphAdjList G)
{
ArcNode *p;
for(int i = 0; i < 9; i++)
visited[i] = false;
for(int i = 0; i < 9; i++)
{
if(!visited[i])
{
cout << i;
visited[i] = true;
q.push(i);
}
while(!q.empty())
{
i = q.front();
q.pop();
p = G.adjlist[i].firstarc;
while(p)
{
if(!visited[p->adjvex])
{
visited[p->adjvex] = true;
cout << p->adjvex;
q.push(p->adjvex);
}
p = p->next;
}
}
}
}
int main()
{
GraphAdjList G;
CreateAdjListGraph(G);
PrintfGraphAdjList(G);
BFSTraverse(G);
return 0;
} 时间复杂度:O(n + e)。
运行结果:
emmm,虽然结果和上面不一样,但是层次都是一样的,按照离起始点的距离
分为4层,第一层是0,第二层是26,第三层是3578,第四层是14,输入的顺序不对,然后排出来的就不对,然是层次肯定是对的。
emmm,就这样吧!