《大数据算法》一3.5 寻找频繁元素的随机算法

本节书摘来华章计算机《大数据算法》一书中的第3章 ，第3.5节，王宏志　编著, 更多章节内容可以访问云栖社区“华章计算机”公众号查看。

3.5　寻找频繁元素的随机算法

本节重新研究3.3节中讨论的问题，提出寻找频繁元素的随机算法。Misra-Gries算法通过扫描数据一次提供足够的信息，然后通过第二次扫描数据解决频繁元素发现问题，即扫描数据第一次过程中Misra-Gries算法计算一个数据结构，对于j∈［n］该数据结构可以获得其频率fj的足够准确估计fj。本小节提出另外两个频率估计的随机算法。

3.5.1　略图法

1.略图和线性略图
在处理数据流σ的过程中，令表示Misra-Gries算法中所需的数据结构。这种数据结构的一个缺点是缺少一种通用的方法从和中计算其中“”代表数据流的连接。很明显，需要这种数据结构上的连接操作，如果一个数据结构支持这种连接操作，则该数据结构称为略图，具体定义如下。
　　定义3-3　D(σ)是一种以流的方式处理流σ的数据结构，这种数据结构称为略图，如果有一个空间有效组合算法COMB，对于任意两个数据流σ1和σ2，计算

本节的每个算法都有很好的性质，就定义3-3的意义而言，这些算法能计算输入流的略图。因为这些算法要计算由σ决定的频率向量f(σ)，它们的略图会自然成为f(σ)的函数。事实上，它们应当是线性函数，这涉及另外一个定义。
　　定义3-4　略图算法“sk”称为线性略图，如果对于每个域［n］上的数据流σ，sk(σ)的取值范围在l=l(n)维的向量空间上，并且sk(σ)是f(σ)的线性函数。在这种情况下，l称为线性略图的纬度。
注意，对于线性略图的结合算法只是仅仅在相应向量空间上增加略图。
除了不能产生略图，Misra-Gries算法还有其他缺点，就是不能延伸到十字转门（甚至严格的十字转门）模型。但是本节的算法能够实现，因为基于线性略图的数据流算法从一般模型到十字转门模型都是通用的。如果在一般模型中的j使我们向略图增加一个向量vj，然后十字转门模型中修正的（j,c）在略图中增加cvj，这样可以处理c≥0和c<0的不同情况。
2.计数略图
现在我们描述第一个略图算法，称为“计数略图”。我们从基本略图开始讨论，这个略图已经包含了大部分所需思想。这个略图有一个极小并且是正数的精度参数ε。算法3-5　元素频率计数略图算法

初始化:
1　C［1,…,k］←0，其中k=3/ε2;
2　从2通用函数族中随机选择哈希函数h:［n］→［k］;
3　从2通用函数族中随机选择哈希函数g:［n］→{-1,1};
处理(j,c):
4　C［h(j)］←C［h(j)］+cg(j);
输出:
5　对于查询a,输出f→a=g(a)C［h(a)］。

通过这个算法计算的略图是一个计数器数组C，这个数组可以看作zk上的一个向量。若要使两个略图是可结合的，则它们必须基于同样的哈希函数h和g。
使用该算法，对数据流片段给出的示例如图3-3所示。依据(j,c)值不断计算h(j)、g(j)使用更新C［h(j)］的值。计算过程如下：

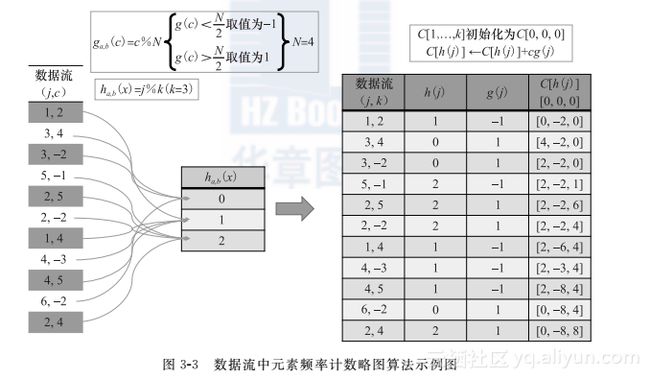
针对每个数据流计算其h(j)、g(j),更新C［h［j］］的值。对于查询a使用最后更新数组C进行计算，输出估计值。
3.计数略图质量分析
定理3-6　对于任意查询a，算法3-5生成的估计满足
证明　固定查询a，考虑基于查询a的输出X=fa。对于每个j∈［n］，当h(j)=h(a)时，让Yj作为指示器，有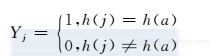
0，h(j)≠h(a)　　检查算法的工作原理，我们发现当且仅当h(j)=h(a)时，j对计数器C［h(a)］有贡献，并且贡献的总和是随机符号g(j)的fj倍。因此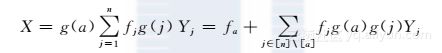，因为g和h是独立的，所以有因此，通过期望的线性度，有因此，输出X=fa是一个对于所需频率fa的无偏估计量。
我们仍然需要证明X不可能偏离其平均值太多。为此，我们分析其差异。根据2-通用哈希函数族的性质，对于每个
有　下一步，我们利用g所对应2-通用函数族的性质，以及g和h的独立性，可总结出对于所有有　因此可计算得到(根据式（3-9）、式(3-11)和式(3-12))
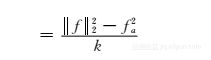(3-13)其中f=f(σ)是由σ决定的频率分布。从式（3-10）到式（3-13），用切比雪夫不等式得到　　对于
，我们定义f-j为（n-1）维的向量，这个向量通过去掉输入f的第j维元素得到，有因此，我们可以用下面这个更加深刻的形式重写上面的公式。.改进略图
略图即通常所说的“计数略图”，这实际上是通过对上述基本略图应用中位数技巧（参见3.4节）获得的略图，对于给定的足够小的δ>0，使其错误的概率降到δ。因此，计数略图可看作二维计数器数组，其中每一个数据流中的元素导致流中若干计数器的更新。为了完整起见，我们用下述算法讨论之。

初始化:
1　C［1,…,t］［1,…,k］←0,其中k=3/ε2且t=O(log(1/δ));
2　从2通用哈希函数族中随机选择哈希函数h1，…，ht:［n］→［k］,
3　从2通用哈希函数族中随机选择哈希函数g1，…，gt:［n］→［lk］;
处理(j,c):
4　for i=1 to t do C［i］［hi(j)］←C［i］［hi(j)］+cgi(j);
输出:
5　对于查询a,输出fa=median1≤i≤tgi(a)C［i］［hi(a)］。

像3.4节一样，可以使用一个标准的切尔诺夫界参数证明估计量fa满足Pr［fa-fa≥εf-a2］≤δ通过适当选择哈希函数族，我们能将哈希方程存储在O(tlog n)的空间。在略图中的每个tk计数器占据O(log m)的空间。这就给我们一个整体的限制空间，即　计数最小略图
另一种频率评估的解决方案就是所谓的“计数最小略图”。与计数略图相同，这个略图也采用一个精度参数ε和一个误差概率参数δ，并包含一个t×k的二维计数数组，用基于哈希函数的方法来更新。t和k的值基于ε和δ来设置，伪代码如下所示。算法3-6　计数最小略图算法

初始化:
1　C［1，…，t］［1，…，k］←0→,其中k=2/ε,t=log(1/δ);
2　从2通用哈希函数族中选取t个哈希函数h1，…，ht:［n］→［k］；
处理(j,c)：
3　for i=1 to t do C［i］［hi(j)］←C［i］［hi(j)］+c;
输出：
4　在查询a中，令fa=min1≤i≤tC［i］［hi(a)］。

注意这个算法相比计数略图简单了很多，另外，还要注意其占用空间为这要比计数略图好1/ε倍。计数最小略图的缺点在于它的近似比保证，这也是我们接下来将要分析的。
计数最小略图质量分析
我们关注当每个流中的元素（j,c）满足c>0的情况,也就是现金注册模型，显然，在这种情况下，每个对应元素a的计数器是对fa的过高估计,这样总有其中fa是算法输出的fa的评估。
定理3-7　
证明　对于固定的a，现在我们分析在计数器中超出真实值的部分。令随机变量Xi表示超出真实值的部分。对于,令Yi,j作为事件hi(j)=hi(a)的指示。注意当且仅当Yi,j=1且被触发时，j作用于计数器C［i］［hi(a)］，它使得fj被加入这个计数器。这样有由于hi是2通用哈希函数族，因此得到这样，通过数学期望的线性可加性可得对于每个fj≥0,有Xi≥0，我们可以通过选择的k值应用马尔可夫不等式得到　上述概率是对于一个计数器进行分析的结果。我们有t个这样的计数器，且它们相互独立。输出中的fa-fa是Xi中的最小值，其中i∈［t］。这样有
≤12t通过对t的选择，可以让这个概率最大为δ。■
至此，我们证明了，最高概率时，有其中左不等式总是成立，右不等式在概率为最大δ时失效。
这个评估弱于计数略图,其原因是它的偏差以εf-a1为界，而不是εf-a2。对于所有矢量z∈Rn，有这个不等式在z有一个非零项时是紧的。且当z中所有值的绝对值都相等时最弱，此时两个范数相差因子n。这样，当流的频率向量更加分散时，与计数最小略图相比,计数略图的评估质量将会提升。