浅谈SMOTE之类不平衡过采样方法
本文是接着上篇MAHAKIL过采样方法写得。SMOTE方法算是现在比较流行的过采样方法了,其分为SMOTE-Regular, SMOTE-Borderline1, SMOTE-Borderline2, SMOTE-SVM这四种方法,应用非常广,而且效果也很好。本篇文章我将主要讲解SMOTE-Regular, SMOTE-Borderline1这两种方法(由于篇幅的原因)并给出相应源码,好了,废话不说直接进正文。
1 SMOTE-Regular算法详解
在实际应用中,读者可能会碰到一种比较头疼的问题,那就是分类问题中类别型的因变量可能存在严重的偏倚,即类别之间的比例严重失调。如欺诈问题中,欺诈类观测在样本集中毕竟占少数;客户流失问题中,非忠实的客户往往也是占很少一部分;在某营销活动的响应问题中,真正参与活动的客户也同样只是少部分。
如果数据存在严重的不平衡,预测得出的结论往往也是有偏的,即分类结果会偏向于较多观测的类。对于这种问题该如何处理呢?最简单粗暴的办法就是构造1:1的数据,要么将多的那一类砍掉一部分(即欠采样),要么将少的那一类进行Bootstrap抽样(即过采样)。但这样做会存在问题,对于第一种方法,砍掉的数据会导致某些隐含信息的丢失;而第二种方法中,有放回的抽样形成的简单复制,又会使模型产生过拟合。
为了解决数据的非平衡问题,2002年Chawla提出了SMOTE算法,即合成少数过采样技术,它是基于随机过采样算法的一种改进方案。该技术是目前处理非平衡数据的常用手段,并受到学术界和工业界的一致认同,接下来简单描述一下该算法的理论思想。
SMOTE算法的基本思想就是对少数类别样本进行分析和模拟,并将人工模拟的新样本添加到数据集中,进而使原始数据中的类别不再严重失衡。该算法的模拟过程采用了KNN技术,模拟生成新样本的步骤如下:
采样最邻近算法,计算出每个少数类样本的K个近邻;
从K个近邻中随机挑选N个样本进行随机线性插值;
构造新的少数类样本;
将新样本与原数据合成,产生新的训练集;
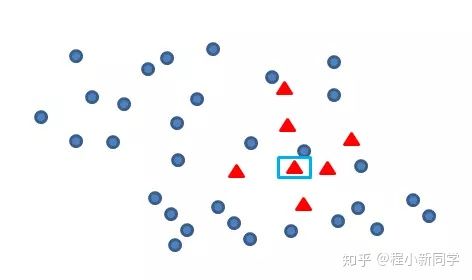
Smote算法的思想其实很简单,先随机选定n个少类的样本,如下图
找出初始扩展的少类样本
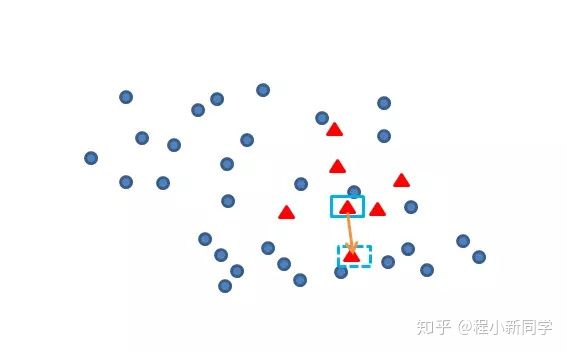
再找出最靠近它的m个少类样本,如下图
再任选最临近的m个少类样本中的任意一点,
在这两点上任选一点,这点就是新增的数据样本
其实原理很简单,这么一说大家一看就知道了。它就是在少数类样本中用KNN方法合成了新样本,而不同于ROS方法随机复制成新样本,所以更具有代表性
以下便是相应源码(SMOTE.py)
from sklearn.neighbors import NearestNeighbors
from base_sampler import *
import numpy as np
# 使用K-近邻方法产生新样本
def make_sample(old_feature_data, diff):
# 获取每一个少数类样本点周围最近的n_neighbors-1个点的位置矩阵
nns = NearestNeighbors(n_neighbors=6).fit(old_feature_data).kneighbors(old_feature_data, return_distance=False)[:,1:]
# 随机产生diff个随机数作为之后产生新样本的选取的样本下标值
samples_indices = np.random.randint(low=0, high=np.shape(old_feature_data)[0], size=diff)
# 随机产生diff个随机数作为之后产生新样本的间距值
steps = np.random.uniform(size=diff)
cols = np.mod(samples_indices, nns.shape[1])
reshaped_feature = np.zeros((diff, old_feature_data.shape[1]))
for i, (col, step) in enumerate(zip(cols, steps)):
row = samples_indices[i]
reshaped_feature[i] = old_feature_data[row] - step * (old_feature_data[row] - old_feature_data[nns[row, col]])
# 将原少数类样本点与新产生的少数类样本点整合
new_min_feature_data = np.vstack((reshaped_feature, old_feature_data))
return new_min_feature_data
# 对不平衡的数据集imbalanced_data_arr2进行SMOTE采样操作,返回平衡数据集
# :param imbalanced_data_arr2: 非平衡数据集
# :return: 平衡后的数据集
def SMOTE(imbalanced_data_arr2):
# 将数据集分开为少数类数据和多数类数据
minor_data_arr2, major_data_arr2 = seperate_minor_and_major_data(imbalanced_data_arr2)
# print(minor_data_arr2.shape)
# 计算多数类数据和少数类数据之间的数量差,也是需要过采样的数量
diff = major_data_arr2.shape[0] - minor_data_arr2.shape[0]
# 原始少数样本的特征集
old_feature_data = minor_data_arr2[:, : -1]
# 原始少数样本的标签值
old_label_data = minor_data_arr2[0][-1]
# 使用K近邻方法产生的新样本特征集
new_feature_data = make_sample(old_feature_data, diff)
# 使用K近邻方法产生的新样本标签数组
new_labels_data = np.array([old_label_data] * np.shape(major_data_arr2)[0])
# 将类别标签数组合并到少数类样本特征集,构建出新的少数类样本数据集
new_minor_data_arr2 = np.column_stack((new_feature_data, new_labels_data))
# print(new_minor_data_arr2[:,-1])
# 将少数类数据集和多数据类数据集合并,并对样本数据进行打乱重排,
balanced_data_arr2 = concat_and_shuffle_data(new_minor_data_arr2, major_data_arr2)
return balanced_data_arr2
# 测试
if __name__ == '__main__':
imbalanced_data = np.load('imbalanced_train_data_arr2.npy')
print(imbalanced_data.shape)
minor_data_arr2, major_data_arr2 = seperate_minor_and_major_data(imbalanced_data)
print(minor_data_arr2.shape)
print(major_data_arr2.shape)
# 测试SMOTE方法
balanced_data_arr2 = SMOTE(imbalanced_data)
print(balanced_data_arr2)
print(balanced_data_arr2.shape)
辅助类依旧是base_sampler.py
""
采样器的基础代码,可用于后面采样器的复用
"""
import numpy as np
import os
def seperate_minor_and_major_data(imbalanced_data_arr2):
"""
将训练数据分开为少数据类数据集和多数类数据集
:param imbalanced_data_arr2: 非平衡数集
:return: 少数据类数据集和多数类数据集
"""
# 提取类别标签一维数组,并提取出两类类别标签标记
labels_arr1 = imbalanced_data_arr2[:, -1]
unique_labels_arr1 = np.unique(labels_arr1)
if len(unique_labels_arr1) != 2:
print('数据类别大于2,错误!')
return
# 找出少数类的类别标签
minor_label = unique_labels_arr1[0] if np.sum(labels_arr1 == unique_labels_arr1[0]) \
< np.sum(labels_arr1 == unique_labels_arr1[1]) else unique_labels_arr1[1]
[rows, cols] = imbalanced_data_arr2.shape # 获取数据二维数组形状
minor_data_arr2 = np.empty((0, cols)) # 建立一个空的少数类数据二维数组
major_data_arr2 = np.empty((0, cols)) # 建立一个空的多数类数据二维数组
# 遍历每个样本数据,分开少数类数据和多数类数据
for row in range(rows):
data_arr1 = imbalanced_data_arr2[row, :]
if data_arr1[-1] == minor_label:
# 如果类别标签为少数类类别标签,则将数据加入少数类二维数组中
minor_data_arr2 = np.row_stack((minor_data_arr2, data_arr1))
else: # 否则,将数据加入多数类二维数组中
major_data_arr2 = np.row_stack((major_data_arr2, data_arr1))
return minor_data_arr2, major_data_arr2
def concat_and_shuffle_data(data1_arr2, data2_arr2):
"""
对两个numpy二维数组进行0轴连接,并对行向量进行打乱重排,
:param data1_arr2: numpy二维数组
:param data2_arr2: numpy二维数组
:return:
"""
data_arr2 = np.concatenate((data1_arr2, data2_arr2), axis=0) # 数组0轴连接
np.random.shuffle(data_arr2) # 行向量shuffle
return data_arr2
if __name__ == '__main__':
imbalanced_train_data_path = '../../data/clean_data/imbalanced_train_data_arr2.npy'
imbalanced_train_data_arr2 = np.load(imbalanced_train_data_path)
minor_data_arr2, major_data_arr2 = seperate_minor_and_major_data(imbalanced_train_data_arr2)
print(minor_data_arr2.shape)
print(major_data_arr2.shape)
以上便将SMOTE-Regular方法介绍完了,大家看完之后是不是觉得还意犹未尽啊,哈哈哈哈哈。别着急下面就给你来介绍SMOTE-Borderline1方法
2 SMOTE-Borderline1算法详解
如果说上面的方法你看懂了之后,那么这个方法你也很容易懂了。其实就是在SMOTE-Regular的基础上改进了一些,即选取的少数样本值集合会更小更具有代表性——在少数类与多数类样本的边缘。确定好之后产生新样本的步骤和SMOTE-Regular没什么区别,都是用选取的少数样本点与其他的距离其最近的少数样本点结合产生新样本(不知道这绕口令大家有没有听懂,哈哈哈哈哈,没听懂的话可以看看下面我贴的论文介绍片段)
SMOTE-Borderline简介
接下来就是贴出该方法的伪代码了,大家看仔细了哈
全英文的伪代码看完了,估计大家现在也晕晕乎乎的。尤其是对于英文不太好的朋友,别急,我这就把源码贴出来,对照源码看事半功倍
from sklearn.neighbors import NearestNeighbors
from sklearn.utils import safe_indexing
from base_sampler import *
import numpy as np
# 处于多数类与少数类边缘的样本
def in_danger(imbalanced_featured_data, old_feature_data, old_label_data, imbalanced_label_data):
nn_m = NearestNeighbors(n_neighbors=11).fit(imbalanced_featured_data)
# 获取每一个少数类样本点周围最近的n_neighbors-1个点的位置矩阵
nnm_x = NearestNeighbors(n_neighbors=11).fit(imbalanced_featured_data).kneighbors(old_feature_data,
return_distance=False)[:,1:]
nn_label = (imbalanced_label_data[nnm_x] != old_label_data).astype(int)
n_maj = np.sum(nn_label, axis=1)
return np.bitwise_and(n_maj >= (nn_m.n_neighbors - 1) / 2, n_maj < nn_m.n_neighbors - 1)
# 产生少数类新样本的方法
def make_sample(imbalanced_data_arr2, diff):
# 将数据集分开为少数类数据和多数类数据
minor_data_arr2, major_data_arr2 = seperate_minor_and_major_data(imbalanced_data_arr2)
imbalanced_featured_data = imbalanced_data_arr2[:, : -1]
imbalanced_label_data = imbalanced_data_arr2[:, -1]
# 原始少数样本的特征集
old_feature_data = minor_data_arr2[:, : -1]
# 原始少数样本的标签值
old_label_data = minor_data_arr2[0][-1]
danger_index = in_danger(imbalanced_featured_data, old_feature_data, old_label_data, imbalanced_label_data)
# 少数样本中噪音集合,也就是最终要产生新样本的集合
danger_index_data = safe_indexing(old_feature_data, danger_index)
# 获取每一个少数类样本点周围最近的n_neighbors-1个点的位置矩阵
nns = NearestNeighbors(n_neighbors=6).fit(old_feature_data).kneighbors(danger_index_data,
return_distance=False)[:, 1:]
# 随机产生diff个随机数作为之后产生新样本的选取的样本下标值
samples_indices = np.random.randint(low=0, high=np.shape(danger_index_data)[0], size=diff)
# 随机产生diff个随机数作为之后产生新样本的间距值
steps = np.random.uniform(size=diff)
cols = np.mod(samples_indices, nns.shape[1])
reshaped_feature = np.zeros((diff, danger_index_data.shape[1]))
for i, (col, step) in enumerate(zip(cols, steps)):
row = samples_indices[i]
reshaped_feature[i] = danger_index_data[row] - step * (danger_index_data[row] - old_feature_data[nns[row, col]])
new_min_feature_data = np.vstack((reshaped_feature, old_feature_data))
return new_min_feature_data
# 对不平衡的数据集imbalanced_data_arr2进行Border-SMOTE采样操作,返回平衡数据集
# :param imbalanced_data_arr2: 非平衡数据集
# :return: 平衡后的数据集
def Border_SMOTE(imbalanced_data_arr2):
# 将数据集分开为少数类数据和多数类数据
minor_data_arr2, major_data_arr2 = seperate_minor_and_major_data(imbalanced_data_arr2)
# print(minor_data_arr2.shape)
# 计算多数类数据和少数类数据之间的数量差,也是需要过采样的数量
diff = major_data_arr2.shape[0] - minor_data_arr2.shape[0]
# 原始少数样本的标签值
old_label_data = minor_data_arr2[0][-1]
# 使用K近邻方法产生的新样本特征集
new_feature_data = make_sample(imbalanced_data_arr2, diff)
# 使用K近邻方法产生的新样本标签数组
new_labels_data = np.array([old_label_data] * np.shape(major_data_arr2)[0])
# 将类别标签数组合并到少数类样本特征集,构建出新的少数类样本数据集
new_minor_data_arr2 = np.column_stack((new_feature_data, new_labels_data))
# print(new_minor_data_arr2[:,-1])
# 将少数类数据集和多数据类数据集合并,并对样本数据进行打乱重排,
balanced_data_arr2 = concat_and_shuffle_data(new_minor_data_arr2, major_data_arr2)
return balanced_data_arr2
# 测试
if __name__ == '__main__':
imbalanced_data = np.load('imbalanced_train_data_arr2.npy')
print(imbalanced_data.shape)
minor_data_arr2, major_data_arr2 = seperate_minor_and_major_data(imbalanced_data)
print(minor_data_arr2.shape)
print(major_data_arr2.shape)
# 测试Border_SMOTE方法
balanced_data_arr2 = Border_SMOTE(imbalanced_data)
print(balanced_data_arr2.shape)
辅助类代码和上面的base_sampler一样,这里就不在累赘了
以上内容有部分是借鉴了网上的资料,本人知识有限,若哪里写的不对,还望各位读者见谅并多多指教!