【论文阅读笔记】——GMNN: Graph Markov Neural Networks

ICML2019《GMNN: Graph Markov Neural Networks》 by Meng Qu, Yoshua Bengio, Jian Tang，GNN工作的又一创新，将统计关系学习（SRL）和图神经网络（GNN）结合，该方法适用于图节点分类、节点关系分类，以及无监督的节点表示学习任务。原文地址：https://arxiv.org/abs/1905.06214v1

引言

现实社会的网络中，实体可以被看做一个个的网络节点（在统计关系学习中记作objects/对象，在图中记作节点/nodes），实体的类别可以被看做网络节点的标签（labels），同时每个节点会存在一系列的属性，我们把它们记作features或attributes。当我们为节点做分类任务时，我们通常会以节点的特征为重心，将特征向量送入分类器做训练，但我们同时要考虑两个点：

1. 邻居节点同质性：相连的节点类别趋近相同
2. 标签依赖关系：某些标签更有可能同时出现。如，篮球和NBA可能会是相邻节点，飞机和牛奶很难产生关系等

传统的关于关系数据建模的方法主要跟从两个工作：统计关系学习SRL（如关系马尔科夫网络等）和图神经网络GNN（如GCN等）。

SRL：统计关系学习，通常利用条件随机场CRF来对节点标签依赖关系进行建模。

• 优点：CRF可以学习到节点标签之间的联合分布。
• 缺点：需要手工定义特征函数进行一系列的线性组合来组成势函数，通常这些特征函数都是启发式的，也就是特征需要人工定义，表达能力有限。再一个，网络中的节点关系结构非常复杂，计算节点标签之间的后验分布十分困难。

GNN: 图神经网络通过非线性的神经元架构来学习到节点的特征表示，整个网络进行端到端的分类，目前的GCN和GAT两个主要模型都达到了非常好的效果。

• 优点：强大的特征表达能力，考虑到网络节点的邻接关系。
• 缺点：忽略了标签之间的依赖关系，训练时将节点标签独立地进行预测。

作者由此提出GMNN：Graph Markov Neural Networks，将两者的优点结合在一起：利用CRF学习标签的联合分布，通过伪似然变分pseudolikelihood variational EM算法进行更新迭代：

• M-step：通过GNN学习节点的特征表示，得到更新后的的参数来最大化pseudolikelihood；
• E-step：对节点标签的局部条件分布进行建模，推断未标注节点的标签。

问题

考虑半监督学习中的一个图G=（V,E,x_V），其中V是节点（srl中记作对象）的结合，E是节点之间边的集合，x_V是所有节点属性的集合（可以理解为节点不同维度的特征）。已知一部分标签y_L，L∈V，我们的任务是预测剩下未知的标签y_U，U = V \ L。

方法

SRL
大多使用CRF进行对象标签预测的SRL方法采用公式：
ψ是边上的势函数，一般是人工定义的特征函数的线性组合。
这种情况下，预测未知标签任务被看做是推断问题，我们还要去计算位置标签的后验分布p(y_U|y_L,x_V)，然而由于标签的复杂结构关系，后验十分难求。

GNN
与SRL相比，GNN忽略掉标签的依赖关系，只关注于节点的特征表示。由于GNN将标签之间视为独立，那么此情况下标签的联合分布表示为：
因此，GNN独立地去预测每一个标签：
其中h是|V|×d维的特征向量，W是权重，每一轮节点特征h都会通过自己的邻居进行更新。经过多层网络的学习，特征最后经过一个softmax分类器来预测最终的结果。整个工作可以看做一个端到端的训练。代表性的方法有GCN\GAT。

使用GMNN做半监督节点分类
GMNN利用CRF通过对象属性（节点特征）来建模标签之间的联合分布：p(y_V|x_V)，使用pseudolikelihood variational EM算法进行优化。其中，E-step中使用一个GNN来学习节点的特征表示以预测标签属性，M-step中使用另一个GNN来建模标签之间的依赖关系。

具体来看：

我们沿用CRF的预测模型：p_φ(y_V|x_V)，其中φ是模型参数，我们要做的是优化这个参数来求已知标签的最大似然：p_φ(y_L|x_V)。由于存在大量的未知标签，直接最大化对数似然很困难，因此我们来最大化对数似然的下界（ELBO）:

参考EM算法：
图片来源：https://www.cnblogs.com/vincentbnu/p/9503284.html

上式可以理解为：我们要预测的是已知特征空间x_V下y_L的分布，其中x_V含参数φ，而同时存在一部分未知标签y_U，含隐变量θ。根据EM算法，我们在E-step(推理) 时会固定p_φ来更新q_θ(y_U|x_V)，实际上就是求一个后验概率p_φ(y_U|y_L,x_V)（详见EM算法推导）。在M-step(学习) 时，固定住q_θ更新p_φ来最大化似然函数：
对参数φ的更新又是一个难题（partition function的原因，但那究竟是什么我就不知道了），所以在为φ做优化时，我们采用伪似然公式来代替（4）的方式：
其中NB(n)是节点n的邻居，由推导得到，等式在p_φ(y_V|x_V)独立时成立。（原文说用伪似然方法在马尔科夫网络里已经很实用了，没有做过多解释）

先看推理部分E
这一步的目标是去计算后验概率p_φ(y_U|y_L,x_V)。前文已经说了，由于标签之间的结构十分复杂，隐变量的后验概率很难通过贝叶斯公式求解，所以我们选择使用变分推断，即“使用已知简单分布来逼近需要推断的复杂分布，并通过限制近似分布的类型，从而得到一种局部最优，但具有确定解的近似后验分布”，来代替原来的后验分布。

这里引入mean-field method 平均场理论：平均场假设复杂的多变量Z可拆分为一系列相互独立的多变量Zi，i=1,⋯,M，且q分布可以因子化为这些多变量集的乘积：
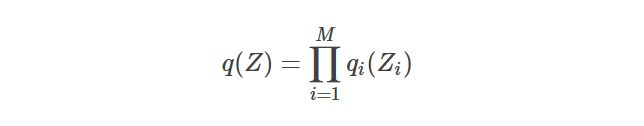于是q_θ可以表示为：
n表示未知标签对象的索引，这里假设所有标签是独立的。我们用GNN来参数化这个q_θ(y_n|x_V)，由此学习到节点的表达：
GNN通过对节点特征x_V建模学习到了特征表示h_θ（可以简单看做|x_V|维的特征空间，θ是特征参数），GNN的好处就是可以学习到周围节点的特征进而丰富自己的特征表达。
论文在附录证明了根据平均场理论，q_θ(y_n|x_V)可以表达为：
右式是其实在对p_φ求期望。我们用采样来代替期望：
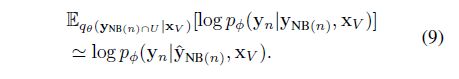其中y^{^}_NB(n) 是从节点n的邻居中采样的点，如果该采样节点k是未标注的，那么y^{^}_k服从q_θ(y_k|x_V)，如果节点k是已知标签的，那么直接采用其真实值。其实验证明在这一步只用采样一个邻居就可以达到不错的效果。根据(8)(9)式我们可以得到：
现在我们假设已经知道在上一个E步中得到的θ，那么θ就可以带到M步中去学习到p_φ(y_V|y^{^}_NB(n),x_V)，此时学习到的p_φ正是我们在当前M步中要去逼近的目标，我们的目标就是最小化q_θ(y_n|x_V)和p_φ(y_n| y^{^}_NB(n),X_V) 的kl散度：KL(p_φ||q_θ)：
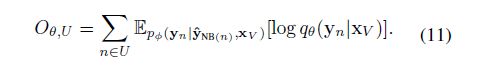另外作者提出，θ也可以用已知标签进行训练，所以可以将y的真实标签带入进去来最大似然估计：
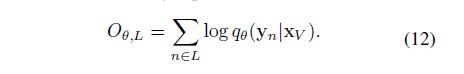最后我们将两部分结合起来就是E-step要去更新的目标：

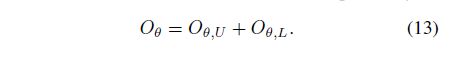
现在来看学习部分M
在学习步骤中我们会固定住E-step得到的q_θ来更新p_φ，进而最大化公式(5)。其实根据上文的内容我们可以看到，p_φ(y_n| y^{^}_NB(n),X_V) 在E和M过程中都会用到（见(5)和(11)），因此我们简化p_φ中的联合分布，将它改成条件分布（我理解其实就是(4)式到(5)式的过程），然后我们再用另一个GNN来参数化它：
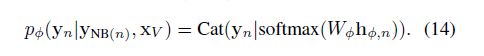我们将这个GNN记作GNN_φ，由公式可以看出来，GNN_φ将y_n的邻居也视作特征进行训练，因此GNN_φ可以建模标签多的局部依赖关系。我们通过训练GNN_φ来优化φ使p_φ最大，所以M步的目标函数为：

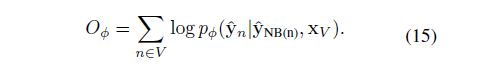
优化过程

使用有标签节点按公式(11)，来预训练q_θ；
交替迭代训练p_φ和q_θ直至收敛；
事实上p_φ和q_θ都可以用来作为最后的标签预测，但实践中q_θ的预测效果总是会很好，所以这里选择使用q_θ来预测最后的输出。算法如图：

应用

除了上述的节点分类任务，GMNN适用于：

无监督节点表示学习
由于节点没有标签，我们的任务看作是为每个节点预测他的邻居节点，此时邻居节点作为伪标签，同时，所有未知标签看作隐变量。

边分类问题
给定部分有标签节点，GMNN可以为边进行分类。
我们为原始图G构造对偶图G’，我们将对偶图中的边集E’视作‘对象’，两条边E’1E’2如果相连，那么它们在原图G中的对应两边E是共享一个节点的。

未完待续