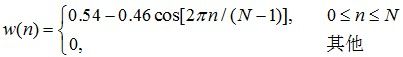语音特征提取方法-MFCC

在深度学习的路上，从头开始了解一下各项技术。本人是DL小白，连续记录我自己看的一些东西，大家可以互相交流。

本文参考：https://blog.csdn.net/u013378306/article/details/65954965 (MFCC)

https://zhuanlan.zhihu.com/p/19763358(傅立叶变换理解)

https://blog.csdn.net/xiaoding133/article/details/8106672(预处理)

零、补充内容

基础知识

音素(phoneme)：是语音中最小的单位。构成单词发音的组成部分，任何一个语言，音素集都一样。

音节(syllable)：音节是听觉能感觉的最直接的语音单位，音节由一个或者多个音素按照一定规律组成的最小的语音结构单位。音节，开头结尾能量最低，两个音节的边界线处能量最低。

音子(phone)：语音识别建模的单位。

提取过程

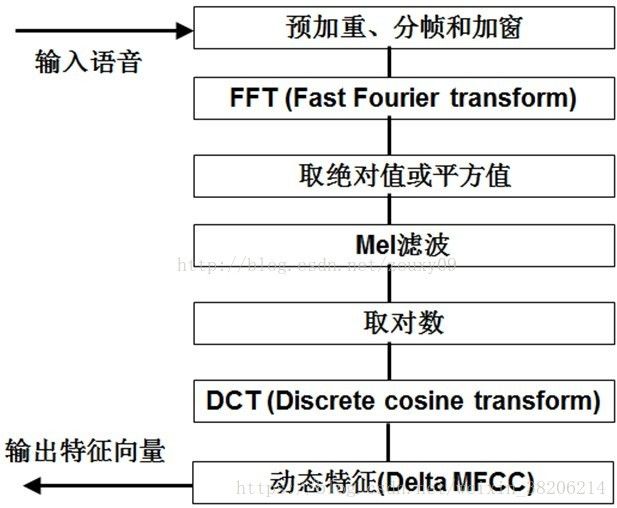
基本步骤

一、预加重

为什么要预加重？

对于语音信号来说，语音的低频段能量较大，能量主要分布在低频段，语音的功率谱密度随频率的增高而下降，这样，高频段的输出信噪比明显下降，从而导致高频段传输衰弱，使高频段传输困难，影响信号的质量。预加重的目的是提升高频部分，使信号的频谱变得平坦，保持在低频到高频的整个频带中，能用同样的信噪比求频谱。同时，也是为了消除发生过程中声带和嘴唇的效应，来补偿语音信号受到发音系统所抑制的高频部分，也为了突出高频的共振峰。

声门气流波每倍频音下降12dB，唇腔辐射每倍频音提升6dB，合起来语音每倍频音下降6dB，采用预加重对高频提升，尽量使得频谱平坦。

处理过程，其实是将语音信号通过一个高通滤波器：

其中值介于0.9到1.0之间，通常取0.97.

二、分帧

分帧和加窗实际上是一个连续的操作。在生活中，声音一般是非平稳信号，其统计特征不是固定不变的，但是在一段时间内，可以认为信号是平稳的，即短时平稳性（10--30ms内可以认为语音信号近似不变）。这样就可以把语音信号分为一些短段来进行处理，即为分帧。语音信号的分帧是采用可移动的有限长度的窗口进行加权的方法来实现的。

先将N个采样点集合成一个观测单位，称为帧。通常情况下N的值为256或512，涵盖的时间约为20~30ms左右(每秒的帧数约为33~100帧)。为了避免相邻两帧的变化过大，因此会让两相邻帧之间有一段重叠区域，此重叠区域包含了M个取样点，通常M的值约为N的1/2或1/3。通常语音识别所采用语音信号的采样频率为8KHz或16KHz，以8KHz来说，若帧长度为256个采样点，则对应的时间长度是256/8000 1000=32ms。

PS.采样频率选定

Nyquist 定理:如果想要从数字信号无损转到模拟信号，我们需要以最高信号频率的 2 倍的采样频率进行采样。通常人的声音的频率大概在 3kHz~4kHz, 因此语音识别通常使用 8k 或者 16k 的 wav 提取特征。16kHz 采样率的音频，傅里叶变换之后的频率范围为 0-8KHz。

三、加窗

因为我们的计算机只能处理有限长度的信号，因此原始信号X(t)要以T（采样时间）截断，即分帧，成为XT(t)后再进一步处理，这个过程序就是加窗处理。我们将每一帧乘以汉明窗[见PS]，增加帧左侧和右侧的连续性，即为加窗。

加窗之后是为了进行傅里叶展开，所以加窗的目的大致如下：

1. 使全局更加连续，避免出现吉布斯效应[见PS]。
2. 加窗之后，原本没有周期性的语音信号呈现出周期函数的部分特征。

假设分帧后的信号为S(n)，n = 0, 1..., N-1。N为帧的大小。汉明窗为W(n)，公式如下：

其中W(n)的形式如下：

其中a为汉明窗的参数，一般情况下取0.46，即：

窗由3个参数来描述：窗长（单位毫秒），偏移和形状。每一个加窗的声音信号叫做一帧，每一帧的毫秒数叫做帧长，相邻两帧左边界(右边界)的距离叫帧移。时间是25ms，重叠15ms。

PS.吉布斯(Gibbs)现象：

将具有不连续点的周期函数（如矩形脉冲)进行傅立叶级数展开后，选取有限项进行合成。当选取的项数越多，在所合成的波形中出现的峰起越靠近原信号的不连续点。当选取的项数很大时，该峰起值趋于一个常数，大约等于总跳变值的9%。吉布斯现象如下图所示。

它的不足之处在于 ：相邻子图像数据在各个边界不连续造成的所谓Gibbs现像。这是由于图像数据的二维付立叶变换实质上是一个二维图像的付立叶展开式。当然这个二维图像应被认为是周期性的。由于子图像的变换系数在边界不连续 ，而将造成复原的子图像在其边界也不连续 。于是由复原子图像构成的整幅复原图像将呈现隐约可见的以子图像尺寸为单位的方块状结构，影响整个图像质量 。当子图像尺寸较小时更为严重。

解决这个Gibbs现象的方法是后来研究出来的二维余弦变换（DCT）代替二维付立叶变换。基本思路为：用一个对称的2N*2N 像素的子图像代替原来N*N 子图像。由于对称性， 子图像作二维付立叶变换，其变换系数将只剩下实数的余弦项。这样，即可消除Gibbs现象。

PS.窗选择-汉明窗

在平时选择加窗时，我们用得最多的是矩形窗，这个也很容易理解，好像我们屋子里的窗口一样，透过窗口我们可以看到外面的世界，但在如果我们理窗口远一些的话，我们的看到的范围将减少，越远就越小。实际的信号处理过程中，我们如果用矩形窗，矩形窗在边缘处将信号突然截断，窗外时域信息全部消失，导致在频域增加了频率分量的现象，即频谱泄漏。避免泄漏的最佳方法是满足整周期采样条件，但实际中是不可能做到的。对于非整周期采样的情况，必须考虑如何减少加窗时造成的泄漏误差，主要的措施是使用合理的加窗函数，使信号截断的锐角钝化，从而使频谱的扩散减到最少。

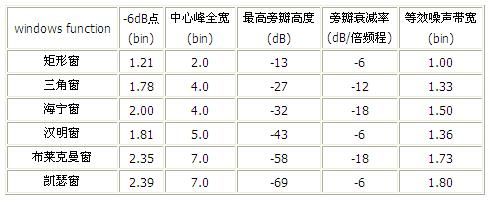
常见的几种窗的基本指标：

一个窗是否合适：窗谱主瓣宽度就尽可能的窄，且能量集中在主瓣内，以获得较陡的过渡带；窗谱旁瓣与主瓣相比应尽可能的小，旁瓣能量衰减要快，以利于增加阻带衰耗。

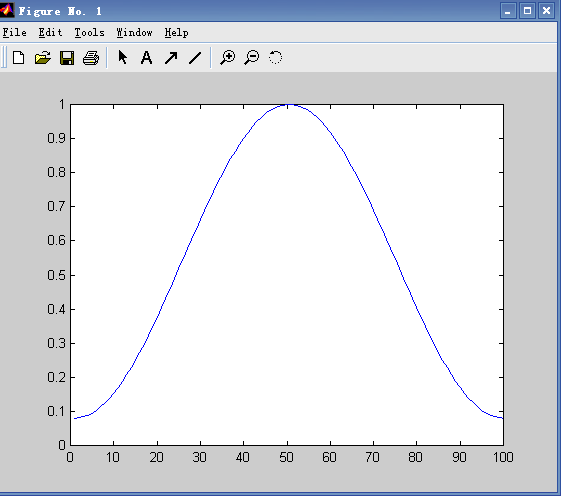
汉明窗(Hanmming)，图像如下：

主要部分的形状像sin(x)在o到pi区间的形状，其余部分为0。汉明窗乘上其他的任何函数f， f只有一部分有非0值。即只有中间的数据体现出来，两边的数据信息丢失，所有移窗的时候，只会移1/3或1/2窗，这样被前一帧或二帧丢失的数据又重新得到体现，同时也不会突然截断数据。

MFCC维数

一般我们用到的MFCC有12维、13维(加入F0能量)、39维(13维的MFCC加上13维的一阶导和13维的二阶导)。即39维。
其中，13维静态系数由1维能量系数(F0) + 12维 dct 系数构成，能量系数可以用来区分语音帧和非语音帧，下面分析12 dct系数的提取过程：

N -> 24 (FFT、Mel滤波器)
帧大小为N。首先对一帧信号做短时傅里叶变换，得到能量谱（幅度谱平方），直接将所有频点 （N维）能量作为特征有非常大的冗余，因为听觉掩蔽效应许多相邻频率对人耳作用结果相似，因此通常用少量Mel滤波器将频域划分成少量子带（比如24个Mel滤波器，这些子带在mel频域是均匀划分的，相邻子带有一半重叠，在自然频域则是低频窄高频宽)， 每个子带输出子带能量和作为特征表征该频率段的能量水平，这样就得到24个特征。

24 -> 12(求对数、DCT)
这里首先要对24个子带能量求对数，这也是叫它倒谱系数的原因，我理解这里求对数只是压缩一下动态范围，也可能是模仿人耳对数式感知声强的特点。由于子带有重叠，所以相邻子带能量有一定冗余。通过DCT变换对24个子带能量特征进行去相关并降到13维， 包括C0~C12。(通过离散余弦变换（DCT）而来，DCT的作用是为了获得频谱的倒谱，倒谱的低频分量就是频谱的包络，倒谱的高频分量就是频谱的细节，这些都是语音识别上经过科学验证十分有效的语音物理信息) C0其实就是各个子带的总能量水平，C0和能量系数想要表达的东西是一致的，因此有的实现保留C0不要能量系数，有的实现则相反。主流方式是舍弃C0， 保留C1~C12共12维特征。这里C0-C12即为前13个系数，因为在经过DCT之后，系数会依次递减，在13个之后几乎都为0。 

标准的倒谱参数MFCC只反映了语音参数的静态特性，语音的动态特性可以用这些静态特征的差分谱(求导)来描述。

其中，差分系数用来描述动态特征，也即声学特征在相邻帧间的变化情况。静态mfcc假设帧与帧之间相互独立，这与实际情况未必符合，比如浊音时相邻帧之间相关程度很高，对应的静态mfcc可能也有较大相关，而动态系数描述了相邻帧的联系，解决了静态mfcc不合理假设可能带来的问题。（极限情况下假设浊音时相邻帧静态mfcc完全相等，则差分系数为零，而清音时差分系数则和静态mfcc幅度相当。这种相邻帧特征的关系通过差分特征得以获取)

一、前言

 

    在任何一个语音识别系统中，第一步就是提取特征，将一段声音转化为计算机可以识别的数字序列或向量。我们需要把音频信号中，具有辨识度的成分提取出来，去除其他不需要的信息，比如背景噪音、情绪等等。

    MFCC（Mel frequency Cepstral Coefficients）梅尔频率倒谱系数，是一种在自动语音和说话人识别中广泛使用的特征。1980年，由Davis和Mermelstein提出。

    本文分为两个部分，分别阐述MFCC的理论理解，以及MFCC的提取过程。

二、声谱图(Spectrogram)与频谱图(Spectrum)

 

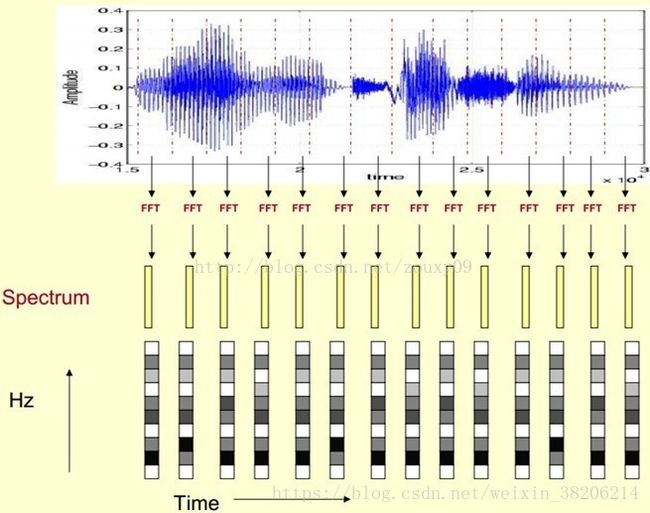
    声谱图是我们用于描述语音信号的一种方式。其中，横轴为时间(Time-s)，竖轴为振幅(Amplitude-dB)。(下图上半部分)

    在声谱图中，我们将横轴时间切分为很多帧，其中每帧语音都对应与一个频谱(通过短时FFT计算)。

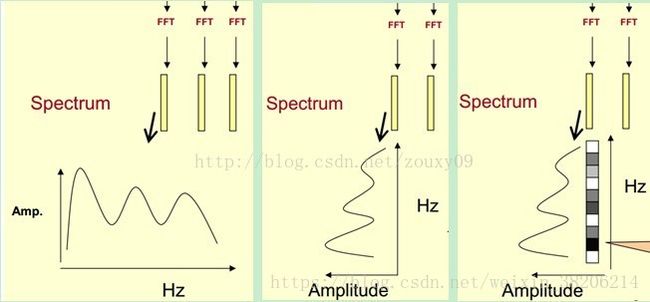
    频谱图，表示频率与能量的关系，横轴为频率(Frequency-Hz)，竖轴为振幅(Amplitude-dB)。(下图左1)

    在对声谱图做FFT计算得到频谱图之后，我们先将其中一帧语音的频谱图通过坐标表示(左1)。我们首先将频谱图逆时针旋转90度，得到左2。然后将振幅映射到一个灰度级表示(可以理解是将连续的振幅量化为256个量化值)。其中0为黑，255为白，振幅越大，对应区域越黑，反之亦然，得到图左3。之后我们将每一帧的频谱图结合，即可得到该声谱图对应的，随时间变化的声谱图(下图)。

 

    该部分由于涉及到FFT变化以及时域到频域的变化，如有难理解的地方，可以了解一下傅立叶变换的逻辑，见链接

https://zhuanlan.zhihu.com/p/19763358

三、倒谱分析(Cepstrum Analysis)

 

    倒谱分析是对频谱图的处理分析过程，其中运用了同态信号处理。它的目的是将非线性问题转化为线性问题的处理方法。原来的语音信号，实际上是一个卷性信号。

    第一步通过卷积将其转换为乘性信号(时域的卷积等于频域的乘积，即从声谱图转变为频谱图)。

    第二步通过取对数，将乘性信号转化为加性信号(运用log的运算性质：logMN = logM + logN)。

    第三步进行逆傅立叶变换，将加性信号恢复为卷性信号。

    接下来，我们对整个倒谱分析做一个具体的解释。

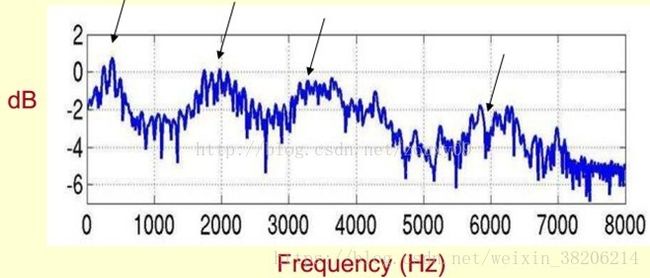
    首先，对于一个语音的频谱图，其峰值就表示语音的主要频率成分，我们将其峰值称为共振峰(formants)，而共振峰就是携带声音辨识属性的元素，对于我们识别不同声音很重要。

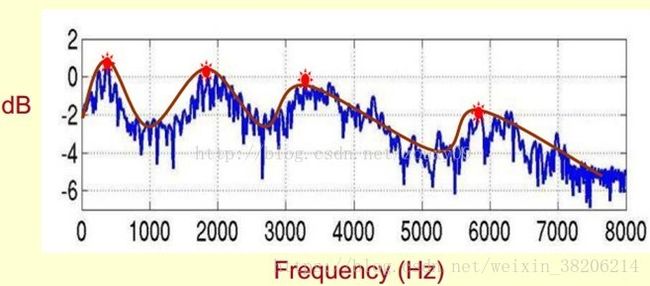
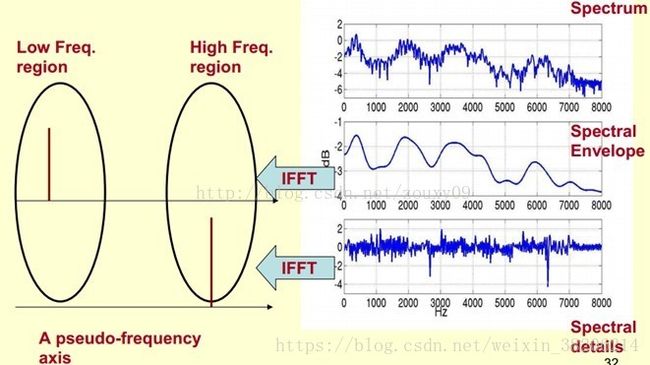
    我们在提取共振峰的时候，不仅仅要提取共振峰的位置，同时还需要提取到它转变的过程，所以我们提取的是频谱的包络(Spectral Envelope)，包络是一条链接这些共振峰点的平滑曲线(下图)。

    

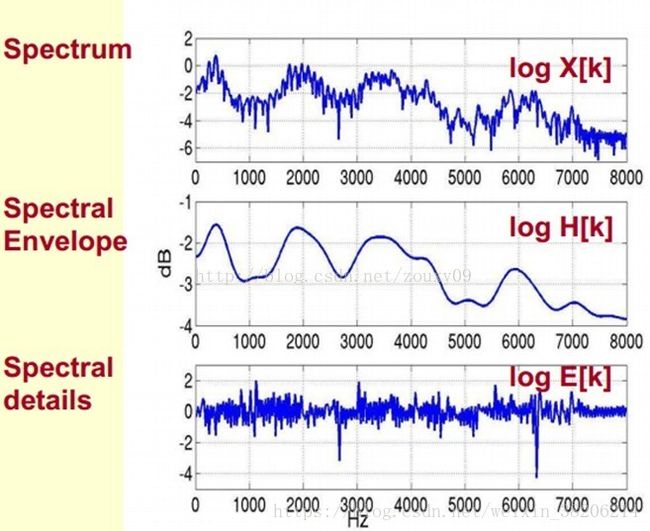
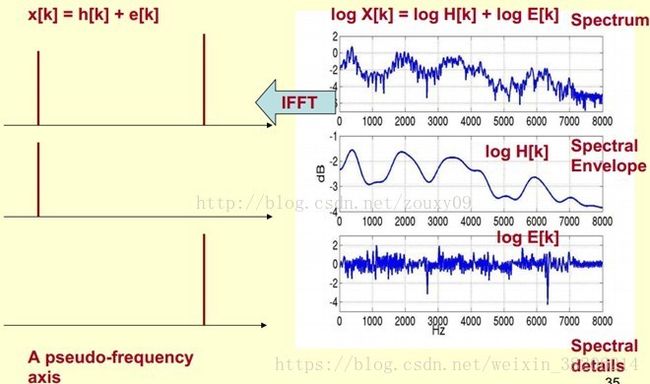
    那么，我们可以理解为，将原始的频谱分为两个部分，包络和频谱的细节(其他部分)。我们将其分开，即得到下图。我们将包络设定为log H[k]，频谱的细节设定为log E[k]。

    其中，我们已知频谱log X[k]，所以我们需要求得log H[k]和log E[k]，使其满足log X[k] = log H[k] + log E[k]。

    接下来，我们需要对频谱做一个数学转化，即为对频谱做FFT。因为我们从声谱图做FFT转化为频谱图，所以对频谱做FFT可以理解是逆傅立叶变换IFFT(Inverse FFT)。

    由下图可见，我们在给频谱做IFFT时，包络主要是低频部分，而频谱的细节部分主要是高谱部分。

    将IFFT逆转之后的部分，叠加起来，即可得到原来的频谱信号。

    在实际运算过程中，我们已知log X[k]，所以可以求得x[k]。由上图可知，x[k]的低频部分是h[k]。将x[k]通过一个低通滤波器就可以获得h[k]。也就是频谱的包络。

    总结下， x[k]实际上就是倒谱(cepstrum)(就是spectrum倒过来)，而我们关心的h[k]就是倒谱的低频部分，描述了频谱的包络，也是语音识别中被广泛应用于描述特征。整个倒谱(cepstrum)就是一种信号的傅立叶变换，经对数运算后，再进行逆傅立叶变换得到的谱，计算过程如下：

公式如下：

 

1）将原语音信号经过傅里叶变换得到频谱：X[k]=H[k]E[k](只考虑幅度就是：|X[k] |=|H[k]||E[k] |)；

2）我们在两边取对数：log||X[k] ||= log ||H[k] ||+ log ||E[k] ||。

3）再在两边取逆傅里叶变换得到：x[k]=h[k]+e[k]。

 四、Mel频率分析(Mel-Frequency Analysis)

 

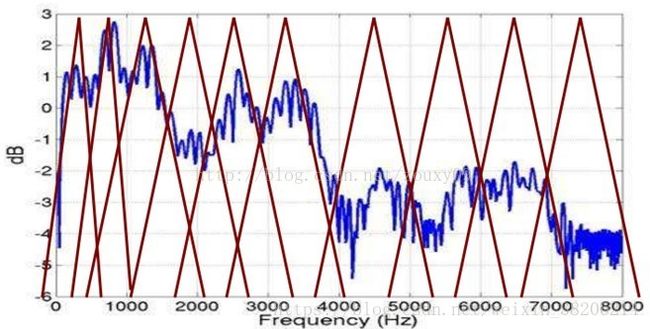
    以上，即为倒谱分析。即我们从一段语音，提出得到它的频谱包络，但是从人类听觉实验表明，人类听觉仅仅聚焦在某些特定的区域，而不是整个频谱包络。根据Mel频率分析，我们发现人耳类似于一个滤波组，只关注特定的频率分量。并且这些滤波器在频率坐标轴上，并不是统一分布的，在低频区域有很多的滤波器，分布比较密集，在高频区域，滤波器的数目会比较少，分布很稀疏(如下图)。

    MFCC(梅尔频率倒谱系数)考虑到了人类听觉特征，过程是先将线性频谱映射到基于听觉感知的Mel非线性频谱中，然后转换到倒谱上。

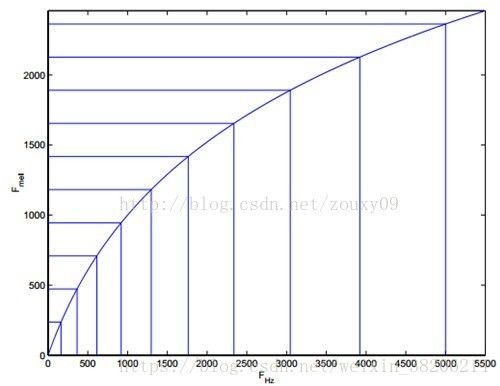
    其中将普通频率转化到Mel频率的公式是：

    

公式图像为：

五、Mel频率倒谱系数(Mel-Frequency Cepstral Coefficients)

    我们将频谱通过一组Mel滤波器就可以得到Mel频谱。其公式表示为：

    log X[k] = log(Mel-Spectrum)

    这时候，我们可以在log X[k]上进行倒谱分析：

1> 取对数：log X[k] = log H[k] + log E[k]

2>进行逆变换: x[k] = h[k] + e[k]

    在Mel频谱上面倒谱分析获得的包络h[k]，就称为Mel频率倒谱系数(MFCC)。

 

总结而言，提取MFCC特征的过程：

1> 先对语音进行预加重、分帧和加窗；

2>对于每一个短时分析窗(即分出的每一帧)，通过FFT得到对应的频谱；

3>将上面计算得到的频谱通过Mel滤波器组，得到Mel频谱；

4>在Mel频谱上进行倒谱分析(取对数、逆变换(见ps))，获得Mel频谱倒谱系数MFCC，这个MFCC就是这帧语音的特征。

ps.在Mel倒谱分析过程中，实际的逆变换一般是通过DCT离散余弦变化。取DCT之后的第2个到第13个系数，作为MFCC系数。

ps.对语音进行预加重、分帧和加窗，实际上是对语音的类似于正则化和分帧的过程，具体可以参考博客

https://blog.csdn.net/xiaoding133/article/details/8106672