主成分分析实例

实例描述

某面馆有各种种类的汤面，为了得知受欢迎程度，进行了在【面】、【汤】、【配料】3个维度的打分。现利用主成分分析法对数据挖掘。

步骤

确定主成分

• 加载包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#中文文字显示问题
from pylab import mpl
# 指定默认字体
mpl.rcParams['font.sans-serif'] = ['FangSong'] 
# 解决保存图像是负号'-'显示为方块的问题
mpl.rcParams['axes.unicode_minus'] = False 

• 读取数据

df_org = pd.read_excel("拉面.xlsx", sheetname="拉面")

• 标准化数据

df_std = (df_org - df_org.mean())/df_org.std()

• 获得相关系数矩阵

df_corr = df_std.corr()

• 计算特征值和特征向量

eig_value,eig_vector=np.linalg.eig(df_corr)
#特征值排序
eig=pd.DataFrame({"eig_value":eig_value})
eig=eig.sort_values(by=["eig_value"], ascending=False) 
#获取累积贡献度
eig["eig_cum"] = (eig["eig_value"]/eig["eig_value"].sum()).cumsum()
#合并入特征向量
eig=eig.merge(pd.DataFrame(eig_vector).T, left_index=True, right_index=True)

• 提取主成分

#假设要求累积贡献度要达到70%，则取2个主成分
#成分得分系数矩阵（因子载荷矩阵法）
loading = eig.iloc[:2,2:].T
loading["vars"]=df_std.columns

计算得分

• 确定分析精度
  从累积贡献度可以看到，前2个主成分的累积贡献度达到了79%，就是本次的分析精度。
• 计算主成分得分
  标准化数据 ·因子载荷矩阵

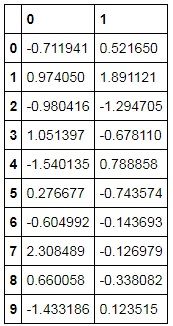
score = pd.DataFrame(np.dot(df_std,loading.iloc[:,0:2]))

解读结果

• 查看变量在新坐标系中的位置。

plt.plot(loading[0],loading[1], "o")
xmin ,xmax = loading[0].min(), loading[0].max()
ymin, ymax = loading[1].min(), loading[1].max()
dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2
plt.xlim(xmin - dx, xmax + dx)
plt.ylim(ymin - dy, ymax + dy)
plt.xlabel('第1主成分')
plt.ylabel('第2主成分')
for x, y,z in zip(loading[0], loading[1], loading["vars"]):
    plt.text(x, y+0.1, z, ha='center', va='bottom', fontsize=13)
plt.grid(True)
plt.show()

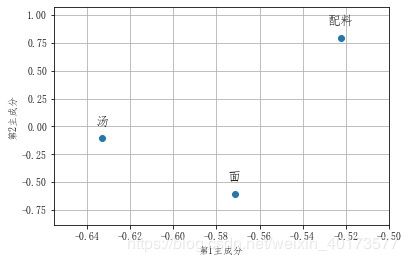
影响力与正负数无关，只看绝对值。
可以看到 变量中【汤】对第1主成分影响较大；【配料】对第2主成分影响略大于【面】。

• 查看每个数据在新坐标系中的位置

plt.plot(score[0],score[1], "o")
xmin ,xmax = score[0].min(), score[0].max()
ymin, ymax = score[1].min(), score[1].max()
dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2
plt.xlim(xmin - dx, xmax + dx)
plt.ylim(ymin - dy, ymax + dy)
plt.xlabel('第1主成分')
plt.ylabel('第2主成分')
for x, y,z in zip(score[0], score[1], score.index):
    plt.text(x, y+0.1, z, ha='center', va='bottom', fontsize=13)
plt.grid(True)
plt.show()

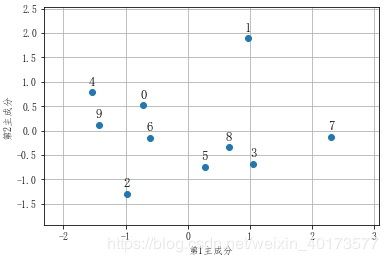
由于第1主成分的所有系数都是负值，所以其得分负向越大，该数据对应的第1主成分得分越高。
可以看到4号数据第1主成分得分最高，说明它的【汤】最受欢迎；同理，1号数据第2主成分得分最高，其【配料】评价最高。

• 备注
  此案例为了表明具体算法过程。实际应用中，可使用被封装的PCA包：

from sklearn.decomposition import PCA