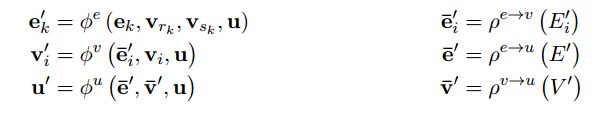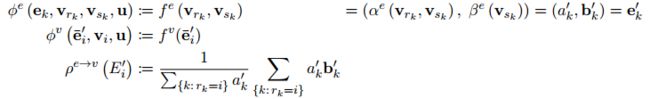图网络模型原理详解(Graph Network)
《Relational inductive biases, deep learning, and graph networks》
这篇论文包含了一部分新研究、一部分回顾和部分统一结论,这篇文章涉及到的很多知识面,涉及到联结主义、行为主义、符号主义,其本身的模型并不难,但是要理解其提出来的背景及相关知识联系,和其研究的深层含义就需要慢慢品读其中的参考文献了。
这篇论文是DeepMind联合谷歌大脑、MIT等机构27位作者发表重磅论文,提出“图网络”(Graph network),将端到端学习与归纳推理相结合,有望解决深度学习无法进行关系推理的问题。
作者认为组合泛化是人工智能实现与人类相似能力的首要任务,而结构化表示和计算是实现这一目标的关键,实现这个目标的关键是结构化的表示数据和计算(structured representation)。本文讨论图网络如何支持关系推理和组合泛化,为更复杂的、可解释的和灵活的推理模式奠定基础。
人类智能的一个关键特征是“无限使用有限方法”的能力,也就是说我们一旦掌握了一种方法,我们可以无限次将这种方法应用到对应的场景中解决对应的问题,比如:我们学习说话并不是将世界上所有的句子都学一遍,我们学习的是单个的单词还有语法,然后我们可以将单词经过特定的语法组织,组成很多很多句子。这反映了组合归纳的原则,即从已知的构建块构造新的推论、预测和行为。人类的组合概括能力主要取决于我们表达结构和推理关系的认知机制。我们将复杂系统表示为实体及其相互作用的组合,比如判断一堆不规则的石头堆砌起来是否稳定。人类的认知可以通过层层抽象来去掉事物间细节上的差异,保留下最一般的共同点;所以我们可以通过组合已有的技能和经验来解决新的问题(例如去一个新地方可以将“坐飞机”、"去圣迭戈"、“吃饭”、“在一家印度餐馆”这几个已有的概念组合起来得以实现。);人类可以将两个关系结构(指的就是graph这种表示物体和物体间关系的数据)放在一起进行比较,然后根据对其中一个的知识,来对另一个进行推断。
当前的深度学习方法都强调end-to-end,端到端的学习方式,而当数据量和计算资源没有现在这么丰富的时候,人们都是采取的hand-engineering的方式,手动设计各种模型。作者认为在这两种模型之间的选择不应该走极端,只要一个而不要另一个,应该是end-to-end和hand-engineering相结合来设计模型。
Relational reasoning
这里我们将 "结构" 定义为一堆已知的构件快的组合,“结构化表示”主要关注组合(即元素的排列),“结构化计算” 作用对象为元素及元素组成的总体,"关系推理" 涉及操纵实体和关系的结构化表示,并使用规则去组合实体和关系。概念如下所示:
实体是具有属性的元素,例如具有大小和质量的物理对象。
关系是实体之间的属性。这里我们关注实体之间的配对关系。
规则是一种函数,它将实体和关系映射到其他实体和关系,这里我们采用一个或两个参数的规则,并返回一元属性值。
Relational inductive biases
首先需要解释一下什么是归纳偏置(Inductive biases)
inductive bias,这个概念顾名思义,就是在归纳推理(induct)的时候的偏向(bias),也就是在模型学习的时候,参数有倾向性的调节成某种状态,模型有倾向性的学习成某一类样子。
学习是通过观察和与世界互动来理解有用知识的过程,这就涉及到从一个有很多解决方案的空间中寻找一个最优的能很好对数据做出解释的解决方案,当我们采用了某个解决方案我们的回报也是最大的。可能在很多场景下,有很多解决方案的效果是相同的,但是 Inductive Bias 会让学习算法不依赖观测数据优先考虑一个最最最优的方法,因为他有偏向啊。在贝叶斯模型中,归纳偏置表现为先验分布模型的选择和参数的选择,在另外一些场景中,偏置项可能表现为防止过拟合的正则化项,或者这个偏置项的存在纯粹就是因为模型本身的结构就是这样要求的。归纳偏置通常牺牲灵活性以提高样本的复杂性。理想情况下,归纳偏置既可以改善对解决方案的搜索,又不会显着降低性能,并有助于找到以理想方式推广的解决方案;然而,不合适的归纳偏置项会引入太强的约束可能导致最终的效果并不是最优的。
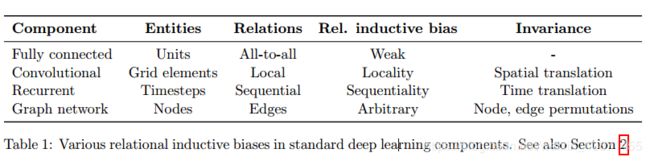
在深度学习中,实体和关系通常表示为分布式表示,规则可以当做是神经网络函数逼近器; 然而,实体,关系和规则的确切形式因架构而异。也就是说不同的网络架构对应到的实体和关系是不同的,CNN对应着自己的实体和关系,RNN同样也对应着他自己的实体和关系,如下图所示:
每种不同的网络模型对应的实体、关系、偏置项都不同,例如RNN中实体代表着时间步,关系代表着序列
标准深度学习模型中的关系归纳偏置
这里需要说relational inductive biases有别于inductive biases,什么区别我们来看模型
全连接层:
输入的是一个向量,输出的是每个向量元素与权重向量点乘之后加上偏置项,经过一个激活函数,例如(ReLU)。在这个网络中,实体是网络中的单元,关系是各个单元连接的权重参数(层i中的所有单元连接到层j中的所有单元),并且规则是由权重和偏差组成的一系列函数来表示。整个模型中没有共享参数,信息之间也没有隔离,每一个单元都可以参与决定任何一个输出单元,和输出是没有关系的。因此,全连接层的relational inductive biases是很弱的,也就是模型并没有在归纳推断的时候偏向于哪个relation,而是一视同仁,每个单元都连接到后一层的单元节点,自由度非常大。
卷积层:
CNN中的实体还是单元,或者说是网格元素(例如image中的pixel),relation更加稀疏。相比于全连接网络,这里加入的relational inductive biases是局域性和平移不变性,局域性指的就是卷积核是大小固定的,就那么大,只抓取那么大的区域的信息,远处的信息不考虑;平移不变性指的是rule的复用,即卷积核到哪里都是一样的,同一个卷积核在各个地方进行卷积。到这我们可以看到,rule在深度学习的模型中的含义是如何将某一层的网络信息传递到下一层,而且是具体到权重的值是多少,后文还提到一句话“learning algorithm which find rules for computing their interactions”,也就是说,算法指的是计算框架,例如卷积操作之类的,而rule是学习到的具体的以什么权重进行卷积操作。
循环神经网络:
RNN中的entity是每一步的输入和hidden state;relation是每一步的hidden state对前一步hidden state和当前输入的依赖。这里的rule是用hidden state和输入更新hidden state的方式。rule是在每一步都复用的,也就是说这里存在一个relational inductive biases是temporal invariance,时间不变性。
Computations over sets and graphs
文章提出set(集合)的概念,集合中的元素是没有顺序的,但是集合中元素的一些特征可以用来指定顺序,比如质量体积等等。因此,用来处理set或graph的深度学习模型应该是在不同的排序方式下都能有同样的结果,也就是对排序不变(invariance to ordering)。
作者强调处理set模型的 relational inductive biases 并不是因为有什么relation的存在,而恰恰是由于缺乏顺序,比如求太阳系的中心位置,就是把各个行星的位置进行求平均,每一个行星都是对称的。如果使用多层感知机(MLP)来处理这个问题,那么就可能需要大量的训练才能训练出一个求平均的函数,因为多层感知机对每一个输入都是按照单独的方式处理,而不是一视同仁的处理所有输入。但是有的时候需要考虑排序,例如计算solar system里每一个planet的运动,要考虑planet两两之间的相互作用。以上这两个例子其实是两个极端,一个是planet之间两两没关系,另一个是两两都有关系,而现实世界的很多模型是处在这两个极端之间的(如下图),即并不是每两个之间都没有联系,但也并不是两两之间都有联系,这也其实就是graph模型,每一个物体只与一部分其它物体进行相互作用。
(a)一个分子结构,其中每个原子表示为对应关系的节点和边(Duvenaud 等,2015)。
(b)一个质量弹簧系统,其中绳索由在图中表示为节点的质量序列定义(Battaglia 等,2016;Chang 等,2017)。
(c)一个 n 主体系统,其中主体是节点,底层图是完全连接的(Battaglia 等,2016 年;Chang 等,2017)。
(d)一个精密的主体系统,其中球和壁是节点,底层图形定义球之间以及球和壁之间的相互作用
(e)一个句子,其中单词对应于树中的叶子,其他节点和边可以由解析器提供。或者,可以使用完全连接的图
(f)一张图像,可以分解成与完全连接图像中的节点相对应的图像块(Santoro 等,2017;Wang 等,2018)
Graph networks
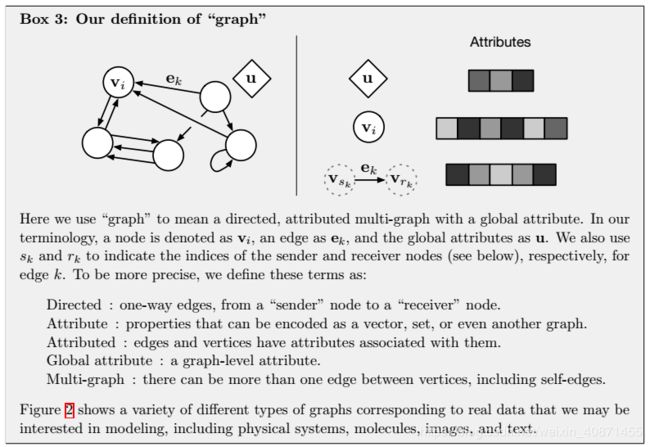
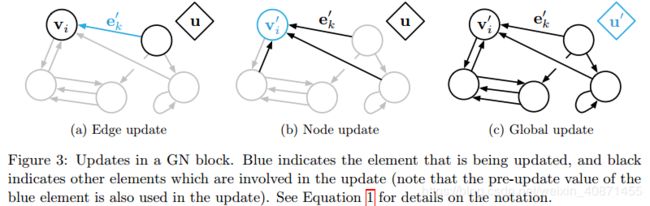
作者在自己的模型中没有使用神经元这个词,意在强调这个模型不一定需要通过neural network实现,也可以使用别的函数。graph network的主要计算单元是GN block,GN block是一个输入输出都是graph的graph-to-graph module。在graph中,前面说过的entity就被表示成节点(node),而relation被表示成边(edge),系统层面的特征用global attribute表示。
节点表示为 v_i,边表示为 e_k,全局属性表示为 u。我们还使用 s_k 和 r_k 分别表示边 k 发送节点和接收节点的索引。
- 有向边:单向边,从「发送」节点到「接收」节点。
- 属性:可以编码为向量、集合甚至其他图形的属性。
- 属性化:边和顶点具有与其关联的属性。
- 全局属性:图级属性。
- 多图:顶点之间可以有多个边,包括自边(self-edge)
graph用一个3元组(3-tuple)表示 G = (u; V; E) (u v e 详见上图)u代表的是一个全局信息(global attribute),是整个graph的一个特征;V代表graph的节点的集合![]() ,E代表边的集合
,E代表边的集合![]() ,
,![]() 、
、![]() 代表边和节点的数量,
代表边和节点的数量,![]() 是第k个边的特征(attribute),
是第k个边的特征(attribute),![]() 、
、![]() 分别是receiver node和sender node的编号
分别是receiver node和sender node的编号
计算单元:GN block 包含三个更新函数和三个聚合函数
左边φ为更新函数,右边ρ为聚合函数
![]() 是作用于edge的,更新第k个edge的时候,输入参数为 [ 当前的特征
是作用于edge的,更新第k个edge的时候,输入参数为 [ 当前的特征![]() 、连接在这个edge两端的节点的特征
、连接在这个edge两端的节点的特征![]() ,以及全局的特征u ] 。
,以及全局的特征u ] 。![]() 是对node使用的,输入的是全局的特征u、当前节点的特征
是对node使用的,输入的是全局的特征u、当前节点的特征![]() 、以及
、以及![]() , 这个
, 这个![]() 是由公式第一行右边的aggregation function来得到的。
是由公式第一行右边的aggregation function来得到的。![]() 是用来更新全局信息的,输入也无需赘述。
是用来更新全局信息的,输入也无需赘述。
右边的三个函数,每一个函数都有一个上标,这个上标指的是由什么的信息生成什么的信息,例如![]() 指的是由edge的信息生成node的信息。这三个函数的输入:
指的是由edge的信息生成node的信息。这三个函数的输入:
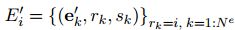 ,这里,rk=i,即所有指向索引为i的节点的有向边,可以看出将要生成的是第i个node的信息,
,这里,rk=i,即所有指向索引为i的节点的有向边,可以看出将要生成的是第i个node的信息,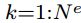 指的是所有的edge,这个函数也就是用所有更新过的edge的信息来生成一个用来产生新的node信息的
指的是所有的edge,这个函数也就是用所有更新过的edge的信息来生成一个用来产生新的node信息的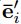 ,然后再由
,然后再由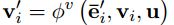 生成最终的新的node信息。
生成最终的新的node信息。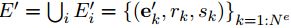
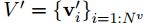
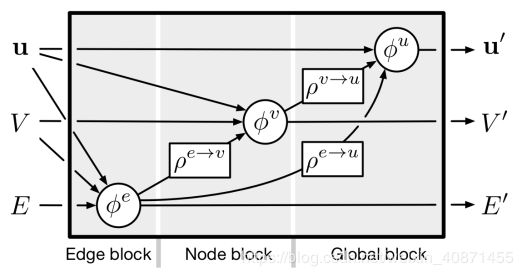
右边的函数解释通了,左边的函数中的输入变量也就有了,也就是说,整个过程是:
- 首先用当前的edge信息、node信息、以及全局信息u来生成新的edge的信息,
- 有了新的edge信息,就能生成新的node信息;
- 有了新的node和edge信息,就能生成新的全局信息u,整个更新过程也就完成了。
算法的过程如下图:
这个算法,输入是graph的三个组成部分:node、edge、u。
- 函数在第一个循环中用更新edge的update function更新每一个edge,
- 在第二个循环中,更新每个node的特征,
- 然后生成
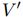 、
、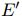 ,将这两个参数分别进行聚合生成相应的信息
,将这两个参数分别进行聚合生成相应的信息 、
、 ,
, - 最后更新u,
- 函数最后的返回值就是更新后的edge、node、u。
算法计算步骤示意图如下:
这里面,作者强调,函数![]() 的输入是一个集合,输出是一个单独的值,这个函数要能做到可以输入不同数量的元素,也就是说输入集合的大小是可变的,而且,输入集合中的元素无论怎么排列,
的输入是一个集合,输出是一个单独的值,这个函数要能做到可以输入不同数量的元素,也就是说输入集合的大小是可变的,而且,输入集合中的元素无论怎么排列,![]() 都应该输出同样的信息。即invariant to permutation。这个更新的顺序作者认为不是固定的,倒过来先更新global,再更新node,再更新edge也是无所谓的
都应该输出同样的信息。即invariant to permutation。这个更新的顺序作者认为不是固定的,倒过来先更新global,再更新node,再更新edge也是无所谓的
作者给了一个具体的例子来使这个更新过程更加具体,假定我们有一个系统,是由橡胶球以及球体之间相连接的弹簧(并不是任意两个球体之间都有弹簧,而是有些球体之间有弹簧,有些没有)构成。第一步update edge的信息可理解为计算和更新球体两两之间的作用力或者弹性势能之类的量;更新node信息可以理解为是根据这些更新好的势能或作用力等表征相互作用的量来更新球体的位置速度等信息;最后更新全局的信息可能是在计算总势能之类的全局量。在这个例子里,先更新哪个都不重要。
Relational inductive biases in graph networks
GN block的relational inductive biases是很强的
首先,每一个输入的graph的entity之间的relation都是不一定什么样的,也就是说GN的输入决定了实体节点之间是如何相互作用或者相互独立的;两个entity之间有直接的联系,就用一个edge连接以表示;没有直接的联系,就没有相应的edge,这两个entity之间也就不能直接相互作用。有些时候人们并不会因为graph的两个node之间没有连接而不去让他们直接发生相互作用,例如在一篇人体动作识别的paper中,作者将人体关节两两之间都加上edge,来判断动作,这是因为有些关节之间虽然不是生理结构上直接相连的,但是组合起来却能完成一些动作,例如两个手拍手,这也就体现一个问题,graph中原有的edge并不一定体现我们在计算时所需要的相互作用,或者不全面,人体关节是否直接相连跟他们能否共同完成某些动作并不是唯一的决定性的关系,有很多不相邻的关节其实在我们识别动作时应该设置上相互作用的,比如两只手。
relational inductive biases的第二点表现是graph将entity和entity之间的relation都用set(集合)来表示,这意味着GN对这些元素的顺序的改变要具有不变性。
第三点更新graph的edge和node的函数是在所有的node和edge上复用的,这说明GN会自动支持组合泛化,这是因为无论graph有多少node,node之间的连接是怎样的,GN都能够处理
Design principles for graph network architectures
作者在这里强调,GN是不对attribute representation和函数的形式有什么限制的,但是本文会主要将注意力集中在深度学习的架构上,使得GN成为一个可学习的graph-to-graph的函数近似(function approximator,这个应该是指神经网络都是起到拟合函数的作用,因此训练出来的也就是一个函数的近似)。
Flexible representations
GN对graph representation的支持是很灵活的,一方面是global、edge、node的特征的表示都很灵活,可以是向量、tensor、sequence、set,甚至是graph。为了能和其他的深度学习结构对接,往往会将representation选为tensor或vector。此外,对于不同任务的不同需求,GN都能满足,edge-focused GN就输出edge,例如判断entity之间相互作用的任务;node-focused的就输出node,graph-focused的就输出global。另一方面,GN对输入graph的结构也没要求,什么结构都支持。我们得到的数据可能是entity之间所有的relation都已知的,也可能是都未知的,更多的时候介于这两个极端之间。有的时候,entity是怎么设定的也不知道,这时候可能需要假设,例如将句子中的每个词汇都视作一个node(entity)。relation不明确的时候,最简单的方法是假设所有entity之间都有联系,但这种方法在entity数量很大时不太好,因为这时edge数量随node数量平方增长。因此,relation缺失的问题,也就是从没结构的数据中推测出一些稀疏的结构,也是一个很重要的未来研究的方向
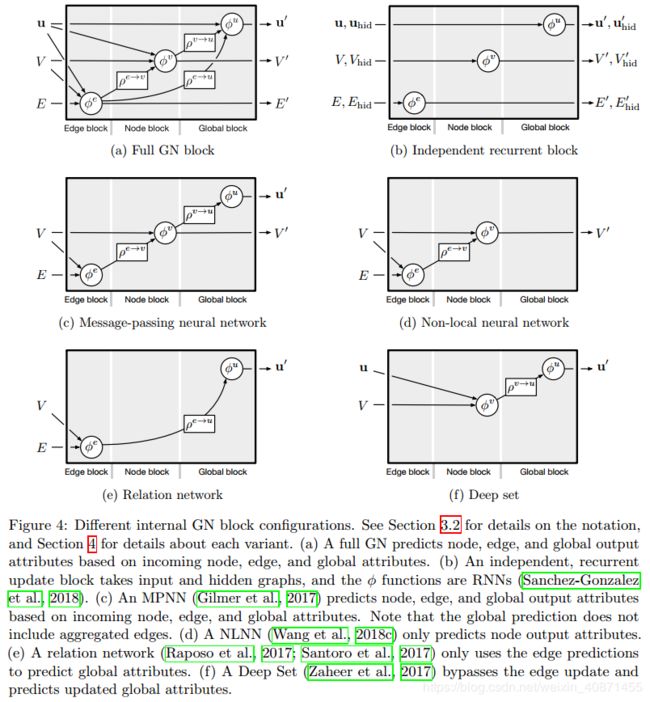
Configurable within-block structure
GN block内部的结构是可以随意改变的,前面介绍了完整的GN block的工作过程,介绍了里面的信息的传输和使用的函数(函数未指定具体形式),但实际应用中,信息的传递结构和函数都可以随意指定,下图给出了几种形式:
(a)是一个完整的GN block,其余的是变种。
(b)是函数![]() 设置为RNN的简单的例子,需要额外提供一个hidden state作为输入和输出。这里面没有message-passing,意思是u、v、e之间没有交流,message-passing应该是特指有graph结构的数据的结点等元素之间按照自己的结构进行信息的传递,例如卷积操作,所以这种没有利用结构信息的就算是没有message-passing了。这种使用RNN的GN block可以用来做一些dynamic graph states的smoothing
设置为RNN的简单的例子,需要额外提供一个hidden state作为输入和输出。这里面没有message-passing,意思是u、v、e之间没有交流,message-passing应该是特指有graph结构的数据的结点等元素之间按照自己的结构进行信息的传递,例如卷积操作,所以这种没有利用结构信息的就算是没有message-passing了。这种使用RNN的GN block可以用来做一些dynamic graph states的smoothing
(c)是2017年Glimer提出的MPNN模型,
(d) NLNN,Non-local neural network,是2018年CVPR的一篇文章提出的,这篇文章提出了各种不同的attention机制,包括intra-/self-/vertex-/graph-attention,这些attention的意思都是指的node如何进行更新。
NLNN模型是不考虑edge的,每两个node之间都会计算一个attention weight,然后加权求和(这也是为什么叫non-local,并不是局部进行卷积,而是全局进行加权),但是一些其他和NLNN类似的工作是只计算有edge相连的节点间的attention weights的,包括Attentional multi-agent predictive modeling(Hoshen 2017)和Graph attention networks。上图其实是将图(d)的![]() 拆解开了,每次计算的时候,
拆解开了,每次计算的时候,![]() 是一个未经过归一化的权重系数,是一个标量,然后
是一个未经过归一化的权重系数,是一个标量,然后![]() 是一个vector,是等待进行加权求和的node的特征经过函数β处理得到的,然后进行卷积的时候就如下述公式进行操作:
是一个vector,是等待进行加权求和的node的特征经过函数β处理得到的,然后进行卷积的时候就如下述公式进行操作:
这三个公式的顺序应该是1、3、2,也就是先更新了edge,然后![]() 是计算了加权求和的结果,最后
是计算了加权求和的结果,最后![]() 用加权求和的结果更新了node。2017年Vaswani(Attention Is All You Need)提出了multi-head self-attention机制,可以并行的同时计算多个attention函数,也就是分别按照不同的权重将近邻节点加权求和,然后将不同权重得到的结果连接起来作为卷积后的结果。这就像是使用了不同类型的edge,通过不同的连接方式进行了卷积。
用加权求和的结果更新了node。2017年Vaswani(Attention Is All You Need)提出了multi-head self-attention机制,可以并行的同时计算多个attention函数,也就是分别按照不同的权重将近邻节点加权求和,然后将不同权重得到的结果连接起来作为卷积后的结果。这就像是使用了不同类型的edge,通过不同的连接方式进行了卷积。
接着作者简介一些其他的GN的变种,指出了完整的GN的各个部分根据需要都可以忽略,有的模型忽略了global信息,有的却只需要global信息,不需要的,就算得到了也直接忽略就好。在输入的时候,如果有的信息没有,比如没有edge信息,那么就当成attribute vector的长度为0即可。
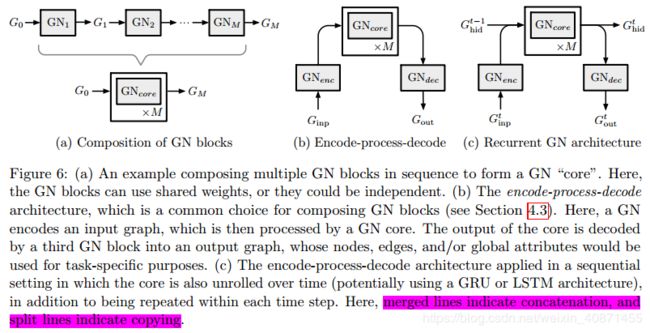
Composable multi-block architectures
设计graph networks的一个关键原则就是通过将GN block组合起来得到复杂的结构。因为GN block输出和输入一样都是graph,因此内部结构不同的GN block也可以方便的组合起来,就像标准的deep learning模型输入输出都是tensor一样。不同的GN block组合起来可以复用内部的函数,就像展开的RNN一样,并且在合并input graph和hidden state的时候,可以采用LSTM或者GRU一样的gating机制,而不是简单地合并起来。
图网络通过组合多个GN模块实现复杂结构,组合形式:
基本的两个GN block的合并方式为![]() 具体公式为:
具体公式为:![]() 一个图G经过GN1的运算的输出作为GN2的输入。
一个图G经过GN1的运算的输出作为GN2的输入。
在上图(a)中,GN block可以是共享的(GN1 = GN2 = · · · = GNM)也可以是不共享的(GN1 ≠ GN2 ≠ · · · ≠ GNM)
(b)中是encoder-decoder模型,这是一种常用方式,将图![]() 输入
输入![]() 进行编码获取到中间隐状态表示
进行编码获取到中间隐状态表示![]() ,输入GNcore中GNcore是一个共享block ,然后解码到输出图。在我们上文提到的小球弹簧系统中,可以这样理解,encoder是计算小球之间初始力和相互作用的能量,core可以理解为一个对系统的动态更新,解码器用于读取系统最终的状态,小球的位置等
,输入GNcore中GNcore是一个共享block ,然后解码到输出图。在我们上文提到的小球弹簧系统中,可以这样理解,encoder是计算小球之间初始力和相互作用的能量,core可以理解为一个对系统的动态更新,解码器用于读取系统最终的状态,小球的位置等
(c)recurrent GN-based architectures类似于RNN,加入了隐藏变量![]() ,这种结构适用于预测图序列,比如动态系统在时间序列下的状态轨迹。经过
,这种结构适用于预测图序列,比如动态系统在时间序列下的状态轨迹。经过![]() 编码后的图必须和
编码后的图必须和![]() 结构一致,这样他们才可以连接他们的
结构一致,这样他们才可以连接他们的![]() 和u向量,在输出的时候
和u向量,在输出的时候![]() 复制一份给
复制一份给![]() 然后进行解码输出。
然后进行解码输出。![]() 在每一步都是共享的
在每一步都是共享的
如果我们不包含全局信息u,那么某个节点的信息需要m个传播步骤后才能到达另一个我们想到达的节点,所以在不带全局信息情况下,节点可以传播的信息由最多m跳的节点和边缘集确定
一些关于graph networks编程的问题,由于node和edge的update function都是在所有node和edge复用的,因此它们的更新都是可以并行计算的;此外,多个graph可以看成一个大的graph的不相连的子图,也可以并行起来计算。
Discussion
首先讨论一下graph networks的combinatorial generalization,作者说道,GN的结构很自然的会支持组合泛化,因为计算不是在整个系统的宏观层面执行的,计算是在各个entity和relation上复用的,这使得之前从来没见过的系统也能够进行处理
接着分析了一些GN的局限性,一方面是有些问题无法解决,像是区分一些非同构的graph之类的问题,另一方面是有些问题不能直接用graph来表示,像一些recursion、control flow、conditional iteration之类的概念至少需要一些额外的假设
深度学习模型可以直接处理原始的感受器得到的信息,但是GN需要的graph如何生成也是个问题,将得到的image,text搞成全连接的graph不是很好,而且直接将这些原始数据的基本元素视作entity也不见得合适,例如参与卷积的像素点并不是图片中的物体,而且实际物体之间的relation可能是稀疏的,如何获取这个稀疏性也是一个问题。因此,能够从原始数据中提取出entity是一个重要的问题
另一个存在的问题是,在计算的过程中,graph也可能发生变化,例如某一个entity代表的物体可能会破碎,那么代表这个物体的node也应该相应的分离开来,类似的,有些时候物体之间的关系也会发生变化,需要添加或者去除edge,这种适应性的问题也正在被研究,现在已经有一些识别graph的underlying structure(潜在的结构)的算法可能是可以用来进行这个任务的。
由于GN的行为和人类对世界的理解类似,都是将世界解释成物体和相互关系组成的,因此GN的行为可能会更加容易解释,变得更加易于分析,更容易可视化。探索GN的可解释性也是未来一个有趣的方向。
虽然本文是将注意力集中在graph上的,但是与此相关的一个方向便是将deep learning和structured representation相结合,相关的工作有很多
参考:https://blog.csdn.net/b224618/article/details/81380567