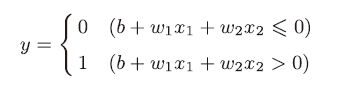深度学习入门(一)：神经网络的起源算法--朴素感知机

本文为《深度学习入门 基于Python的理论与实现》的部分读书笔记
代码以及图片均参考此书

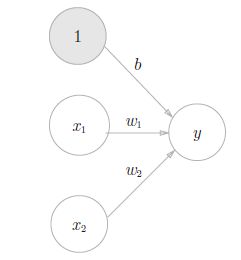
感知机(perceptron)是什么

• b 称为偏置，w1 和w2 称为权重

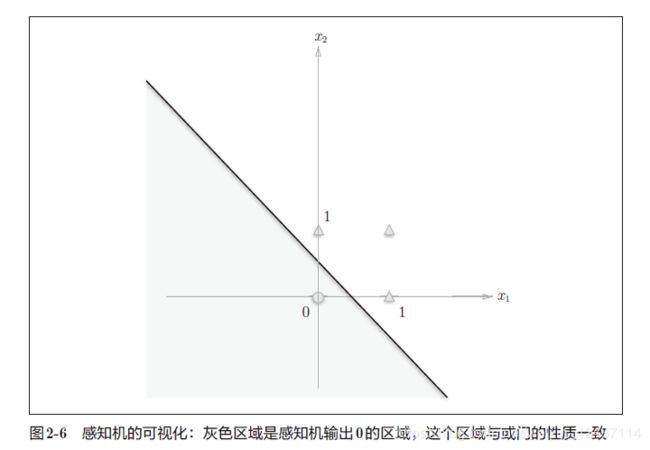
利用感知机实现与门，与非门以及或门

import numpy as np

def perceptron(x, w, b):
    val = np.sum(x * w) + b
    return 0 if val <= 0 else 1

# 这里使用装饰器来测试各种门，在原有的门的基础上进行一些打印输出(其实是小题大做，只是我想练习一下装饰器的用法-_-)
# 不熟悉python的话直接无视即可
def test_gate(test = False):
    def decorator(gate):
        def wrapper(*args, **kargs):
            if test == True:
                print(gate.__name__, ':')
                for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
                    y = gate(xs[0], xs[1])
                    print(str(xs) + " -> " + str(y))
            return gate(*args, **kargs)     
        return wrapper
    return decorator

@test_gate(True)
def and_gate(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    return perceptron(x, w, -0.75)

@test_gate(True)
def nand_gate(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    return perceptron(x, w, 0.75)

@test_gate(True)
def or_gate(x1, x2):
    x = np.array([x1, x2])
    w = np.array([1, 1])
    return perceptron(x, w, -0.5)

if __name__ == '__main__':
    and_gate(0, 0)
    nand_gate(0, 0)
    or_gate(0, 0)

代码输出：

and_gate :
(0, 0) -> 0
(1, 0) -> 0
(0, 1) -> 0
(1, 1) -> 1
nand_gate :
(0, 0) -> 1
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 0
or_gate :
(0, 0) -> 0
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 1

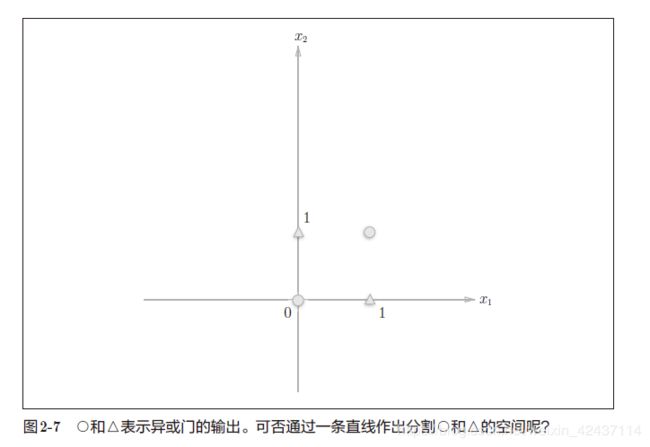
利用感知机实现异或门

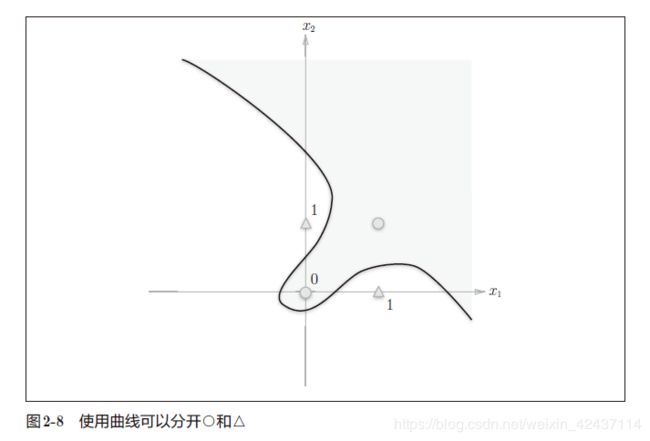
感知机的局限性

单层感知机无法分离非线性空间

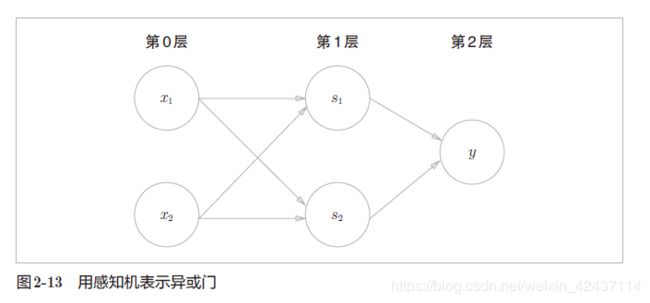
感知机通过叠加层实现异或门

感知机的绝妙之处在于它可以“叠加层”，组成多层感知机来分离非线性空间，进行非线性的表示。
多层感知机即是一种多层结构的神经网络。已有研究证明，2 层感知机（严格地说是激活函数使用了非线性的sigmoid 函数的感知机，可以表示任意函数。

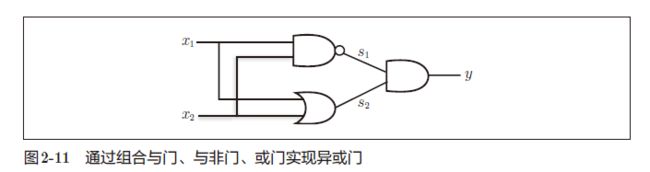
@test_gate(True)
def xor_gate(x1, x2):
    s1 = nand_gate(x1, x2)
    s2 = or_gate(x1, x2)
    return and_gate(s1, s2)

if __name__ == '__main__':
    xor_gate(0, 0)

代码输出：

xor_gate :
(0, 0) -> 0
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 0