列主元高斯消去法的实现，并且每一次的消去过程都要寻找全主元（C语言代码）

一、程序分析

首先要求用户输入方程组的个数n，然后再输入相应的方程组的系数，系数用一个二维数组保存，这个数组的大小为n * (n+1)，共n行，每行有n+1个元素，这是因为在输入系数矩阵的同时，也把常数列b输进去，因此，二维数组的每一行有n个系数和1个常数b。其实，二维数组存储的是方程组的增广矩阵。n维多元方程组如图所示：

二维数组输入完毕之后，程序开始高斯消元法的计算。首先调用search函数，找到绝对值最大的元素，返回到变量position中，position是我自己定义的结构体MAX_POSITION类型，此结构体有两个整形变量x和y，用于存放位置坐标中的横坐标和纵坐标。之后再判断是否需要调用行交换函数和列交换函数。前面这些属于正式高斯消元前的准备工作，因为我们需要找到全主元并调整到主对角线上，所以才会涉及到行交换和列交换。调整好之后，调用Gauss函数，进行消元。因为需要消元n次，所以上述步骤放在一个n重的循环中。最后，调整计算结果的位置，行交换对方程组的计算没有任何影响，但是列交换会改变解的位置。比如说第2列和第四列交换了，那么最终计算出来的x2和x4的结果也应该互换。

二、程序关键语句描述

下面代码是寻找绝对值最大的元素所在位置的函数。现在正对第k个方程进行消元，在消元之前，需要先把剩余方程中系数绝对值最大的元素移动到第k行的主对角线上。假设主对角线的元素就是最大的，如果其余的元素比主对角线的元素还要大，那么就记录下此元素的位置。当所有的系数都遍历了一遍之后，就能找到绝对值最大的元素所在的位置。

MAX_POSITION search(float matrix[][MAX_SIZE + 1], int k,int n) {
	int i, j;
	MAX_POSITION position;
	float max = fabs(matrix[k][k]);
	position.x = k;
	position.y = k;
	for (i = k + 1; i < n; i++)
		for (j = k; j < n; j++)
			if (fabs(matrix[i][j]) > max) {
				max = fabs(matrix[i][j]);
				position.x = i;
				position.y = j;
			}
	return position;
}

下面的代码是高斯消元结束之后，把结果往回代入计算的过程。matrix[k][n]是消元之后第k行常数项b的值。同时，它也是xn的解。整个回代过程用两层循环实现，外层循环指的是正在计算第k行，内层循环则是计算xk的具体实现。

//结果回代过程
	float temp;	//临时变量
	for (int k = n - 1; k >= 0; k--) {
		temp = matrix[k][n];	//临时变量temp赋值常数列b[i];
		for (int j = n - 1; j > k; j--) {
			temp = temp - matrix[k][j] * x[j];
		}
		x[k] = temp;
	}

下面代码是对计算结果的顺序进行调整，数组order记录着列交换的情况（从第0列开始计数），比如说order数组的内容为{3,0,5,1,4,2}，这说明此时的第零列为原先的第三列，此时的第一列为原先的第0列，此时的第二列为原先的第5列，以此列推。此时求解出的x0应为初始输入时的方程组的x3的解，x1应为原先方程组x0的解。因此，在输出结果之前，应该先对结果进行调整。

//对计算结果进行调整，因为之前进行列交换时，改变了计算结果的顺序。
	float order_x[MAX_SIZE];	//调整之后的结果
	for (int i = 0; i < n; i++)
		for(int j = 0;j < n;j++)
			if (i == order[j]) {
				order_x[i] = x[j];
				break;
			}

三、实验结果

选取一个比较特殊的方程组进行测试

把选主元的代码注释掉，验证选主元对方程组求解的影响

验证奇异方程的求解问题

验证选主元函数的正确性

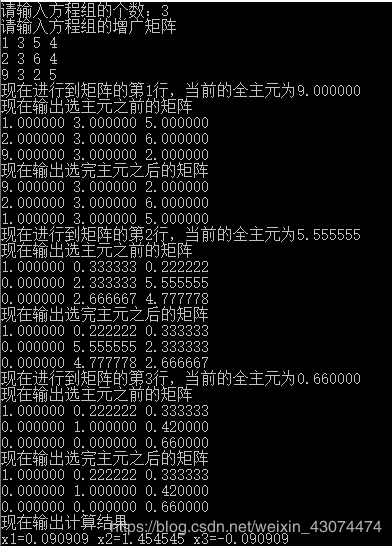
四、实验体会

当把选主元的代码给注释掉之后，同样的增广矩阵，程序却运算不出正确的结果了，这说明选主元在某些情形下是有必要的。比如说稀疏的增广矩阵，如果不进行选主元操作，很可能导致计算出非数或者带来较大的误差。但是选主元操作会给程序带来很大的压力，导致时间复杂度和空间复杂度增高，因此，实际应用时，应该根据方程组的实际情况，来确定是否选主元，是选列主元还是全主元。在验证奇异方程的求解问题时，发现出现了不可预知的结果。按照线性代数理论课上的知识，奇异方程的解是不唯一的，也就是说计算结果并不可靠，因此应尽量避免用高斯消去法求解奇异方程组。
最后，上源码，有问题欢迎给我留言。

#include "pch.h"	//非VS2017编译器请注释掉此行代码
#include
#include
#define MAX_SIZE 10
int order[MAX_SIZE];	//用order[i]标记此时的第i列是原先的第order[i]列
//主元素位置的结构体
struct MAX_POSITION {
	int x;
	int y;
};
//行交换函数
void raw_swap(float matrix[][MAX_SIZE + 1], int i, int j,int n){
	float temp[MAX_SIZE];
	int k;
	for (k = 0; k < n + 1; k++) {
		temp[k] = matrix[i][k];
		matrix[i][k] = matrix[j][k];
		matrix[j][k] = temp[k];
	}			
}
//列交换函数
void colum_swap(float matrix[][MAX_SIZE + 1], int i, int j, int n) {
	float temp[MAX_SIZE];
	int k = 0;
	for (k = 0; k < n; k++) {
		temp[k] = matrix[k][i];
		matrix[k][i] = matrix[k][j];
		matrix[k][j] = temp[k];
	}
	//标记第i列和第j列进行过交换
	float temp1;
	temp1 = order[i];
	order[i] = order[j];
	order[j] = temp1;
}
//从第k行开始，寻找绝对值最大的元素
MAX_POSITION search(float matrix[][MAX_SIZE + 1], int k,int n) {
	int i, j;
	MAX_POSITION position;
	float max = fabs(matrix[k][k]);
	position.x = k;
	position.y = k;
	for (i = k; i < n; i++)
		for (j = k; j < n; j++)
			if (fabs(matrix[i][j]) > max) {
				max = fabs(matrix[i][j]);
				position.x = i;
				position.y = j;
			}
	return position;
}
void Gauss(float matrix[][MAX_SIZE + 1], int k,int n) {		//对第k行运用高斯消去法
	int i,j;
	
	//第k行的每个系数都除以matrix[k][k]
	for (i = k + 1; i < n + 1; i++)
		matrix[k][i] = matrix[k][i] / matrix[k][k];
	//处理k+1行、k+1列之后的元素
	for(i = k + 1;i < n;i++)
		for (j = k + 1; j < n + 1; j++) {
			matrix[i][j] = matrix[i][j] - matrix[k][j] * matrix[i][k];
		}
	//主对角线元素变为1
	matrix[k][k] = 1;
	//第k列中，从k+1行开始，后面的元素都变为0
	for (i = k + 1; i < n; i++)
		matrix[i][k] = 0;
}
int main()
{
	float matrix[MAX_SIZE][MAX_SIZE + 1] = { 0 };
	int n;
	float x[MAX_SIZE] = { 0 };	//存放最终方程组的解
	MAX_POSITION position;
	printf("请输入方程组的个数：");
	scanf("%d", &n);
	printf("请输入方程组的增广矩阵\n");
	for(int i = 0;i < n;i++)
		for (int j = 0; j < n + 1; j++) {
			scanf("%f", &matrix[i][j]);
		}
	//初始化order[i]
	for (int i = 0; i < n; i++)
		order[i] = i;

	for (int k = 0; k < n; k++) {
		position = search(matrix, k, n);	//将绝对值最大的元素在数组中的位置存放到position中
		//观察选主元结果是否正确↓
		printf("现在进行到矩阵的第%d行，当前的全主元为%f\n", k + 1, matrix[position.x][position.y]);
		printf("现在输出选主元之前的矩阵\n");
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) 
				printf("%f ", matrix[i][j]);
			printf("\n");
		}
		//观察选主元结果是否正确↑
		if (k != position.x)	//主元素不在当前行
			raw_swap(matrix, k, position.x, n);
		if (k != position.y)	//主元素不在当前列
			colum_swap(matrix, k, position.y, n);
		//观察选主元结果是否正确↓
		printf("现在输出选完主元之后的矩阵\n");
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++)
				printf("%f ", matrix[i][j]);
			printf("\n");
		}
		//观察选主元结果是否正确↑
		Gauss(matrix, k, n);//进行高斯消元
	}

	//结果回代过程
	float temp;	//临时变量
	for (int k = n - 1; k >= 0; k--) {
		temp = matrix[k][n];	//临时变量temp赋值常数列b[i];
		for (int j = n - 1; j > k; j--) {
			temp = temp - matrix[k][j] * x[j];
		}
		x[k] = temp;
	}
	//对计算结果进行调整，因为之前进行列交换时，改变了计算结果的顺序。
	float order_x[MAX_SIZE];	//调整之后的结果
	for (int i = 0; i < n; i++)
		for(int j = 0;j < n;j++)
			if (i == order[j]) {
				order_x[i] = x[j];
				break;
			}
	//输出计算结果
	printf("现在输出计算结果\n");
	for (int i = 0; i < n; i++)
		printf("x%d=%f ", i + 1,order_x[i]);
}