从1开始学Java数据结构与算法——八种排序算法讲解分析与代码实现

算法的执行时间

要了解算法，就必须要了解算法的优劣之分，而算法的优劣之分很大一部分又取决于它的执行时间，那么在正式开始讲我们的八种算法之前，我们先讲解一下算法的执行时间这个问题

时间频度及其特点

时间频度：一个算法花费的时间与算法中语句的执行次数成正比，哪个算法中语句执行次数多，它花费的时间就多，一个算法中语句的执行次数称为时间频度，记为T(n)
举例说明：计算1到n的所有数字之和，我们有如下两种算法：

如果n=100的时候，左边的算法用了一个for循环，那么很显然语句要执行101次，所以时间频度T(n)=n+1。而右边的算法只有一条语句，只执行一次，时间频度T(n)=1。

知道了时间频度的概念之后，我们来看看它的特点：
1）下图中T(n)=2n+20与T(n)=2n两个时间频度，随着n的增大，他们的值会无限接近。同样的T(n)=3n+10与T(n)=3n两个时间频度也会随着n的增大而无限接近，那么这就得出了我们的第一个结论：时间频度中可以忽略常数项

2）下图中T(n)=2n²+3n+10与T(n)=2n²两个时间频度，随着n的增大，他们的值会无限接近。同样的T(n)=n²+5n+20与T(n)=n²两个时间频度也会随着n的增大而无限接近，那么这就得出了我们的第二个结论：时间频度中可以忽略低次项

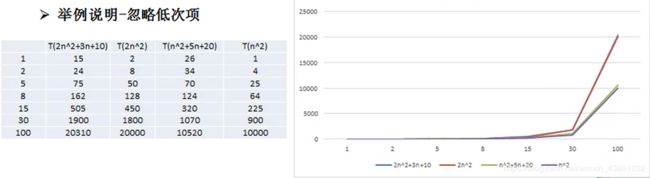
3）下图中T(n)=3n²+2n与T(n)=5n²+7n两个时间频度，随着n的增大，他们的值的差距会逐渐缩小，那么也就是说，当n无限大的时候，他们的值就会无限接近。再看另一组T(n)=n³+5n与T(n)=6n³+4n两个时间频度会随着n的增大两者的比值会无限接近6，那么这就得出了我们的剩余的两个结论：随着n的增大，3n²+2n与5n²+7n无限接近，可以忽略系数；随着n的增大，n³+5n与6n³+4n两条曲线分离，说明多少次方是关键

时间复杂度

判断一个算法执行时间的长短目前有两种方法：
  1）事后统计法：将一段程序运行起来后，再然后统计它运行的时间，那么这里有两个问题，一是我们需要实际运行这段程序，二是所得时间的统计量依赖于计算机硬件、软件等环境因素。那么这种方式需要在同一台计算机下才能比较哪个算法更快
  2）事前统计法：通过分析某个算法的时间复杂度来判断哪个算法更优

在了解了上面的时间频度之后，我们再来看一下时间复杂度：

• 一般情况下，算法中的基本操作语句的重复执行次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n接近无穷大时，T(n)/f(n)的极限值为不为零常数，则称f(n)是T(n)的同数量级函数，记作T(n)=O(f(n))，则称O(n)为算法的时间复杂度
• 举例说明：如果有个算法的时间频度为T(n) = n+1，有个辅助函数f(n) = n，那么T(n)/f(n)=1+1/n，就无限接近于一个不为零的常数，那么这个时候就可以说T(n)=O(f(n))=O(n)，而O(n)就是时间频度为T(N) = n+1该算法的时间复杂度
• 注意：不同的时间频度算法，是按复杂度可能相同，比如T(n)=n²+7n+6与T(n)=3n²+2n+2，时间复杂度都为n²
• 计算时间复杂度的方法：1.用常数1代替运行时间中所有加法常数；2.修改后的运行次数函数中，只保留最高阶项；3.去除最高阶项的系数 （这里为什么可以去除掉这些，就和我们上面分析的时间频度的特点有关了）
• 举例说明：比如T(n) = 3n²+2n+2，首先用1替换后得3n²+2n+1；接着只保留最高阶项得：3n²；接着去除最高阶项的系数得n²，所以时间复杂度即为O(n²)
• 常见得时间复杂度：（按执行快慢先后排序）
  
• 平均时间复杂度：指所有可能得输入实例均以等概率出现得情况下，该算法得运行时间
• 最坏时间复杂度：最坏情况下得时间复杂度

排序法	平均时间	最差情况	稳定度	额外空间	备注
冒泡	O(n²)	O(n²)	稳定	O(1)	n小时较好
交换	O(n²)	O(n²)	不稳定	O(1)	n小时较好
选择	O(n²)	O(n²)	不稳定	O(1)	n小时较好
插入	O(n²)	O(n²)	稳定	O(1)	大部分已排序时较好
基数	O(logRB)	O(logRB)	稳定	O(n)	B是真数(0-9)，R是基数(个十百)
希尔	O(nlogn)	O(n^s) 1	不稳定	O(1)	s是所选分组
快速	O(nlogn)	O(n²)	不稳定	O(nlogn)	n大时较好
归并	O(nlogn)	O(nlogn)	稳定	O(1)	n大时较好
堆	O(nlogn)	O(nlogn)	不稳定	O(1)	n大时较好

8种算法简介

上面介绍完了时间复杂度的概念之后，下面我们正式开始讲8大排序算法

排序也称排序算法，指将一组数据，依指定的顺序进行排列的过程

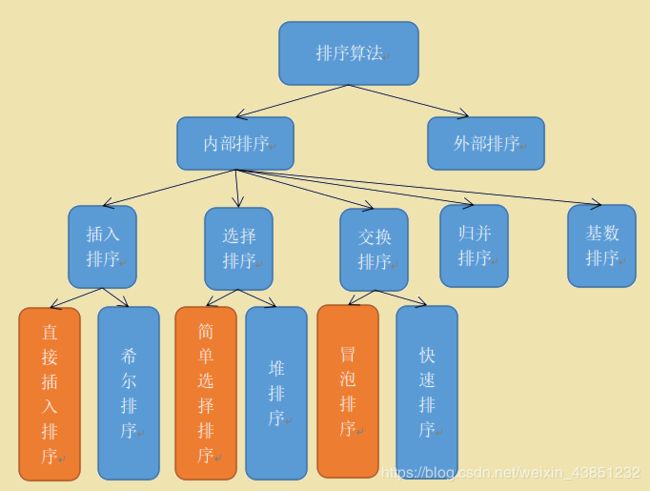
排序分类：内部排序和外部排序。内部排序：将需要处理的数据全部加载到内部存储器中进行排序。外部排序：如果数据量过大，比如有10亿条，无法全部加载进内存，那就需要借助外部存储器进行排序

其中内部排序又分为如下图几类，其中红色部分的直接插入排序，简单选择排序和冒泡排序是程序员作为最基础排序算法一定要掌握的，但随着目前市场对IT技术人员要求的不断提高，剩余的这些排序算法，也是很有必要掌握的

冒泡排序

思路分析

对一个给的那个的数组中的元素：3,-9,-1,10,20，我们对其进行从左至右的两两比较，如果相邻的两个数为逆序(也就是违背我们排序规则，从小到大，或者从大到小)，那么就将这两个元素位置进行交换，直到所有元素都按顺序排好。那么这离我们发现显然只通过一轮基本是不可能实现排序的，那么究竟需要多少轮呢？

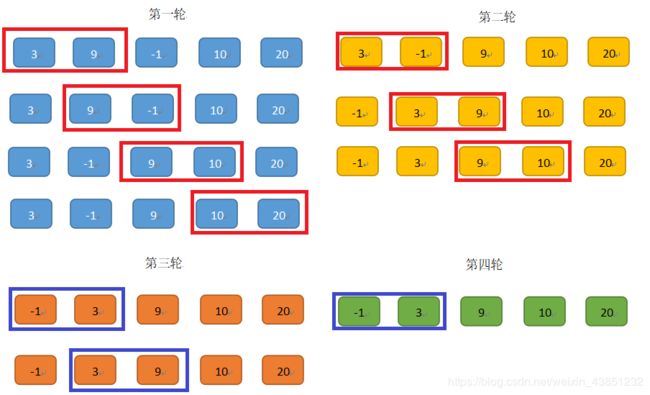
下面我们图解来看看：（从小到大排序）
图中的每一大轮都对数组中的每两个相邻元素进行比较，如果前面的比后面的小，就进行位置交换，那么每一大轮下来都能确定好最后一个位置的数是最大的。所以每一大轮两两比较的次数都比上一轮少一次
那么从下图能发现，数组里有5个元素，那么大轮就需要比较4轮，而一个大轮里小轮的比较次数会随着大轮轮数的增加而每次减一
那么假设我们有x个元素，那么大轮就需要进行x-1次，而每个大轮里面的小轮就需要进行x-1-i次（i是大轮的轮次数，比如第一轮就减1）

代码实现

/**
	 * 冒泡排序的具体方法(从小往大排)
	 * @param arr：传进一个需要被排序的数组
	 */
	public static void bubble(int[] arr) {
		int temp = 0;//用于交换的临时变量
		for(int i = 0; i<arr.length-1; i++){//外层循环用于排序排几轮
			for(int j = 0; j<arr.length-(1+i); j++) {//内层循环用于每一大轮中进行数据交换
				if(arr[j] > arr[j+1]) {
					//如果前面的数大于后面的，就进行交换
					temp = arr[j];
					arr[j] = arr[j+1];
					arr[j+1] = temp;
				}
			}
		}
	}

算法优化

从上面的思路分析中我们可以发现一个问题，其实在进行到第二大轮的第二小轮比较中，排序就已经成功了，而冒泡排序法还在继续完成后面没有意义的比较。那么我们就可以减少冒泡排序中后续不必要的比较，来对该算法进行优化。
我们可以设置一个boolean标志，用来判断是否进入了交换的代码片段中，如果在某一大轮两两比较都没有进入交换的话，那说明此时已经排序号，可以提前停止

选择排序

思路分析

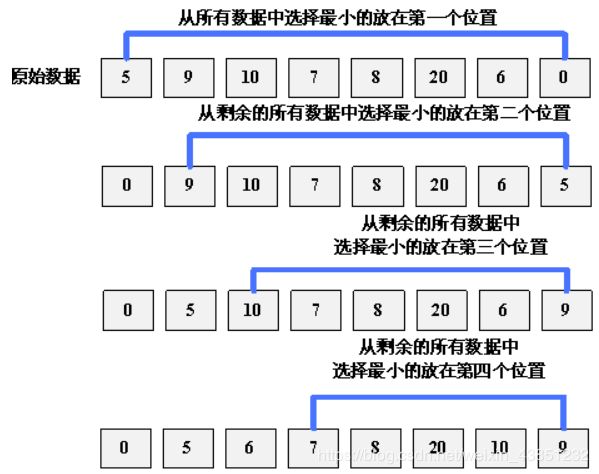
选择排序和冒泡排序其实有些相似，选择排序的核心思想是（从小到大排序）：第一次从arr[0]到arr[n]中找出最小的一个元素，将它与第arr[0]位置交换，第二次从arr[1]到arr[n]中找出最小的一个元素，将它与第arr[1]位置交换，第三次从arr[2]到arr[n]中找出最小的一个元素，将它与第arr[2]位置交换…依次进行下去，总共通过n-1次，排序完成

代码实现

public static void select(int[] arr) {
		int index = 0;//用来存放每一轮中找出的最小的数的下标位置,初始化从0开始
		for(int j=0; j<arr.length-1; j++) {//一共要找arr.length-1次
			//下面开始找每一轮中的最小值
			for(int i=j ; i<arr.length; i++) {//每一次都要循环数组
				if(arr[i] < arr[index]) {
					//如果有数比arr[index]小的话，重置一下index的位置
					index = i;
				}
			}
			//每一轮遍历完之后，都要进行位置的交换，将小的放到前面的位置
			int temp = arr[j];
			arr[j] = arr[index];
			arr[index] = temp;
			index = j+1;//最后重置index，使其位置后移一位
		}
	}

插入排序

思路分析

对于给定的一组数据，我们讲其分为两部分，一部分为有序表，一部分为无序表，我们规定一开始有序表只有一个该组数据中最左边的一个元素，然后从该组剩余数据中从左往右，每次取一个数据，与有序表中的元素进行比较，找到合适的插入位置插入，直到全部元素都放入有序表中即完成。下面给出图解：
这里我们以101，34，119，1这组数据为例子，拿到该组数据之后，按照上诉思路分析，先将数据分为有序和无序两部分

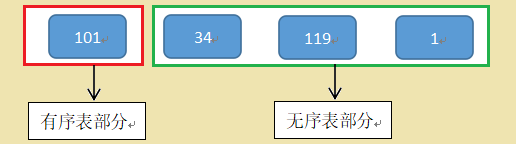
接着从无序部分开始，从左往右依次取一个数，与有序部分中的元素进行大小比较，然后插入到合适的位置中



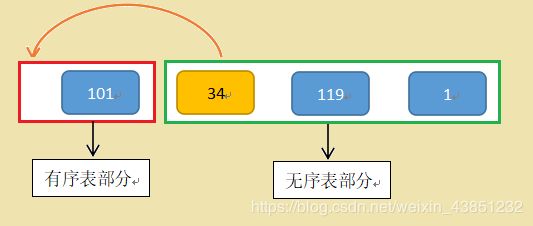
最终排好序得到的结果如下图

代码实现

/**
	 * 插入排序法，这里以从小到大排列
	 * @param arr:传入的数据数组
	 */
	public static void insertsort(int[] arr) {
		int temp = 0;//这里需要一个变量去存放当前需要被排序的元素
		int index = 0;//这个j是用来对被插入元素进行位置的扫描的索引
		//从该组数据的第二个数据开始排序，第一个数据默认在有序部分里，并一开始以它为标准进行大小比较
		for(int i = 1; i<arr.length; i++) {
			temp = arr[i];//存放当前需要被排序的元素，因为后面我们是通过后移位置的方式来空出需要被插入的位置
			index = i;//从有序部分的最右边的一个数开始扫描，进行大小比较，确定插入位置
			//开始寻找插入位置
			while(index >= 1 && temp < arr[index-1]) {
				//位置后移
				//这里的arr[i]为当前需要被排序的元素，它被覆盖掉了没关系的，因为我们前面已经用temp存放了
				arr[index] = arr[index-1];
				index--;
			}
			//找到插入位置，将temp中存放的需要被排序的数据，插入到该位置中
			arr[index] = temp;
		}
	}

这里我们是从小到大排序，那如果要变成从大到小排序怎么办呢，很简单，只要将while里的temp < arr[index-1]这个条件改为temp < arr[index-1]即可

存在的问题

从上面的过程中我们可以看到，我们的插入是通过后移元素位置进行的，如下图

那么我们就会发现，当从小到大排列，且数据给的是23451的时候有，只需要将1插入到最前面，就需要进行很多次的移动，那如果数据中有234567891，或者更多的时候，这个效率显然是非常低的，那么下面我们来看看希尔排序

希尔排序

希尔排序也是一种插入排序，是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序

思路分析

给到一组n个需要排序的数据，我们对其进行分组，第一次以n/2为步长，分为n/2个组，后续每次都再除以2进行分组。每次分完之后，在组内进行排序，直到分到最后一次，每组的元素为一个的时候，再进行一次总的排序，即完成希尔排序

以8917235460这组10个数据进行图解（从小到大）：
1）先10/2=5，所以我们先将其以5为步长分为5组：

2)将上诉分组之后，在组内进行排序，也就是8和3，9和5，1和4，7和6，2和0两两进行插入排序，排好后如下图

3)再进行除以2，也就是5/2=2.5，这里取整，取2，所以得到如下分组：

4)再在组内进行插入排序，31097为一组进行排序，56842为一组进行插入排序，结果如下：

5)最后在进行分组的时候，发现2/2=1，那么也就是到最后一轮了，直接对全部进行排序即可，最终结果如下图

其实在我们进行希尔排序的时候，我们可以采用交换法（速度相对较慢）和位移法（速度相对较快），那么下面再希尔排序的代码实现中，我们两种方法都会实现一下

代码实现

交换法

/**
	 * 希尔排序的交换法实现
	 * @param arr:传入的数据数组
	 */
	public static void shellsort_swap(int[] arr) {
		int temp = 0;//用于交换的临时变量
		//分组,从第一次/2开始
		for(int group = arr.length/2; group>=1; group=group/2) {
			//组间的循环
			for(int j = group; j<arr.length; j++) {
				//每组组内的元素操作,从第一个元素开始
				for(int i = j-group; i >= 0; i=i-group) {
					//组内排序，只要发现两个相邻的大小顺序不对，就交换
					if(arr[i] > arr[i+group]) {
						temp = arr[i];
						arr[i] = arr[i+group];
						arr[i+group] = temp;
					}
				}
			}
		}
	}

位移法

/**
	 * 希尔排序的位移法实现
	 * @param arr:传入的数据数组
	 */
	public static void shellsort_displacement(int[] arr) {
		int temp = 0;//用来存放需要被排序的元素
		//分组,从第一次/2开始
		for(int group = arr.length/2; group>=1; group/=2) {
			//组间的循环
			for(int i = group; i<arr.length; i++) {
				//每组组内的元素操作,从第一个元素开始
				int j = i;
				temp = arr[j];//存放需要被排序的元素
				//组内排序，位移法
				while(j-group>=0 && temp < arr[j-group]) {
					arr[j] = arr[j-group];//位置取代
					j = j-group;//位置移动
				}
				//找到插入的位置
				arr[j] = temp;
			}
		}
	}

快速排序

思路分析

快速排序是对冒泡排序的一种改进。基本思想是：
一组数据中，以一个数为基准，分成左右两部分，左边的数都比这个基准数小，右边的都比这个基准数大，然后再在左右两部分中，按照上述方法，继续分，直到排序完成为止。
如下图，先以0为基准分为左右两部分，左边只有两个数，随便取哪个数当基准，这里都相当于是一个位置交换的问题，结果都一样，直接能排好这两数的顺序。而在右边的三个数里，再以70为基准，继续排序。

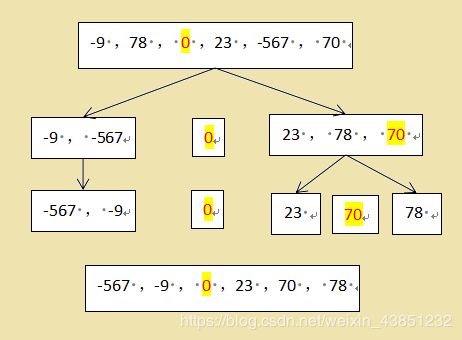
那么这里通过分析我们可以看到，左右两部分的分割排序其实是一个重复的过程，那么我们就可以用到递归的方法
下面的代码，里面还考虑了奇偶个数的情况，里面可能有些地方再思路分析中没有写到，大家看着注释，自己手动画画图慢慢理解一下吧

代码实现

/**
	 * 快速排序
	 * @param
	 * 		arr:需要被排序的数组
	 * 		left:左端开始扫描位置
	 * 		right:右端结束扫描位置
	 */
	public static void quicksort(int[] arr,int left, int right) {
		int l =left;//左下标，作为左边的索引
		int r = right;//右下标，作为右边的索引
		int pivot = arr[(left+right)/2];//基准数
		int temp = 0;//用于交换的临时变量
		//如果左边一直没有大于等于右边的话，说明左右两边还没扫描完毕
		//这里说明一下，当数据为奇数个的时候，左右两边扫描完毕后，l=r，为偶数个的时候，l>r
		while(l<r) {
			//如果在左边发现有数大于基准数,但是这里注意，我们有可能遇到arr[l] == pivot的情况
			while(arr[l] < pivot) {
				l += 1;//那么当这个while退出的时候，l就是需要被更改位置的左边的下标
			}
			//如果在右边发现有数小于基准数,但是这里注意，我们有可能遇到arr[r] == pivot的情况
			while(arr[r] > pivot) {
				r -= 1;//那么当这个while退出的时候，l就是需要被更改位置的右边的下标
			}
			//如果上面两个while是当arr[l] = pivot和arr[r] = pivot才退出的，那么此时l=r
			//也就说明，pivot左边已经都是小于它的数，pivot右边已经都是大于它的数
			if(l >= r) {//这里写的l>=r，其实l理论来说是不可能大于r的，所以这里只有=在生效
				break;
			}
			//否则的话，就将左边大于pivot的数，和右边小于pivot的数进行位置交换就可以了
			//这里交换的时候注意，上面说了，可能遇到arr[r] == pivot或者arr[l] == pivot也被交换了的情况
			temp = arr[l];
			arr[l] = arr[r];
			arr[r] = temp;
			//因为交换完了之后，算法还在whie(l
			//所以还会继续判断while(arr[l] < pivot)和while(arr[r] > pivot)
			//那么如果是arr[r] == pivot或者arr[l] == pivot的情况的话，因为l和r无法移动，就会现如交换的死循环
			//所以接下来我们处理arr[r] == pivot或者arr[l] == pivot的这种情况
			//如果arr[l] == pivot,注意这里的arr[l]已经被交换到了右边，所以这r--，直接跳过这个数,否则会陷入死循环
			if(arr[l] == pivot) {
				r--;
			}
			//如果arr[r] == pivot,注意这里的arr[r]已经被交换到了左边，所以l++，直接跳过这个数,否则会陷入死循环
			if(arr[r] == pivot) {
				l--;
			}
		}
		//对于奇数个的元素，因为在上面的扫描中，如果某一轮左右两边的数据都不需要交换
		//那么l和r就会一直扫描，直到相等且=pivot的位置(也就是正中间的位置),但是对于偶数个的元素就没有这个问题
		//退出大while(l
		if(l == r) {
			l += 1;
			r -= 1;
		}
		//向左递归
		if(left < l) {
			//这里的left始终是0
			//而r(也就是右端)是上一轮的右边部分到达中间值后再-1,变为下一轮的左边部分的最右端
			quicksort(arr, left, r);
		}
		//向右递归
		if(right > r) {
			//这里的right始终是arr.length-1
			//而l(也就是左端)是上一轮的左边部分到达中间值后再+1,变为下一轮右边部分的最左端
			quicksort(arr, l, right);
		}
	}

归并排序

归并排序是利用归并的思想进行排序方法，该算法采用经典的分治策略（分治法将问题分解为一些小的问题然后递归求解，而治的阶段则将得到的各答案修补在一起，即分而治之），这里可以先有个分治的概念，后面的博客我们还会讲到分治算法

思路分析

归并排序主要分为两部分，分和治。
这里的分有点像快速排序，但是快速排序中是找一个基准数进行大小的比较，然后分为左右两部分，但是归并排序中，只是单纯的讲一个数组分为左右两部分。并不考录左右两部分的大小比较，只是单纯的讲该数组分解为几个更小的部分
所谓分：就是讲该数据每次折半分为两部分，然后依次递归分解下去，直到最后分为一个一个的，不能再分为止
所谓治：就是将分出来的再按顺序合并到一起，最终使得整体数据有序。

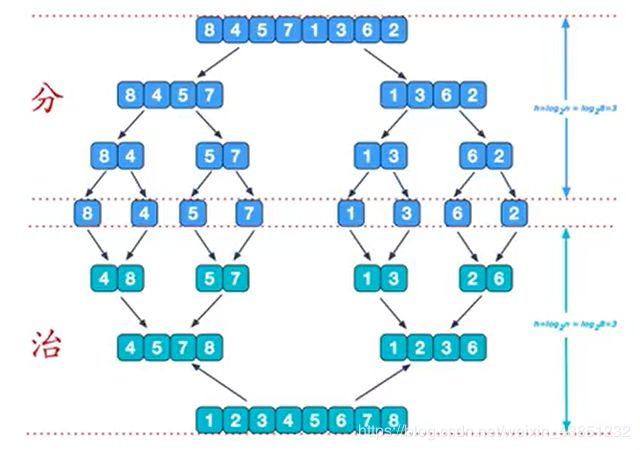
那么在分的过程中，我们可以采用递归的方式去分解，然后在递归分解完成开始回溯的时候，进行合并的操作
其实分解的过程并不难，这里比较重要的是如何进行治，也就是如何进行排序合并的过程。下面我就用上图的4578和1236这两部分的合并进行一个图解:
这里我们要知道一个前提：左右两边均已是从小到大排序好的
1）首先我们需要一个额外的数组去做一个临时存放，然后依次给左边部分一个初始索引，右边部分一个索引，还需要给额外的临时数组一个索引，用于确定放入的位置

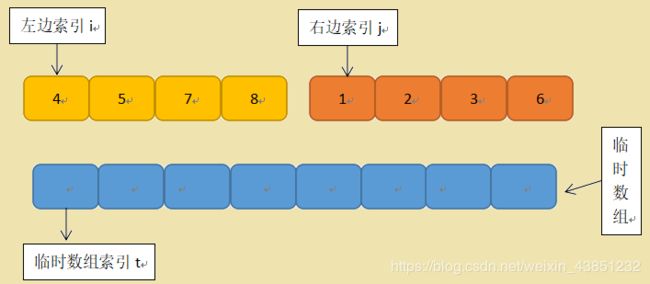
2)左边索引指向的值与右边索引指向的值进行大小比较，将较小一边的数据放入临时数组索引指向的位置，然后将较小一边的索引和临时数组的索引都后移一位，那么这里就是右边的值1比较小，将它放入t所指的位置，然后j后移一位，t也后移一位

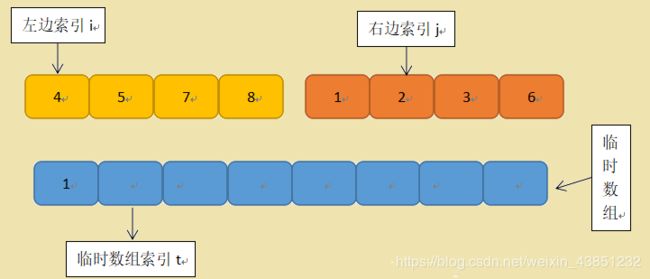
3）重复2）过程，继续比较，直到又一边的数据先全部放完。

4）将剩余一边的数据按顺序放入临时数组的位置即可

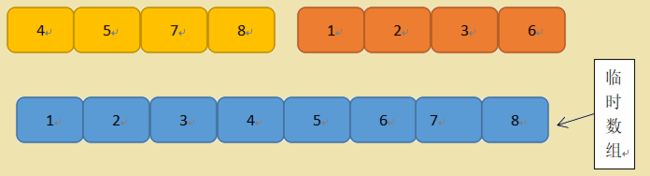
5)将临时数组中的数据，按顺序拷贝回原来的数组中

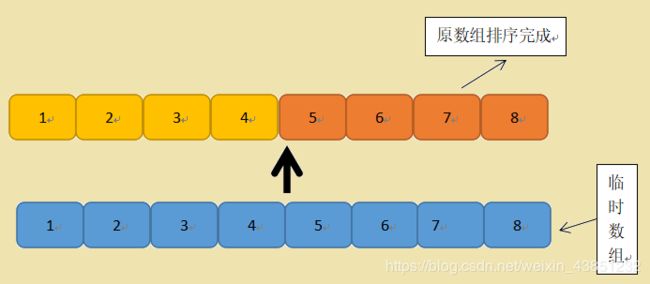
代码实现

	/**
	 * 递归分解，回溯的时候合并
	 * 		arr[]:需要被排序的数组，原始数组
	 * 		left:每部分的最左边
	 * 		right:每部分的最右边
	 * 		temp:临时数组
	 */
	public static void mergersort(int[] arr, int left, int right, int[] temp) {
		if(left<right) {
			int middle = (left+right)/2;//中间索引
			//向左递归分解
			mergersort(arr, left, middle, temp);
			//向右递归分解
			mergersort(arr, middle+1, right, temp);
			//回溯合并
			merge(arr, left, right, middle, temp);
		}
	}
	
	/**
	 * 合并方法
	 * @param
	 * 		arr[]:需要被排序的数组，原始数组
	 * 		left:每部分的最左边
	 * 		right:每部分的最右边
	 * 		middle:中间索引
	 * 		temp:临时数组
	 */
	public static void merge(int arr[], int left, int right, int middle, int[] temp) {
		int i = left;//初始化i，使其指向左边部分的第一个位置
		int t = 0;//临时数组的索引，初始化在第一个位置
		int j = middle+1;//初始化j，使其指向需要被分割到右边的第一个位置
		
		//1.比较左右两部分的大小，依次放入临时数组中
		while(i<=middle && j<=right) {
			//如果左右两部分索引都还没扫描完，就一直进行比较放入的过程
			if(arr[i] <= arr[j]) {
				//左边部分放入临时数组中
				temp[t] = arr[i]; 
				//索引后移
				t++;
				i++;
			}else {
				//右边部分放入临时数组中
				temp[t] = arr[j]; 
				//索引后移
				t++;
				j++;
			}
		}
		//上面一个while出来后，说明左右两边有一边已经全部放完，那么就要对剩余的一边进行放入操作
		//2.将左右两边剩余一遍的剩余一部分按顺序放入临时数组的剩余位置中
		while(i<=middle) {
			temp[t] = arr[i]; 
			//索引后移
			t++;
			i++;
		}
		while(j<=right) {
			temp[t] = arr[j]; 
			//索引后移
			t++;
			j++;
		}
		
		//上面两个while只会执行其中一个，执行完后，临时数组中已经按顺序放好数据
		//3.将临时数组中的数据按顺序拷贝到原数组中
		//但是这里注意我们不是每一次都将临时数组中的所有数据拷贝到原数组中
		//因为并不是每一次临时数组中都会装满数据！！！,而且每次拷回原数组中，也不是都从原数组中的第一个位置开始放的
		//比如8,4,5,7,1,3,6,2最后会分单个数据之后的第一轮合并，是合并8、4；5、7；1、3；6、2
		//那么按顺序合并后的48放入原数组的0和1的位置，但是57要放入原数组2和3的位置，这里就是一个小细节处理
		
		t = 0;//这里先让临时数组的索引回到最初的位置先，从第一个数据开始拷贝
		int templeft = left;//为了解决上面的位置问题，这里用一个变量取存放left，而left就是每次要放入位置的开始
		while(templeft <= right) {
			arr[templeft] = temp[t];
			templeft++;
			t++;
		}
		
	}

基数排序

基数排序属于“分配式排序”，又称桶子法或bin sort，顾名思义它是通过键值的各个位的值，将要排序的元素分配至某个桶中，以达到排序的目的

思路分析

先将所有待比较的数值统一为同样长度的位数，数位较短的前面补零，然后从最低位开始，依次进行依次排序。这样从最低位一直到最高位排序完成以后，数列就变成一个有序数列。下面以53，5，542，748，14，24为例子给个图解：
1）先将他们补成同样长度的位数053，005，542，748，014，024，然后先比较个位，依次放入对应的桶中

2)将个位数比较完后得到的结果，拿到后，再进行十位数的比较，依次放入对应的桶中

3)将十位数比较完后得到的结果，拿到后，再进行百位数的比较，依次放入对应的桶中，那么因为数据中的最高位数就为百位，所以改论排序过后即得到最终结果

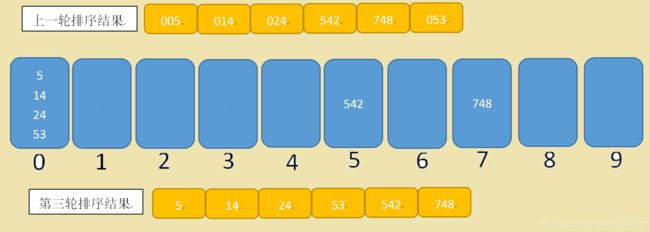
代码实现

/**
	 * 基数排序
	 */
	public static void radixsort(int[] arr) {
		
		//定义一个二维数组，用于表示桶,这里一共有10个桶，为了放置溢出，每个桶需要arr.length个位置
		//这里我们就发现了，其实基数算法每个桶需要arr.length个位置是很浪费空间的，所以这是一个经典的以空间换时间的算法
		int bucket[][] = new int[10][arr.length];
		//定义一个一维数组，用来确定每个桶中的存放了数据的个数
		int[] bucketElementCount = new int[10];
		
		//先要确定最大的数共有几位，才能确定我们要比较的轮数
		int time = arr[0];//确定最大位数，以确定比较的轮数
		for(int i = 1; i<arr.length-1; i++) {
			if(time < arr[i]) {
				time = arr[i];
			}
		}
		time = (time+"").length();//这里的time已经确定好了要循环比较的轮数
		for(int i = 0; i<time; i++) {
			//开始每一轮的循环
			for(int j = 0; j<arr.length; j++) {
				//循环每个数，按照轮数取其对应的位数（第一轮取个位，第二轮取十位...）
				int digit = (int) (arr[j] / Math.pow(10, i) % 10);//取对应的位数
				//根据取出的位数将该数放入对应的桶中
				//bucket[][],第一个位置表示放入第几个桶(也就是对应位数是多少)，第二个填放入该桶的第几个位置
				//bucketElementCount[digit]表示第digit个桶里有多少个数据
				bucket[digit][bucketElementCount[digit]] = arr[j];
				bucketElementCount[digit]++;
			}
			int index = 0;//这里需要一个变量，来确定从桶中取出的数据，放入原数组的第几个位置
			//全部数据放完之后，遍历每个桶，将它们里面的数据按顺序取出
			for(int k = 0; k<bucket.length; k++) {
				//如果桶中有数据，就按顺序取出
				if(bucketElementCount[k] != 0) {
					//循环该桶取出数据
					for(int n = 0; n<bucketElementCount[k]; n++) {
						arr[index] = bucket[k][n];
						index++;
					}
					//这里注意，每一次该桶取完数据之后，记得要将第k个桶归零！！！bucketElementCount[k]
					//让下一轮可以从每个桶的第一个位置开始放，否则就会导致位置错乱，取出的是错误数据
					bucketElementCount[k] = 0;
				}
			}
		}
	}

基数排序的空间问题

上面的代码我们可以看到，在进行基数排序的过程中，我们需要额外的一个二维数组取表示桶，还需要一个额外的以未数组取记录每个桶中数据的个数。其实基数排序是一个经典的用空间换时间的算法，下面我们就来测试一下它的空间和时间：
我们随机生成800万个[0,8000000)的随机数，然后对其进行基数排序，先来看看要耗时多久

//我们用随机生成800w个数据，来进行排序
		int arr[] = new int[8000000];
		for(int i = 0; i < 8000000; i++) {
			arr[i] = (int)(Math.random()*8000000);//随机生成一个[0，800000)的数
		}
		
		Date time_one = new Date();
		SimpleDateFormat simpleDateFormat_one = new SimpleDateFormat("yyyy-MM-dd:HH:mm:ss");
		String date_one = simpleDateFormat_one.format(time_one);
		System.out.println("排序前的时间:"+date_one);
		
		radixsort(arr);//基数排序
		
		Date time_two = new Date();
		SimpleDateFormat simpleDateFormat_two = new SimpleDateFormat("yyyy-MM-dd:HH:mm:ss");
		String date_two = simpleDateFormat_two.format(time_two);
		System.out.println("排序后的时间:"+date_two);

运行结果如下图：我们发现排八百万个数据，基数排序只需要3秒左右，还是非常快的，那如果我们把数据加到八千万个呢？会发生什么事情呢？

这里我们先不急着跑代码，我们先来算一下：一共有80000000个int数据，一个int数据有4个字节，且因为我们需要十个和数组相同大小的桶，所以我们需要的额外空间10×80000000×4 / 1024 / 1024 / 1024
10×80000000×4 / 1024 / 1024 / 1024 ≈2.9G这已经是个非常可怕的内存消耗了，我们排序拍八千万个数据就需要2.9个额外的空间消耗，对于有些机器在运行的过程中可能就会报内存不足$OutOfMemoryError$的错误，而导致排不了序

堆排序

这个排序由于我们现在还没到二叉树的内容模块，所以堆排序的内容我放到了从1开始学Java数据结构与算法——树结构的实际应用（一）：堆排序、赫夫曼树、赫夫曼编码.这篇博客里

写在最后

上面我已经写了一种方法去测试排序的速度，就是随机生成大量的数据，并打印排序前后的时间来测试，根据这个方法，我把之前七种方法排序的大概的时间写在下面，但是这个时间会根据电脑的配置不同而不同，所以仅供参考

方法	时间
冒泡排序	8w个数据，耗时12s左右
选择排序	8w个数据，耗时2s左右
插入排序	8w个数据，耗时2s左右
希尔排序	800w个数据，耗时3s左右
快速排序	80w个数据，耗时1s左右
归并排序	800w个数据，1s左右
基数排序	800w个数据，3s左右

下一篇: 从1开始学Java数据结构与算法——四种查找算法讲解分析与代码实现.