点击查看:蓝桥杯历年真题 题解目录
剪邮票
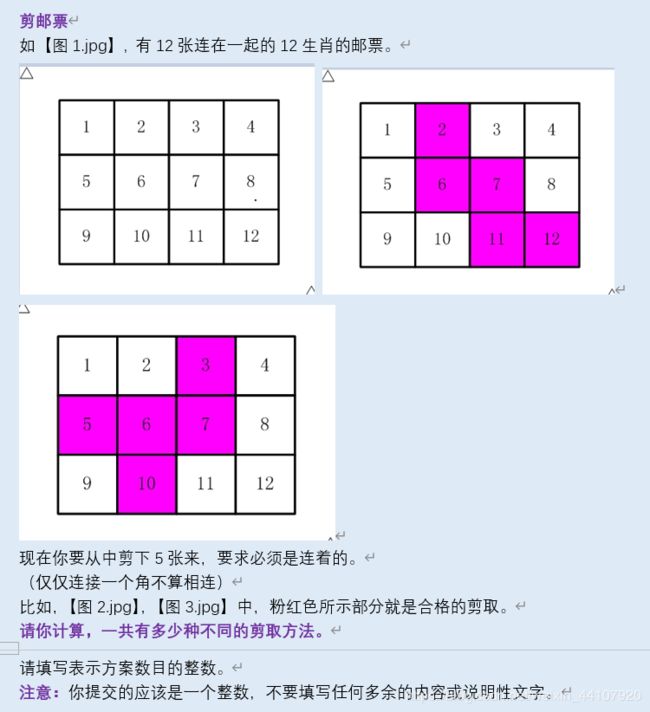
答案: 116
思路分析:
1. 因为dfs只能一条道走到黑,不能产生"T"字型的邮票
2. 即在12个方格中选出5个方格,判断是否能连成一块,即判断连通块的个数
如果有1个连通块 说明5张邮票相邻,ans++;
3. 对 a[] = {0,0,0,0,0,0,0,1,1,1,1,1};进行全排列,用Set集合去重,以保证不重复计数
4. 全排列的模板很简单,代码中已注释
5. 将一维数组a 转为二维数组 t ,数组中的每个元素代表该邮票是否被选中(1为选中,0未选中)
6. 然后转化为求解连通块的问题及模板
7. if(连通块的个数==1) ans++;
8. 因为涉及到 12个元素的全排列,程序运行耗时约 1 min,但这是结果填空题,so问题不大
package java_B_2016;
import java.util.Set;
import java.util.TreeSet;
public class Main007_剪邮票 {
static int size;
static int a[] = {0,0,0,0,0,0,0,1,1,1,1,1};
static int t[][] = new int[3][4];
static int ans;
static Set<String> set = new TreeSet<String>();
public static void main(String[] args) {
f(0);
System.out.println(ans);
}
private static void f(int k) {
if(k==12) {
StringBuffer sb = new StringBuffer();
for(int i=0;i<12;i++) {
sb.append(a[i]);
}
set.add(sb.toString());
if(set.size()>size) {
size=set.size();
for(int i=0;i<3;i++){
for(int j=0;j<4;j++) {
t[i][j]=a[4*i+j];
}
}
int count=0;
for(int i=0;i<3;i++)
for(int j=0;j<4;j++)
if(t[i][j]==1) {
dfs(i,j);
count++;
}
if(count==1) ans++;
}
}else {
for(int i=k;i<12;i++) {
int t = a[i]; a[i] = a[k]; a[k] = t;
f(k+1);
t = a[i]; a[i] = a[k]; a[k] = t;
}
}
}
private static void dfs(int i, int j) {
t[i][j]=0;
if(i+1<=2&&t[i+1][j]==1) dfs(i+1, j);
if(i-1>=0&&t[i-1][j]==1) dfs(i-1, j);
if(j+1<=3&&t[i][j+1]==1) dfs(i, j+1);
if(j-1>=0&&t[i][j-1]==1) dfs(i, j-1);
}
}

下面这个方法可以秒出结果
public class Main007_剪邮票2 {
static int a[] = {0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1};
static int ans;
static void dfs(int g[][], int i, int j) {
g[i][j] = 0;
if (i - 1 >= 0 && g[i - 1][j] == 1) dfs(g, i - 1, j);
if (i + 1 <= 2 && g[i + 1][j] == 1) dfs(g, i + 1, j);
if (j - 1 >= 0 && g[i][j - 1] == 1) dfs(g, i, j - 1);
if (j + 1 <= 3 && g[i][j + 1] == 1) dfs(g, i, j + 1);
}
static boolean check(int path[]) {
int g[][]=new int[3][4];
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 4; ++j) {
if (path[i * 4 + j] == 1) g[i][j] = 1;
else g[i][j] = 0;
}
}
int cnt = 0;
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 4; ++j) {
if (g[i][j] == 1) {
dfs(g, i, j);
cnt++;
}
}
}
return cnt == 1;
}
static boolean vis[]=new boolean[12];
static void f(int k, int path[]) {
if (k == 12) {
if (check(path)) {
ans++;
}
}
for (int i = 0; i < 12; ++i) {
if (i > 0 && a[i] == a[i - 1] && !vis[i - 1])
continue;
if (!vis[i]) {
vis[i] = true;
path[k] = a[i];
f(k + 1, path);
vis[i] = false;
}
}
}
public static void main(String[] args) {
int path[]=new int[12];
f(0,path);
System.out.println(ans);
}
}

