使用以下商品房销售记录表数据，用梯度下降法，编程实现一个房价预测系统

题目描述

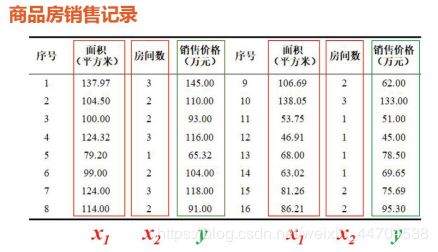
使用以下商品房销售记录表数据，用梯度下降法，编程实现一个房价预测系统。

求解原理

给定的数据集dataSet，每一行代表一组数据记录，每组数据记录中，第一个值为房屋面积（单位：平方米），第二个值为房间数，第三个值为销售价格（单位：万元）。利用梯度下降法，构建损失函数，在函数gradientDescent中实现销售价格price和房屋面积area和房间数rooms的线性回归，返回值为线性方程：

中系数

的列表。
损失函数：估量模型的预测值与真实值的不一样程度。这里选用均方差为损失函数，如下：

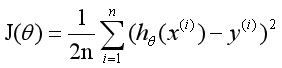
n：是数据集中的个数
1/2：是一个常量，这样是为了在求梯度的时候，二次方乘下来就和这里的1/2抵消了，就没有多余的常数系数，方便后续的计算，同时对结果不会有影响
y：是数据集中每个点的真实y坐标的值
h：是我们的预测函数，根据每一个输入x，根据θ计算得到预测的y值
这里的
函数为

算法原理

梯度下降法：利用负梯度方向来决定每次迭代的新的搜索方向，使得每次迭代能使待优化的目标函数逐步减小。梯度是微积分中一个很重要的概念，在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率；在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向。
从损失函数

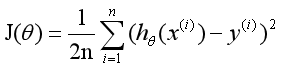
中可知，其中变量有三个

所以是一个多变量的梯度下降问题，求解出损失函数的梯度，也就是分别对三个变量进行微分：




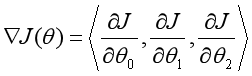
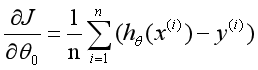
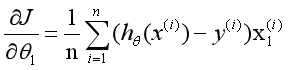
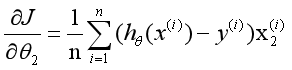
这个表达式的意思就是求θ的偏导，就是先将预测值
减去实际的值

的差乘以偏移量

的总和加起来除以所有的组数。
明确了代价函数和梯度，以及预测的函数形式。就可以开始编写代码了。
每次迭代时，都会有

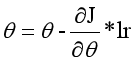
lr即learning rate，经过num_iterations次迭代后，最终梯度下降到最优解附近。此时，模型就训练成功。

编程求解

实现线性回归主要有三步：
第一步，获得训练的数据，也就是房子的大小，房间数以及销售价格。
第二步，设置初始的三个未知数
的值，也就是线性方程的系数，刚开始，随机为1，2，1。
第三步，根据设置的
的值，将相应的房间大小和房价数都放入函数中，求得一个预测的房价predict_y。用预测的房价减去实际的房价，对他们的结果求平方，并将这n组数据求得的平方结果累加起来。来计算一下损失函数（就是求均方差）。
每次预测完房子的价格，都将相应的
向真实的房价偏移，偏移量是(预测房价-真实房价)*相应的参数（如果是
，那就是乘以1，如果是
，那就是乘以area对应的值，如果是
，那就是乘以rooms对应的值），该偏移量是向上偏移（即函数中的系数值变大）还是向下偏移，取决于预测值predict_y是低于还是高于真实价格。
就这样一直进行偏移量操作，一直对
进行迭代。

import matplotlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from numpy import genfromtxt

# 采集数据样本
x1_area = np.array([137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00,114.00, 106.69, 138.05, 53.75, 46.91, 68.00, 63.02])
x2_rooms = np.array([3, 2, 2, 3, 1, 2, 3, 2, 2, 3, 1, 1, 1, 1])
y_price = np.array([145.00, 110.00, 93.00, 116.00, 65.32, 104.00, 118.00,91.00, 62.00, 133.00, 51.00, 45.00, 78.50, 69.65])
dataSet = np.zeros((len(x1_area), 3))
for i in range(len(x1_area)):
    dataSet[i, 0] = x1_area[i]
    dataSet[i, 1] = x2_rooms[i]
    dataSet[i, 2] = y_price[i]

"""
函数说明：对数据进行归一化
Parameters:
    dataSet - 特征矩阵
Returns:
    normDataSet - 归一化后的特征矩阵
    ranges - 数据范围
    minVals - 数据最小值
"""
def autoNorm(dataSet):
    # 获得数据的最小值,min(0)返回该矩阵中每一列的最小值
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    # 最大值和最小值的范围
    ranges = maxVals - minVals
    # shape(dataSet)返回dataSet的矩阵行列数
    normDataSet = np.zeros(np.shape(dataSet))
    # 返回dataSet的行数
    m = dataSet.shape[0]
    # 原始值减去最小值
    normDataSet = dataSet - np.tile(minVals, (m, 1))
    # 除以最大和最小值的差，得到归一化数据
    normDataSet = normDataSet / np.tile(ranges, (m, 1))
    # 返回归一化数据的结果，数据范围，最小值
    return normDataSet, ranges, minVals

normDataSet, ranges, minVals = autoNorm(dataSet)
# x = normDataSet[:, 0]
# y = normDataSet[:, 1]
# z = normDataSet[:, 2]
# # 绘制散点图
# fig = plt.figure()
# ax = Axes3D(fig)
# ax.scatter(x, y, z)
#
# # 添加坐标轴(顺序是Z, Y, X)
# ax.set_zlabel('Z', fontdict={'size': 15, 'color': 'red'})
# ax.set_ylabel('Y', fontdict={'size': 15, 'color': 'red'})
# ax.set_xlabel('X', fontdict={'size': 15, 'color': 'red'})
# plt.show()

# 计算误差
print(normDataSet)

def mse(theta, data):
    totalError = 0
    for i in range(0, len(data)):
        x1 = data[i, 0]
        x2 = data[i, 1]
        y = data[i, 2]
        totalError += (y - (theta[0] + theta[1] * x1 +theta[2] * x2)) ** 2
    return totalError/float(len(data))/2

#计算梯度
def step_gradient(theta_current, data, lr):
    theta0, theta1, theta2= 0, 0, 0
    area = data[:, 0]
    rooms = data[:, 1]
    price = data[:, 2]
    M = 14
    for i in range(0, len(data)):
        predict_y = theta_current[0] + theta_current[1] * area[i] + theta_current[2] * rooms[i]
        theta0 = (theta0 + (predict_y - price[i]) * 1) / M
        theta1 = (theta1 + (predict_y - price[i]) * area[i]) / M
        theta2 = (theta2 + (predict_y - price[i]) * rooms[i]) / M
    theta_current[0] = theta_current[0] - lr * theta0
    theta_current[1] = theta_current[1] - lr * theta1
    theta_current[2] = theta_current[2] - lr * theta2
    return theta_current

# 更新梯度
def gradient_descent(data, theta_star, lr, num_iterations):
    theta = theta_star
    for step in range(num_iterations):
        theta = step_gradient(theta, data, lr)
        loss = mse(theta, data)
        if step % 5 == 0:
            print(f"iteration:{step+1},loss:{loss},theta:{theta}")
    return theta

#主函数
def main():
    lr =0.0001  # 学习速率
    theta_init = [1, 2, 1]  # 预设theta初值
    num_iterations = 5000  # 迭代次数

    theta = gradient_descent(dataSet, theta_init, lr, num_iterations)
    loss = mse(theta, normDataSet)
    print(f"Final Loss:{loss},theta0:{theta[0]},theta1:{theta[1]},theta2:{theta[2]}")


if __name__ == '__main__':
    main()