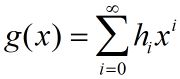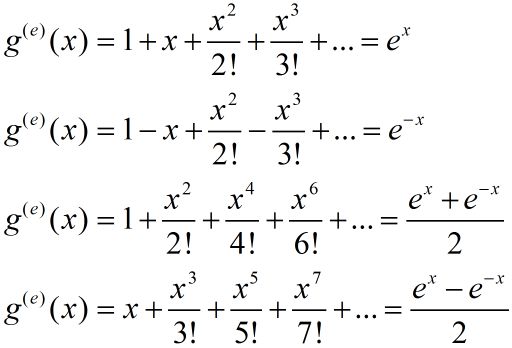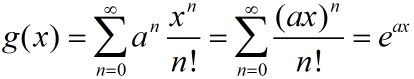组合数学之三 —— 生成函数
前言:我觉得生成函数是一个很玄妙的东西
知识铺垫
我们在这里简单的介绍一下几种为人熟知的数列(给出公式及部分证明):
算术数列,其中的每一项比前一项大一个常数q(等差数列)
几何数列,其中的每一项是前一项的常数q倍(等比数列)
一 . 算术数列
A n = A 0 + n q A_n=A_0+nq An=A0+nq
S n = ( n − 1 ) ∗ A 0 + ( q ∗ n ∗ ( n + 1 ) ) 2 S_n=( n-1 ) * A_0+{( q * n *(n+1)) \over 2} Sn=(n−1)∗A0+2(q∗n∗(n+1))
二 . 几何数列
A n = A 0 ∗ q n A_n=A_0*q^n An=A0∗qn
S n = A 0 ∗ q n − 1 q − 1 − − − > ( q ! = 1 ) Sn=A_0*{ q^n-1 \over q-1 } ---> (q!=1) Sn=A0∗q−1qn−1−−−>(q!=1)
三 . 斐波那契数列
① f ( n ) = f ( n − 1 ) + f ( n − 2 ) ( n > = 2 ) f(n)=f(n-1)+f(n-2) (n>=2) f(n)=f(n−1)+f(n−2)(n>=2)
② f ( 0 ) = 0 , f ( 1 ) = 1 f(0)=0,f(1)=1 f(0)=0,f(1)=1
③ S n = f ( 0 ) + f ( 1 ) + f ( 2 ) + . . . + f ( n ) = f ( n + 2 ) − 1 S_n=f(0)+f(1)+f(2)+...+f(n)=f(n+2)-1 Sn=f(0)+f(1)+f(2)+...+f(n)=f(n+2)−1
我们简单的用归纳法证明一下:
S n + 1 S_{n+1} Sn+1
= f ( 0 ) + f ( 1 ) + f ( 2 ) + . . . + f ( n ) + f ( n + 1 ) =f(0)+f(1)+f(2)+...+f(n)+f(n+1) =f(0)+f(1)+f(2)+...+f(n)+f(n+1)
= [ f ( 0 ) + f ( 1 ) + f ( 2 ) + . . . + f ( n ) ] + f ( n + 1 ) =[f(0)+f(1)+f(2)+...+f(n)]+f(n+1) =[f(0)+f(1)+f(2)+...+f(n)]+f(n+1)
= f ( n + 2 ) − 1 + f ( n + 1 ) =f(n+2)-1+f(n+1) =f(n+2)−1+f(n+1)
= f ( n + 3 ) − 1 =f(n+3)-1 =f(n+3)−1
④ 斐波那契数 f ( n ) f(n) f(n)是偶数当且仅当n能被3整除
⑤ 斐波那契数列通项公式:

⑥ 在帕斯卡三角形从左上到右下的对角线上的二项式系数的和是斐波那契数列

生成函数
简单来说,生成函数是数列的一个副产品:
设
h 0 , h 1 , h 2 , . . . , h n , . . . h_0 , h_1 , h_2 , ... , h_n , ... h0,h1,h2,...,hn,...
是一个无穷数列
ta的生成函数定义为无穷函数:
形式很简单,我们主要通过例题来看一下:
∞ 例一
每一项都是1的无穷数列,ta的生成函数是?
g ( x ) = 1 + x + x 2 + . . . + x n + . . . . = = 1 / ( 1 − x ) g(x)=1+x+x^2+...+x^n+....==1/(1-x) g(x)=1+x+x2+...+xn+....==1/(1−x)
∞ 例二
设 m m m是正整数,二项式系数
C ( m , 0 ) , C ( m , 1 ) , C ( m , 2 ) , . . . , C ( m , m ) C(m,0),C(m,1),C(m,2),...,C(m,m) C(m,0),C(m,1),C(m,2),...,C(m,m)
的生成函数是?
g ( x ) = C ( m , 0 ) + C ( m , 1 ) x + C ( m , 2 ) x 2 + . . . + C ( m , m ) x m g(x)=C(m,0)+C(m,1)x+C(m,2)x^2+...+C(m,m)x^m g(x)=C(m,0)+C(m,1)x+C(m,2)x2+...+C(m,m)xm
根据二项式定理: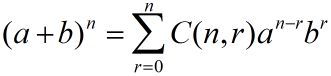
g ( x ) = ( x + 1 ) m g(x)=(x+1)^m g(x)=(x+1)m
注:实际上 m m m为任意实数,都有上式
∞ 例三 (重点)
设 k k k为整数,并设数列 ( h 0 , h 1 , h 2 , h 3 , . . . , h n , . . . ) (h_0,h_1,h_2,h_3,...,h_n,...) (h0,h1,h2,h3,...,hn,...)由令hn等于方程 ( e 1 + e 2 + e 3 + . . . + e k = n ) (e_1+e_2+e_3+...+e_k=n) (e1+e2+e3+...+ek=n)的非负整数解的数目定义?
(建议多读几遍题)
首先我们要搞清楚 h n h_n hn到底是什么:
实际上我们可以将问题看做:有 n n n个1,把ta们分成k份,每一份中允许不含有任何元素
这是隔板法的经典问题:
h n = C ( n + k − 1 , k − 1 ) h_n=C(n+k-1,k-1) hn=C(n+k−1,k−1)
那么 h n h_n hn的生成函数就是:

我们在这里先给出结论:
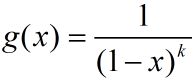
于是我们有:
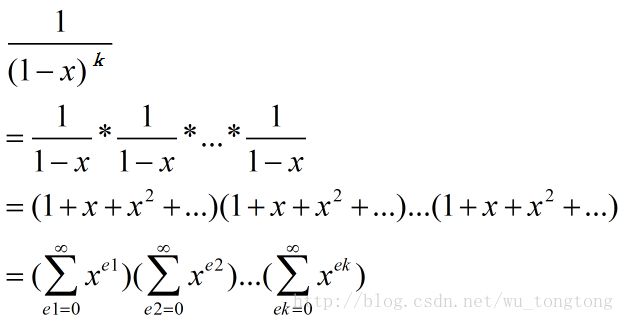
听说你们想知道 1 ( 1 − x ) n 1 \over (1-x)^n (1−x)n1的证明,百度一下
( x + y ) n = ∑ k = 0 n C ( n , k ) x k y n − k (x+y)^n=\sum_{k=0}^{n}C(n,k)x^ky^{n-k} (x+y)n=∑k=0nC(n,k)xkyn−k
( 1 + x ) n = ∑ k = 0 n C ( n , k ) x k (1+x)^n=\sum_{k=0}^{n}C(n,k)x^k (1+x)n=∑k=0nC(n,k)xk
考虑到组合数的性质,上式可以改写为
( 1 + x ) n = ∑ k = 0 ∞ C ( n , k ) x k (1+x)^n=\sum_{k=0}^{∞}C(n,k)x^k (1+x)n=k=0∑∞C(n,k)xk如果指数是负数,则有
( 1 + x ) − n = ∑ k = 0 ∞ C ( − n , k ) x k = ∑ k = 0 ∞ ( − 1 ) k C ( n + k − 1 , k ) x k (1+x)^{-n}=\sum_{k=0}^{∞}C(-n,k)x^k=\sum_{k=0}^{∞}(-1)^kC(n+k-1,k)x^k (1+x)−n=k=0∑∞C(−n,k)xk=k=0∑∞(−1)kC(n+k−1,k)xk我们把 x x x换成 − x -x −x
( 1 + ( − x ) ) − n = ∑ k = 0 ∞ ( − 1 ) k C ( n + k − 1 , k ) ( − x ) k (1+(-x))^{-n}=\sum_{k=0}^{∞}(-1)^kC(n+k-1,k)(-x)^k (1+(−x))−n=k=0∑∞(−1)kC(n+k−1,k)(−x)k= ∑ k = 0 ∞ ( − 1 ) k C ( n + k − 1 , k ) ( − 1 ) k x k = ∑ k = 0 ∞ C ( n + k − 1 , k ) x k =\sum_{k=0}^{∞}(-1)^kC(n+k-1,k)(-1)^kx^k=\sum_{k=0}^{∞}C(n+k-1,k)x^k =k=0∑∞(−1)kC(n+k−1,k)(−1)kxk=k=0∑∞C(n+k−1,k)xk
( 1 − x ) − n = ∑ k = 0 ∞ C ( n + k − 1 , k ) x k = ∑ k = 0 ∞ C ( n + k − 1 , n − 1 ) x k (1-x)^{-n}=\sum_{k=0}^{∞}C(n+k-1,k)x^k=\sum_{k=0}^{∞}C(n+k-1,n-1)x^k (1−x)−n=k=0∑∞C(n+k−1,k)xk=k=0∑∞C(n+k−1,n−1)xk
把 n n n和 k k k交换一下:
( 1 − x ) − k = ∑ n = 0 ∞ C ( k + n − 1 , k − 1 ) x n {(1-x)}^{-k}=\sum_{n=0}^{∞}C(k+n-1,k-1)x^n (1−x)−k=n=0∑∞C(k+n−1,k−1)xn
在上面的记法中, x e i x^{e_i} xei是第i个因子的代表项,于是我们由题意得:
x e 1 ∗ x e 2 ∗ . . . x e k = x n x^{e_1}*x^{e_2}*...x^{e_k}=x^n xe1∗xe2∗...xek=xn
e 1 + e 2 + . . . + e k = n e_1+e_2+...+e_k=n e1+e2+...+ek=n
这样,此生成函数** x n x^n xn的系数**就是n对应的答案
∞ 例四
什么样的数列的生成函数如下式?
( 1 + x + x 2 + x 3 + x 4 + x 5 ) ( 1 + x + x 2 ) ( 1 + x + x 2 + x 3 + x 4 ) (1+x+x^2+x^3+x^4+x^5)(1+x+x^2)(1+x+x^2+x^3+x^4) (1+x+x2+x3+x4+x5)(1+x+x2)(1+x+x2+x3+x4)
设 x e 1 ( 0 < = e 1 < = 5 ) , x e 2 ( 0 < = e 2 < = 2 ) , x e 3 ( 0 < = e 3 < = 4 ) x^{e_1}(0<=e_1<=5) , x^{e_2}(0<=e_2<=2) , x^{e_3}(0<=e_3<=4) xe1(0<=e1<=5),xe2(0<=e2<=2),xe3(0<=e3<=4) 分别表示第一个因子,第二个因子,第三个因子的代表项
假设: e 1 + e 2 + e 3 = n e_1+e_2+e_3=n e1+e2+e3=n
则: x e 1 ∗ x e 2 ∗ x e 3 = x n x^{e_1} * x^{e_2} * x^{e_3}=x^n xe1∗xe2∗xe3=xn
因此乘积中 x n x^n xn的系数是 e 1 + e 2 + e 3 = n e_1+e_2+e_3=n e1+e2+e3=n整数解的个数 h n h_n hn,其中 0 < = e 1 < = 5 , 0 < = e 2 < = 2 , 0 < = e 3 < = 4 0<=e_1<=5 , 0<=e_2<=2 , 0<=e_3<=4 0<=e1<=5,0<=e2<=2,0<=e3<=4 ,当 n > 5 + 2 + 4 = 11 时 , h n = 0 n>5+2+4=11时,h_n=0 n>5+2+4=11时,hn=0
∞ 例五
求装有苹果,香蕉,橘子和梨的果篮的数量 h n h_n hn,
其中在每个果篮中苹果数是偶数,香蕉数是5的倍数,橘子最多拿4个,梨要么不拿,要么只能拿一个
我们要是用组合数学的方法,估计就要光速弃疗了。。。
于是我们用生成函数的角度去考虑:
![]()
![]()
这样我们就使用代数的方法,解决了组合数学问题!
∞ 例六
设{h_n}为方程:{3e_1+4e_2+2e_3+5e_4=n}
的非负整数解得个数。求 h 0 , h 1 , . . . , h n , . . . h_0,h_1,...,h_n,... h0,h1,...,hn,...的生成函数 g ( x ) g(x) g(x)
我们作如下变量替换:
f 1 = 3 ∗ e 1 , f 2 = 4 ∗ e 2 , f 3 = 2 ∗ e 3 , f 4 = 5 ∗ e 4 f_1=3*e_1 , f_2=4*e_2 , f_3=2*e_3 , f_4=5*e_4 f1=3∗e1,f2=4∗e2,f3=2∗e3,f4=5∗e4
则: f 1 + f 2 + f 3 + f 4 = n f_1+f_2+f_3+f_4=n f1+f2+f3+f4=n
其中 f 1 f_1 f1是3的倍数, f 2 f_2 f2是4的倍数, f 3 f_3 f3是2的倍数, f 4 f_4 f4是5的倍数
那我们就可以得到这样的式子:
![]()
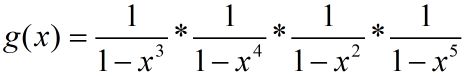
我们在这里提出一个定理:
可以评测的例题
指数生成函数
之前我们利用下面的单项式的集合为数列(h0 , h1 , h2 , h3 …)定义了生成函数:
{ 1 , x , x 2 , x 3 , . . . } \{1,x,x^2,x^3,...\} {1,x,x2,x3,...}
这个生成函数特别适用于某些计数数列,特别是那些涉及二项式系数的数列,这是因为ta有二项式定理的形式
然而,对于某些计数排列的项的数列,更有效的是考虑下面单项式集合的生成函数:
{ 1 , x , x 2 2 ! , x 3 3 ! , x 4 4 ! , . . . } \{1,x,{x^2 \over 2!},{x^3 \over 3!},{x^4 \over 4!},...\} {1,x,2!x2,3!x3,4!x4,...}
这些单项式出现在泰勒级数(e作为数学常数,是自然对数函数的底数):

数列 h 0 , h 1 , h 2 , h 3 , h 4 , . . . h_0,h_1,h_2,h_3,h_4,... h0,h1,h2,h3,h4,...的指数生成函数定义为:

常用指数生成函数的闭形式
这就是知识介绍,很简单明白,我们还是看一些例题:
∞ 例一
设 n n n是正整数,确定下面数列的质数生成函数:
P ( n , 0 ) , P ( n , 1 ) , P ( n , 2 ) , . . . , P ( n , n ) P(n,0),P(n,1),P(n,2),...,P(n,n) P(n,0),P(n,1),P(n,2),...,P(n,n)
其中 P ( n , k ) P(n,k) P(n,k)表示 n n n元素的 k k k排列数目,因此对于 k = 0 , 1 , . . . , n k=0,1,...,n k=0,1,...,n,这个排列的数目是 n ! ( n − k ) ! n! \over (n-k)! (n−k)!n!,因此指数生成函数是:
仔细一看,这 x k x^k xk的系数实际上是 C ( n , k ) C(n,k) C(n,k)
实际上这个生成函数也恰恰是下面数列的普通生成函数:
C ( n , 0 ) , C ( n , 1 ) , C ( n , 2 ) , . . . , C ( n , n ) C(n,0),C(n,1),C(n,2),...,C(n,n) C(n,0),C(n,1),C(n,2),...,C(n,n)
∞ 例二
如果a是任意一个实数,则数列
1 , a , a 2 , a 3 , . . . 1,a,a^2,a^3,... 1,a,a2,a3,...
的指数生成函数是:
这个时候,我们提出一个小问题:
对于正整数 k , k n k,k^n k,kn表示有 k k k种不同类型的对象且每一种对象都有无穷重数的多重集合的 n n n排列数。因此,这个计数数列的指数生成函数就是 e k x e^{kx} ekx
我们在这里再提出一个定理:
设 S S S是多重集合 { n 1 ∗ a 1 , n 2 ∗ a 2 , n 3 ∗ a 3 , . . . , n k ∗ a k } \{ n_1*a_1,n_2*a_2,n_3*a_3,...,n_k*a_k \} {n1∗a1,n2∗a2,n3∗a3,...,nk∗ak}(第 i i i种元素 a i a_i ai有 n i n_i ni个),其中 n i n_i ni是非负整数
设 h n h_n hn是 S S S的 n n n排列数,那么数列 ( h 0 , h 1 , h 2 , . . . , h k ) (h_0,h_1,h_2,...,h_k) (h0,h1,h2,...,hk)的指数生成函数由下式给出:
我们简单的证明一下:
设 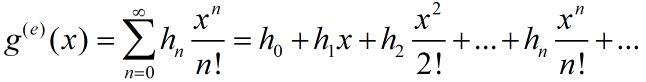
是 ( h 0 , h 1 , h 2 , . . . , h n , . . . ) (h_0,h_1,h_2,...,h_n,...) (h0,h1,h2,...,hn,...)的指数生成函数
注意,当 n > n 1 + n 2 + n 3 + . . . + n k n>n_1+n_2+n_3+...+n_k n>n1+n2+n3+...+nk时 h n = 0 h_n=0 hn=0,所以 g ( x ) g(x) g(x)是有限和
其中: 0 < = m 1 < = n 1 , 0 < = m 2 < = n 2 , 0 < = m 3 < = n 3 , . . . , 0 < = m k < = n k 0<=m_1<=n_1,0<=m_2<=n_2,0<=m_3<=n_3,...,0<=m_k<=n_k 0<=m1<=n1,0<=m2<=n2,0<=m3<=n3,...,0<=mk<=nk
设 n = m 1 + m 2 + . . . + m k n=m_1+m_2+...+m_k n=m1+m2+...+mk,于是上式化为:

因此在①式中 x n n ! x^n \over n! n!xn的系数就是这个玩意。。。
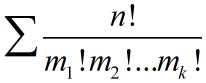
其中的求和就是对所有满足下面条件的 m 1 , m 2 , m 3 , . . . , m k m_1,m_2,m_3,...,m_k m1,m2,m3,...,mk的求和
0 < = m 1 < = n 1 , 0 < = m 2 < = n 2 , 0 < = m 3 < = n 3 , 0 < = m k < = n k 0<=m_1<=n_1,0<=m_2<=n_2,0<=m_3<=n_3,0<=m_k<=n_k 0<=m1<=n1,0<=m2<=n2,0<=m3<=n3,0<=mk<=nk
m 1 + m 2 + m 3 + . . . + m k = n m_1+m_2+m_3+...+m_k=n m1+m2+m3+...+mk=n
对于确定的 m 1 , m 2 , m 3 , . . . , m k m_1,m_2,m_3,...,m_k m1,m2,m3,...,mk, S S S的组合 { m 1 ∗ a 1 , m 2 ∗ a 2 , m 3 ∗ a 3 , . . . , m k ∗ a k } \{m_1*a_1,m_2*a_2,m_3*a_3,...,m_k*a_k\} {m1∗a1,m2∗a2,m3∗a3,...,mk∗ak}的n排列数就是:

显然对于上式的求和,就是原问题的解
原式得证
∞ 例三
设 h n h_n hn表示由数字1,2,3构造的n位数的个数,其中1的个数是偶数,2的个数至少是3,而3的个数至少是4
确定最终的数列 ( h 0 , h 1 , h 2 , . . . , h n , . . . . ) (h_0,h_1,h_2,...,h_n,....) (h0,h1,h2,...,hn,....)的指数生成函数
设 h i ( x ) h_i(x) hi(x)表示对应因子的指数生成函数:
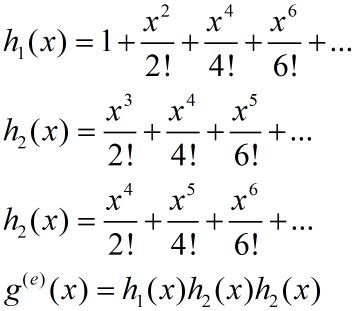
∞ 例四
用红,白,蓝三种颜色给1*n的棋盘着色,要求红色的方格数是偶数,确定给这个棋盘着色的方法数
设 h n h_n hn表示这样的着色数,其中我们定义 h 0 = 1 h_0=1 h0=1
则 h n h_n hn等于有3种颜色(红,白,蓝)的多重集合的n排列数,其中每一种颜色的重数是无穷
且要求红色出现的次数是偶数
我们能过得到一个生成函数(参见上文的定理):
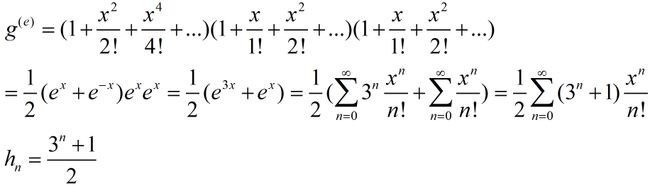
∞ 例五
确定满足下面条件的n位数的个数hn:每个数字都是奇数且数字1和数字3出现偶数次?
设 h 0 = 1 h_0=1 h0=1,数 h n h_n hn等于多重集合 { ∞1,∞3,∞5,∞7,∞*9 }的n排列中1,3出现偶数次的n排列个数
我们可以得到生成函数:
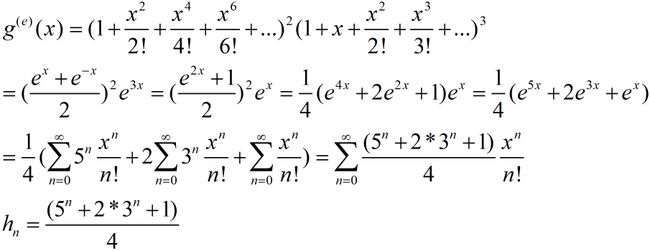
∞ 例六
确定用红,黄,蓝三色给 1 ∗ n 1*n 1∗n棋盘着色中,要求红格数是偶数,且至少有一个蓝格的着色方法数