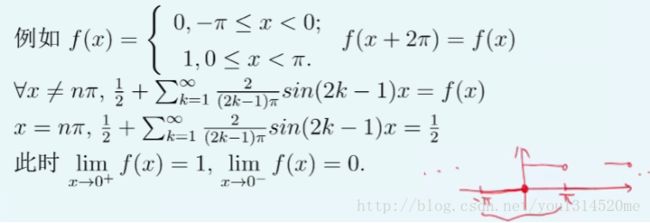清华大学公开课线性代数2——第10讲:傅里叶级数
此博客停止更新迁移至SnailDove’s Blog,查看本文点击此处
笔记源自:清华大学公开课:线性代数2——第10讲:傅里叶级数
**提示:**如果文中图片看不清文字,请右键单击鼠标,选择在新窗口打开图片,然后放大图片(这边上传之前都是可以看清的,由于网页正文部分大小固定,因此图片被自动缩小以便适配网页),截图部分是课堂ppt老师随手的板书。
清华大学线性代数2公开课笔记汇总
第1讲:正定矩阵
第2讲:相似矩阵
第3讲:奇异值分解
第4讲:线性变换1
第5讲:线性变换2
第6讲:伪逆
第7讲:工程中的矩阵
第8讲:图与网络
第9讲:Markov矩阵和正矩阵
第10讲:Fourier级数
第11讲:计算机图像
第12讲:复数与复矩阵
文章目录
- 引言
- 傅里叶级数Fourier series定义
- 定义1
- 定义2
- 定理
- 内积空间inner product space
- 例
- 标准正交系orthonormal system
- 周期函数的傅里叶级数
- 投影
- 关于傅里叶变换的注记
引言
傅里叶级数Fourier series定义
定义1
设 f ( x ) f(x) f(x)是周期为 2 π 2\pi 2π的有限个分段(piecewise)的连续函数( continuous function)(即在 [ π , − π ] [\pi,-\pi] [π,−π]中只有有限个点不连续,且不连续点的左右极限存在),那么它的傅里叶级数是 F = a 0 2 + ∑ k = 1 ∞ ( a k c o s ( k x ) + b k s i n ( k x ) ) , a k = 1 π ∫ − π π f ( x ) c o s ( k x ) d x , b k = 1 π ∫ − π π f ( x ) s i n ( k x ) d x , k = 0 , 1 , … F={a_0\over 2}+\sum\limits_{k=1}^{\infty}(\ a_kcos(kx)+b_ksin(kx)\ ), a_k={1\over \pi}\int_{-\pi}^{\pi}f(x)cos(kx)dx, b_k={1\over \pi}\int_{-\pi}^{\pi}f(x)sin(kx)dx,k=0,1,\ldots F=2a0+k=1∑∞( akcos(kx)+bksin(kx) ),ak=π1∫−ππf(x)cos(kx)dx,bk=π1∫−ππf(x)sin(kx)dx,k=0,1,…,这个级数又称为傅里叶级数的实形式。
f ( x ) f(x) f(x)举例如下的 ( 1 ) (1) (1),而 ( 2 ) (2) (2) 在周期内的不连续点处无极限。

定义2
f ( x ) f(x) f(x)如上,它的傅里叶级数的复形式是 F = ∑ k = − ∞ + ∞ c k e i k x , c k = 1 2 π ∫ − π π f ( x ) e − i k x d x F=\sum\limits_{k=-\infty}^{+\infty}c_ke^{ikx}, c_k={1\over 2\pi}\int_{-\pi}^{\pi}f(x)e^{-ikx}dx F=k=−∞∑+∞ckeikx,ck=2π1∫−ππf(x)e−ikxdx. 推导如下:
在定义1中,使用欧拉公式: e i x = c o s x + i s i n x ⇒ c o s x = e i x + e − i x 2 , s i n x = e i x − e − i x 2 i e^{ix}=cosx+isinx\Rightarrow cosx={e^{ix}+e^{-ix}\over 2},\ sinx={e^{ix}-e^{-ix}\over 2i} eix=cosx+isinx⇒cosx=2eix+e−ix, sinx=2ieix−e−ix ,定义1中的傅里叶级数变成 F = a 0 2 + ∑ k = 1 ∞ [ a k 2 ( e i k x + e − i k x ) − i b k 2 ( e i k x − e − i k x ) ] = a 0 2 + ∑ k = 1 ∞ ( a k − i b k 2 e i k x + a k + i b k 2 e − i k x ) . F={a_0\over 2}+\sum\limits_{k=1}^{\infty}[{a_k\over 2}(e^{ikx}+e^{-ikx})-{ib_k\over 2}(e^{ikx}-e^{-ikx})]={a_0\over 2}+\sum\limits_{k=1}^{\infty}({a_k-ib_k\over 2}e^{ikx}+{a_k+ib_k\over 2}e^{-ikx}). F=2a0+k=1∑∞[2ak(eikx+e−ikx)−2ibk(eikx−e−ikx)]=2a0+k=1∑∞(2ak−ibkeikx+2ak+ibke−ikx). 其中
a k − i b k = 1 2 π ∫ − π π f ( x ) ( e i k x + e − i k x ) d x − i 2 π ∫ − π π f ( x ) e i k x − e − i k x i d x = 1 π ∫ − π π e − i k x d x , a k + i b k = 1 π ∫ − π π e i k x d x a_k-ib_k={1\over 2\pi}\int_{-\pi}^{\pi}f(x)(e^{ikx}+e^{-ikx})dx-{i\over 2\pi}\int_{-\pi}^{\pi}f(x){{e^{ikx}-e^{-ikx}}\over i}dx ={1\over \pi}\int_{-\pi}^{\pi}e^{-ikx}dx,\ a_k+ib_k={1\over \pi}\int_{-\pi}^{\pi}e^{ikx}dx ak−ibk=2π1∫−ππf(x)(eikx+e−ikx)dx−2πi∫−ππf(x)ieikx−e−ikxdx=π1∫−ππe−ikxdx, ak+ibk=π1∫−ππeikxdx , 令 c k = a k − i b k 2 = 1 2 π ∫ − π π f ( x ) e − i k x d x , k = 1 , 2 , … c − k = a k + i b k 2 = 1 2 π ∫ − π π f ( x ) e i k x d x , k = 1 , 2 , … c_k={a_k-ib_k\over 2}={1\over 2\pi}\int_{-\pi}^{\pi}f(x)e^{-ikx}dx,k=1,2,\ldots\quad c_{-k}={a_k+ib_k\over 2}={1\over 2\pi}\int_{-\pi}^{\pi}f(x)e^{ikx}dx,k=1,2,\ldots ck=2ak−ibk=2π1∫−ππf(x)e−ikxdx,k=1,2,…c−k=2ak+ibk=2π1∫−ππf(x)eikxdx,k=1,2,… 这样就得到定义2。注意:正如泰勒级数,这里并没有断言 f ( x ) f(x) f(x)等于它的傅里叶级数。
定理
设 f ( x ) f(x) f(x)是周期为 2 π 2\pi 2π的周期函数, f ( x ) f(x) f(x)和 f ′ ( x ) f'(x) f′(x)均在 [ − π , π ] [-\pi, \pi] [−π,π]上是分段连续的,则 f ( x ) f(x) f(x)的傅里叶级数收敛,且在任意连续点 x = a x=a x=a等于 f ( a ) f(a) f(a),在不连续点 x = a x=a x=a等于 1 2 [ l i m x → a + f ( x ) + l i m x → a − f ( x ) ] {1\over 2}[lim_{x\rightarrow a^{+}}f(x)+lim_{x\rightarrow a^{-}}f(x)] 21[limx→a+f(x)+limx→a−f(x)]。
内积空间inner product space
设 V V V是一个向量空间(线性空间)( R R R或 C C C上), V V V上的一个内积是这样一个函数 (-,-) : V × V → R o r C V\times V\rightarrow R\ or\ C V×V→R or C 满足:
- ∀ u ∈ V , ( u , u ) ≥ 0 \forall u\in V, (u,u)\ge0 ∀u∈V,(u,u)≥0,且若 ( u , u ) = 0 → u = 0 (u,u)=0\rightarrow u=0 (u,u)=0→u=0
- ( c 1 u + c 2 v , w ) = c 1 ( u , w ) + c 2 ( v , w ) , u , v , w ∈ V , c 1 , c 2 ∈ R o r C (c_1u+c_2v,w)=c_1(u,w)+c_2(v,w), u,v,w\in V, c_1,c_2\in R\ or\ C (c1u+c2v,w)=c1(u,w)+c2(v,w),u,v,w∈V,c1,c2∈R or C
- ( u , v ) ‾ = ( v , u ) \overline{(u,v)}=(v,u) (u,v)=(v,u) 共轭对称
注:没有假设 v v v是有限维的。第一条: u u u跟自己的内积必须是一个实数且是一个正数,或者说更确切地是一个非负数,如果 u u u跟自己的内积是等于0的,那么就可以确定 u u u就是 0 0 0向量。第二条:两个向量的线性组合跟另一个向量的内积相当于两个向量跟另一个向量先作内积再做线性组合。第三条: u u u和 v v v的内积与 v v v和 u u u的内积是一个共轭的关系,如果这个函数是定义在 V × V → R V\times V\rightarrow R V×V→R,那么这个内积函数是个对称的, u , v u,v u,v的内积与 v , u v,u v,u的内积是一样的,如果定义在复数上,那么就差一个共轭。
令 ∣ ∣ u ∣ ∣ = ( u , u ) ||u||=\sqrt{(u,u)} ∣∣u∣∣=(u,u),若 ∣ ∣ u ∣ ∣ = 1 ||u||=1 ∣∣u∣∣=1,则 u u u 是一个单位向量。任何一个向量 u ≠ 0 → v ∣ ∣ v ∣ ∣ u\ne 0\rightarrow {v\over ||v||} u̸=0→∣∣v∣∣v是一个单位向量,关于范数( ∣ ∣ ⋅ ∣ ∣ ||·|| ∣∣⋅∣∣),这里范数是长度。
例
- V = R 2 , u = ( a 1 a 2 ) , v = ( b 1 b 2 ) , ( u , v ) = u T v = a 1 b 1 + a 2 b 2 V=R^2,u=\begin{pmatrix}a_1\\a_2\end{pmatrix}, v=\begin{pmatrix}b_1\\b_2\end{pmatrix},(u,v)=u^T v=a_1b_1+a_2b_2 V=R2,u=(a1a2),v=(b1b2),(u,v)=uTv=a1b1+a2b2 是一个内积, ∣ ∣ u ∣ ∣ = ( a 1 2 + a 2 2 ) ||u||=\sqrt{(a_1^2+a_2^2)} ∣∣u∣∣=(a12+a22)。若 V = C 2 V=C^2 V=C2, u , v ∈ C , ( u , v ) = u T v ˉ = a 1 b 1 ‾ + a 2 b 2 ‾ u,v\in C, (u,v)=u^T\bar{v}=a_1\overline{b_1}+a_2\overline{b_2} u,v∈C,(u,v)=uTvˉ=a1b1+a2b2 。
- C [ a , b ] C[a,b] C[a,b]是定义在区间 [ a , b ] [a,b] [a,b]上的全体连续实函数构成的向量空间。定义连续函数的内积为 ( f , g ) = ∫ a b f ( x ) g ( x ) d x (f,g)=\int_{a}^{b}f(x)g(x)dx (f,g)=∫abf(x)g(x)dx 。验证这个式子: f ( x ) ∈ C [ a , b ] , ( f , f ) ≥ 0 f(x)\in C[a,b], (f,f)\ge 0 f(x)∈C[a,b],(f,f)≥0 ,即 ( f , f ) = ∫ a b f ( x ) 2 d x = ∫ a b ∣ f ( x ) ∣ 2 d x ≥ 0 (f,f)=\int_{a}^{b}{f(x)}^2dx=\int_{a}^{b}{|f(x)|}^2dx\ge 0 (f,f)=∫abf(x)2dx=∫ab∣f(x)∣2dx≥0。若 ( f , f ) = 0 (f,f)=0 (f,f)=0,即 ∫ a b ∣ f ( x ) ∣ 2 d x = 0 \int_{a}^{b}{|f(x)|}^2dx=0 ∫ab∣f(x)∣2dx=0,令 F ( t ) = ∫ a t ∣ f ( x ) ∣ 2 d x , a ≤ t ≤ b F(t)=\int_{a}^{t}{|f(x)|}^2dx, a\le t \le b F(t)=∫at∣f(x)∣2dx,a≤t≤b,则 F ( t ) = 0 , F ( t ) F(t)=0, F(t) F(t)=0,F(t)可导, F ′ ( t ) = ∣ f ( t ) ∣ 2 = 0 F'(t)={|f(t)|}^2=0 F′(t)=∣f(t)∣2=0,即 f ( t ) = 0 , t ∈ [ a , b ] f(t)=0,t\in [a,b] f(t)=0,t∈[a,b]。在这里函数的长度的平方定义为函数与自身的内积,即 ∣ ∣ f ( x ) ∣ ∣ 2 = ( f ( x ) , f ( x ) ) = ∫ a b f ( x ) f ( x ) d x ||f(x)||^2=(f(x),f(x))=\int_{a}^{b}f(x)f(x)dx ∣∣f(x)∣∣2=(f(x),f(x))=∫abf(x)f(x)dx。
- 在例2中,若 C [ a , b ] C[a,b] C[a,b]是 [ a , b ] [a,b] [a,b]上的连续复函数的向量空间,则内积定义为: ( f , g ) = ∫ a b f ( x ) g ( x ) ‾ d x (f,g)=\int_{a}^{b}f(x)\overline{g(x)}dx (f,g)=∫abf(x)g(x)dx。
标准正交系orthonormal system
总结:若f(x)在区间 [ a , b ] [a,b] [a,b]存在傅里叶级数,那么f(x)的傅里叶级数是f(x)在标准正交系
{ 1 2 π , 1 π s i n x , 1 π c o s x , 1 π s i n 2 x , 1 π c o s 2 x , … } \{{1\over \sqrt{2\pi}}, {1\over \sqrt{\pi}}sinx, {1\over \sqrt{\pi}}cosx, {1\over \sqrt{\pi}}sin2x, {1\over \sqrt{\pi}}cos2x, \ldots\} {2π1,π1sinx,π1cosx,π1sin2x,π1cos2x,…}下的投影。
周期函数的傅里叶级数
对傅里叶级数的实数形式 F = a 0 2 + ∑ k = 1 ∞ ( a k c o s ( k x ) + b k s i n ( k x ) ) , a k = 1 π ∫ − π π f ( x ) c o s ( k x ) d x , b k = 1 π ∫ − π π f ( x ) s i n ( k x ) d x , k = 0 , 1 , … F={a_0\over 2}+\sum\limits_{k=1}^{\infty}(\ a_kcos(kx)+b_ksin(kx)\ ), a_k={1\over \pi}\int_{-\pi}^{\pi}f(x)cos(kx)dx, b_k={1\over \pi}\int_{-\pi}^{\pi}f(x)sin(kx)dx,k=0,1,\ldots F=2a0+k=1∑∞( akcos(kx)+bksin(kx) ),ak=π1∫−ππf(x)cos(kx)dx,bk=π1∫−ππf(x)sin(kx)dx,k=0,1,…进行变量代换,令 x = π L t , k = n x={\pi\over L}t, k=n x=Lπt,k=n 得:$ dx={\pi\over L}dt,\ t=\cases{L, x=\pi\-L, x=-\pi}\Rightarrow f(t)={a_0\over 2}+\sum\limits_{n=1}^{\infty}[a_ncos({n\pi t\over L})+b_nsin({n\pi t\over L})],\ a_n={1\over L}\int_{-L}^{L}f(t)cos({n\pi t\over L})dt, \b_n={1\over L}\int_{-L}^{L}f(t)sin({n\pi t\over L})dt, n=0,1,\ldots$,对应的复数形式为:
投影
注: e i k x = c o s ( k x ) + i s i n ( k x ) → ( e i k x , e i k x ) = 2 L , L e^{ikx}=cos(kx)+isin(kx)\rightarrow (e^{ikx},e^{ikx})=2L, L eikx=cos(kx)+isin(kx)→(eikx,eikx)=2L,L为半周期的绝对值,另外根据复函数的向量空间的内积定义为: ( f , g ) = ∫ a b f ( x ) g ( x ) ‾ d x → ( f ( x ) , e i k x ) (f,g)=\int_{a}^{b}f(x)\overline{g(x)}dx \rightarrow (f(x),e^{ikx}) (f,g)=∫abf(x)g(x)dx→(f(x),eikx)在周期 [ − π , π ] [-\pi,\pi] [−π,π] 下为 ∫ − π π f ( x ) e − i k s d x \int_{-\pi}^{\pi}f(x)e^{-iks}dx ∫−ππf(x)e−iksdx 。
关于傅里叶变换的注记
Fourier series傅里叶级数和Fourier transformation傅里叶变换是傅里叶分析的主要部分。设 f ( t ) f(t) f(t)周期 T = 2 L T=2L T=2L,则 f ( t ) f(t) f(t)的傅里叶级数展开为 f ( t ) = ∑ k = − ∞ ∞ c k e i k π L t , c k = 1 2 L ∫ − L L f ( t ) e − i k π L t d t f(t)=\sum\limits_{k=-\infty}^{\infty}c_ke^{{ik\pi\over L}t},c_k={1\over 2L}\int_{-L}^{L}f(t)e^{{-ik\pi\over L}t}dt f(t)=k=−∞∑∞ckeLikπt,ck=2L1∫−LLf(t)eL−ikπtdt ( c k c_k ck是 f ( t ) f(t) f(t)在 e i k π L t e^{{ik\pi\over L}t} eLikπt上的投影)。现在考虑定义在 ( − ∞ , + ∞ ) (-\infty, +\infty) (−∞,+∞)上的非周期函数 f ( t ) f(t) f(t),它有傅里叶级数展开形式吗?
给定 L > 0 L>0 L>0,定义KaTeX parse error: Expected 'EOF', got '\cases' at position 8: f_L(t)=\̲c̲a̲s̲e̲s̲{f(t), |t|
当 − L < t < L , f ( t ) = f L ( t ) = F L ( t ) = ∑ k = − ∞ ∞ c k ( L ) e i k π L t , c k ( L ) = 1 2 L ∫ − L L f L ( t ) e − i k π L t d t -L<t<L, f(t)=f_L(t)=F_L(t)=\sum\limits_{k=-\infty}^{\infty}c_k(L)e^{{ik\pi\over L}t},c_k(L)={1\over 2L}\int_{-L}^{L}f_L(t)e^{{-ik\pi\over L}t}dt −L<t<L,f(t)=fL(t)=FL(t)=k=−∞∑∞ck(L)eLikπt,ck(L)=2L1∫−LLfL(t)eL−ikπtdt ,因为 f L ( t ) = 0 , ∣ t ∣ > L → c k ( L ) = 1 2 L ∫ − L L f L ( t ) e − i k π L t d t = 1 2 L ∫ − ∞ ∞ f L ( t ) e − i k π L t d t f_L(t)=0, |t|>L \rightarrow c_k(L)={1\over 2L}\int_{-L}^{L}f_L(t)e^{{-ik\pi\over L}t}dt={1\over 2L}\int_{-\infty}^{\infty}f_L(t)e^{{-ik\pi\over L}t}dt fL(t)=0,∣t∣>L→ck(L)=2L1∫−LLfL(t)eL−ikπtdt=2L1∫−∞∞fL(t)eL−ikπtdt 。由于 k → ∞ k\rightarrow \infty k→∞同时 L → ∞ L\rightarrow \infty L→∞,所以等式右边的指数项未知,因此做变量代换,令 $\tilde{f}L(w)=\int{-\infty}{\infty}f_L(t)e{{-i}wt}dt, $ 令 w k = k π L , w_k={k\pi\over L}, wk=Lkπ, 则 c k ( L ) = 1 2 L f ~ ( k π L ) = 1 2 L f ~ ( w k ) = 1 2 π f ~ ( w k ) ( w k + 1 − w k ) c_k(L)={1\over 2L}\tilde{f}({k\pi\over L})={1\over 2L}\tilde{f}({w_k})={1\over 2\pi}\tilde{f}({w_k})(w_{k+1}-w_k) ck(L)=2L1f~(Lkπ)=2L1f~(wk)=2π1f~(wk)(wk+1−wk)
那么得到傅里叶展开的新形式: f L ( t ) = F L ( t ) = 1 2 π ∑ − ∞ + ∞ f ~ L ( w k ) e i w k t Δ w k , f ~ L ( w ) = ∫ − ∞ + ∞ f L ( t ) e − i w k t d t , Δ w k = w k + 1 − w k = π L f_L(t)=F_L(t)={1\over 2\pi}\sum\limits_{-\infty}^{+\infty}\tilde{f}_L(w_k)e^{iw_kt}\Delta w_k, \tilde{f}_L(w)=\int_{-\infty}^{+\infty}f_L(t)e^{{-i}w_kt}dt, \Delta w_k=w_{k+1}-w_{k}={\pi\over L} fL(t)=FL(t)=2π1−∞∑+∞f~L(wk)eiwktΔwk,f~L(w)=∫−∞+∞fL(t)e−iwktdt,Δwk=wk+1−wk=Lπ。当 L → + ∞ , Δ w → 0 L\rightarrow +\infty, \Delta w\rightarrow 0 L→+∞,Δw→0,等式左边 f L ( t ) f_L(t) fL(t)(一致)趋近于 f ( t ) f(t) f(t),右边就趋近于一个积分形式:$ f(t)={1\over 2\pi}\int_{-\infty}{+\infty}\tilde{f}_L(w)e{iwt}dw , 称 , 称 ,称\tilde{f}(w) 是 是 是f(t) 的 ∗ ∗ 傅 里 叶 变 换 ∗ ∗ , 的**傅里叶变换**, 的∗∗傅里叶变换∗∗,f(t) 是 是 是\tilde{f}(w$)的逆傅里叶变换。
f ( t ) f(t) f(t)实际上是关于时间函数的 s i n c o s sin\ cos sin cos之间叠加出来的,那么 f ~ ( ω ) \tilde{f}(ω) f~(ω)是关于这些频率叠加出来的,它是频率的函数。讲复矩阵的时候将会回到这个傅里叶变换,会考虑傅里叶变换的离散形式,那么 f ( x ) f(x) f(x)或者 f ( t ) f(t) f(t)就被一个向量替换, f ~ ( ω ) \tilde{f}(ω) f~(ω)也被一个向量替换,它们之间互逆的这种傅里叶变换或者逆傅里叶变换的关系,实际上就是通过一个傅里叶矩阵进行互相转换的,以及相应的快速的傅里叶变换。