DOTA_devkit 原理浅析

dota_devkit源码
DOTA dataset
干货 | 目标检测入门，看这篇就够了（已更完）

---

./polyiou.cpp

整个devkit中，最关键的代码之一在文件./polyiou.cpp之中。这个.cpp文件提供了一套高效的对两个任意多边形计算iou（intersection over union）的算法。这为我们在detection阶段实现精确选框提供了帮助。下文开始介绍整个.cpp文件内容及其用到的算法。

1.

const double eps=1E-8;
int sig(double d){
    return(d>eps)-(d<-eps);
}

判断两个浮点数的大小关系，阈值由const double eps=1E-8;确定。

2.

struct Point{
    double x,y; Point(){}
    Point(double x,double y):x(x),y(y){}
    bool operator==(const Point&p)const{
        return sig(x-p.x)==0&&sig(y-p.y)==0;
    }
};

一个结构体，提供一个直角坐标系中点的对象，内置方法有创建以及是否为同一点的判定。

3.

double cross(Point o,Point a,Point b){  //叉积
    return(a.x-o.x)*(b.y-o.y)-(b.x-o.x)*(a.y-o.y);
}

进行一次有向叉积操作，返回三角形OAB的有向面积。面积的正负由向量OA和OB的旋转关系确定，若由OA致OB为逆时针旋转，则为正，反之为负。叉积示意图：

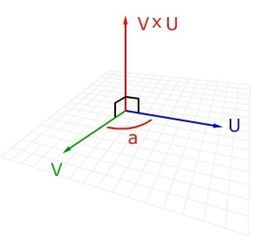
4.

double area(Point* ps,int n){
    ps[n]=ps[0];
    double res=0;
    for(int i=0;i1].y-ps[i].y*ps[i+1].x;
    }
    return res/2.0;
}

参数Point* ps是多边形各顶点坐标，参数int n指定多边形的边数。这里ps[n]=ps[0];是为了下面的循环结构能方便的取到起始点的值。

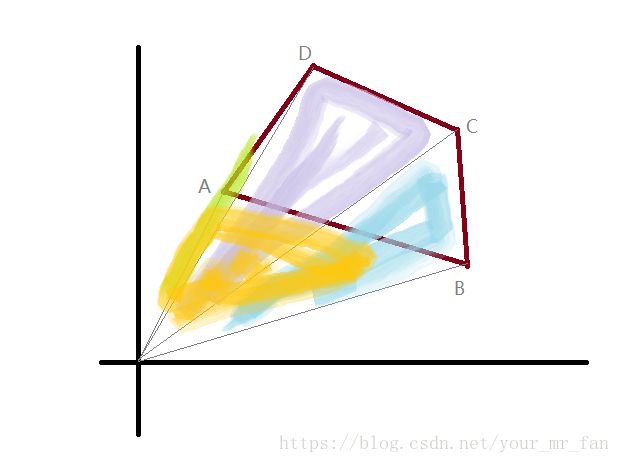
累加结构内部实际上也是一种叉积运算，并将结果依次累加。由于多边形的顶点是按照某一时钟顺序输入的，并且叉积产生的是有向面积，所以以上图求四边形面积为例，最终返回的面积值是 area=△OAB+△OBC+△OCD+△ODC a r e a = △ O A B + △ O B C + △ O C D + △ O D C 。其中 △OAB △ O A B 面积为负， △OBC △ O B C 、 △OCD △ O C D 、 △ODC △ O D C 面积均为正，累加的结果是一个正值（就是说可能为负），也是四边形ABCD的有向面积。

5.

int lineCross(Point a,Point b,Point c,Point d,Point&p){
    double s1,s2;
    s1=cross(a,b,c);
    s2=cross(a,b,d);
    if(sig(s1)==0&&sig(s2)==0) return 2;
    if(sig(s2-s1)==0) return 0;
    p.x=(c.x*s2-d.x*s1)/(s2-s1);
    p.y=(c.y*s2-d.y*s1)/(s2-s1);
    return 1;
}

计算两直线的交点。

6.

//多边形切割
//用直线ab切割多边形p，切割后的在向量(a,b)的左侧，并原地保存切割结果
//如果退化为一个点，也会返回去,此时n为1
void polygon_cut(Point*p,int&n,Point a,Point b){
    static Point pp[maxn];
    int m=0;p[n]=p[0];
    for(int i=0;iif(sig(cross(a,b,p[i]))>0) pp[m++]=p[i];
        if(sig(cross(a,b,p[i]))!=sig(cross(a,b,p[i+1])))
            lineCross(a,b,p[i],p[i+1],pp[m++]);
    }
    n=0;
    for(int i=0;iif(!i||!(pp[i]==pp[i-1]))
            p[n++]=pp[i];
    while(n>1&&p[n-1]==p[0])n--;
}

功能如注释所示。特别的，当切割后的图形边数发生变化时，n的值随之改变。

7.

//返回三角形oab和三角形ocd的有向交面积,o是原点//
double intersectArea(Point a,Point b,Point c,Point d){
    Point o(0,0);
    int s1=sig(cross(o,a,b));
    int s2=sig(cross(o,c,d));
    if(s1==0||s2==0)return 0.0;//退化，面积为0
    if(s1==-1) swap(a,b);
    if(s2==-1) swap(c,d);
    Point p[10]={o,a,b};
    int n=3;
    polygon_cut(p,n,o,c);
    polygon_cut(p,n,c,d);
    polygon_cut(p,n,d,o);
    double res=fabs(area(p,n));
    if(s1*s2==-1) res=-res;return res;
}

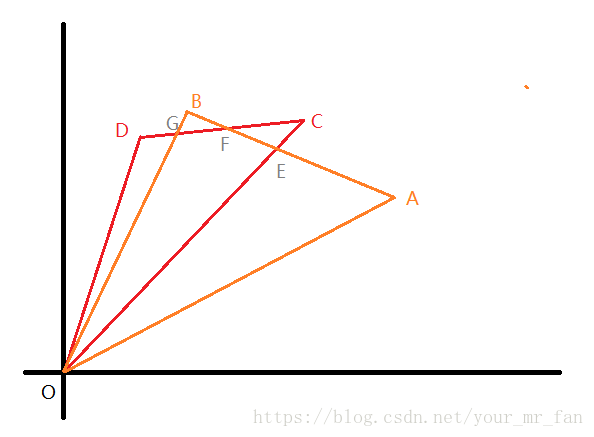
这里的的计算过程是，先将 △OAB △ O A B 和 △OCD △ O C D 的面积方向转为一致为正。之后，把 △OCD △ O C D 的三条边，以逆时针方向，看作三条向量依次对 △OAB △ O A B 及切割后的几何图形切割，以上图为例，切割之后的图形是四边形 OEFG O E F G 。返回值是带有方向的四边形 OEFG O E F G 面积，其正负取决于原始 △OAB △ O A B 和 △OCD △ O C D 的旋转方向是否一致，一致则为正，否则为负。

8.

//求两多边形的交面积
double intersectArea(Point*ps1,int n1,Point*ps2,int n2){
    if(area(ps1,n1)<0) reverse(ps1,ps1+n1);
    if(area(ps2,n2)<0) reverse(ps2,ps2+n2);
    ps1[n1]=ps1[0];
    ps2[n2]=ps2[0];
    double res=0;
    for(int i=0;ifor(int j=0;j1],ps2[j],ps2[j+1]);
        }
    }
    return res;//assumeresispositive!
}

首先处理参数，将两个多边形顶点的旋转方向变为逆时针方向。先证明一个引理：
循环结构的内层循环一次所得的面积是下图粉红区域的面积，符号由包围区域的线段方向决定，若有起始点，则为负，若形成环路，则为正。

for(int j=0;jj++){
        res+=intersectArea(ps1[i],ps1[i+1],ps2[j],ps2[j+1]);
    }

如下图所示

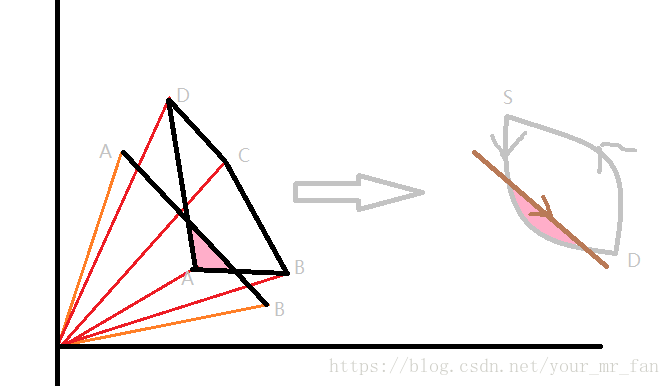
直线 AB A B 是一个多边形的一条边，四边形 ABCD A B C D 是另一个多边形，注意各自的方向。

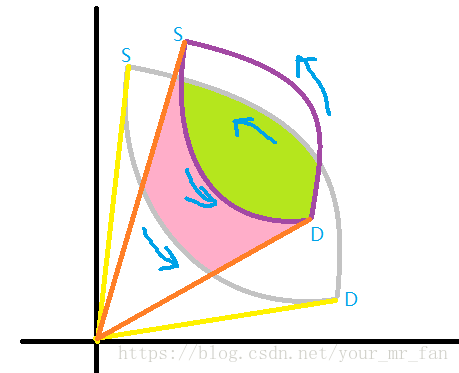
抽象来看，任意多边形，均可以简化为两条曲线的闭环，根据多边形各条边的方向，决定将该线归类至 SD⌢ S D ⌢ 段还是 DS⌢ D S ⌢ 段。外层循环将 SD⌢ S D ⌢ 段中的线段进行完毕后，求得的是粉红颜色区域的面积，负数。再将 DS⌢ D S ⌢ 段中的线段进行完毕后，求得的是绿色+粉红色区域的面积，正数。前后相加可得绿色区域的面积，就是相交面积！注意到，这个面积是非负的。

9.

double iou_poly(vector<double> p, vector<double> q)

这个函数就是将前面的过程整合以下，提供对外的接口。