[深度学习] 自然语言处理---Transformer原理和实现
目录
Encoder-Decoder框架
一 整体架构
动态流程图
二 Encoder
2.1 Encoder Layer和残差网络
Residual Connection
2.2 Attention
Self Attention
Multi-head Attention
2.3 Add & Norm
LayerNormalization 层归一化
2.4 前馈网络 Feed Forward Neural Network
2.5 词向量
Positional Encoding 位置编码
三 Decoder
3.1 Masked Mutil-head Attention
3.2 线性层和softmax
3.3 完整模型代码
四、相关问题
4.1 Transformer为什么需要进行Multi-head Attention?
4.2 Transformer相比于RNN/LSTM,有什么优势?为什么?
4.3 为什么说Transformer可以代替seq2seq?
4.4 Transformer如何并行化的?
4.5 训练-模型的参数在哪里?
参考文献
所谓 ”工预善其事,必先利其器“, BERT之所以取得这么惊才绝艳的效果,很大一部分原因源自于Transformer。为了后面更好、更快地理解BERT模型,这一节从Transformer的开山鼻祖说起,先来跟着”Attention is All You Need[1]“ 这篇文章,走近transformer的世界,在这里你再也看不到熟悉的CNN、RNN的影子,取而代之的是,你将看到Attention机制是如何被发挥的淋漓尽致、妙至毫颠,以及它何以从一个为CNN、RNN跑龙套的配角实现华丽逆袭。对于Bert来说,transformer真可谓天纵神兵,出匣自鸣!
看完本文,你大概能够:
- 掌握Encoder-Decoder框架
- 掌握残差网络
- 掌握BatchNormalization(批归一化)和LayerNormalization(层归一化)
- 掌握Position Embedding(位置编码)
当然,最重要的,你能了解Transformer的原理和代码实现。
Notes: 本文代码参考哈弗大学的The Annotated Transformer
Encoder-Decoder框架
Encoder-Decoder是为seq2seq(序列到序列)量身打造的一个深度学习框架,在机器翻译、机器问答等领域有着广泛的应用。这是一个抽象的框架,由两个组件:Encoder(编码器)和Decoder(解码器)组成。
class EncoderDecoder(nn.Module):
# A standard Encoder-Decoder architecture. Base for this and many other models.
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(EncoderDecoder, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.src_embed = src_embed
self.tgt_embed = tgt_embed
self.generator = generator
def forward(self, src, tgt, src_mask, tgt_mask):
"Take in and process masked src and target sequences."
return self.decode(self.encode(src, src_mask), src_mask,tgt, tgt_mask)
def encode(self, src, src_mask):
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)上述代码呈现了一个标准的Encoder-Decoder框架。在实际应用中,编码器和解码器可以有多种组合,比如(RNN, RNN)、(CNN,RNN)等等,这就是传统的seq2seq框架。后来引入了attention机制,上述框架也被称为”分心模型“。为什么说他”分心“呢?因为对于解码器来说,他在生成每一个单词的时候,中间向量的每一个元素对当前生成词的贡献都是一样的。Attention的思想则是对于当前生成的单词,中间向量z的每个元素对其贡献的重要程度不同,跟其强相关的赋予更大的权重,无关的则给一个很小的权重。
一 整体架构
这部分我们来看看Transformer的架构。Transformer遵循了Encoder-Decoder的架构。在Encoder方面,6个编码器组件协同工作,组成一个大的编码器,解码器同样由6个解码器组件组成。我们先看Encoder。6个编码器组件依次排列,每个组件内部都是由一个多头attention加上一个前馈网络,attenion和前馈的输出都经过层归一化(LayerNormalization),并且都有各自的残差网络 。Decoder呢,组件的配置基本相同, 不同的是Decoder有两个多头attention机制,一个是其自身的mask自注意力机制,另一个则是从Encoder到Decoder的注意力机制,而且是Decoder内部先做一次attention后再接收Encoder的输出。
说完了Encoder和Decoder,再说说输入,模型的输入部分由词向量(embedding)经位置编码(positional Encoding)后输入到Encoder和Decoder。编码器的输出由一个线性层和softmax组成,将浮点数映射成具体的符号输出。
首先,Transformer模型也是使用经典的encoer-decoder架构,由encoder和decoder两部分组成。
上图的左半边用Nx框出来的,就是我们的encoder的一层。encoder一共有6层这样的结构。
上图的右半边用Nx框出来的,就是我们的decoder的一层。decoder一共有6层这样的结构。
输入序列经过word embedding和positional encoding相加后,输入到encoder。
输出序列经过word embedding和positional encoding相加后,输入到decoder。
最后,decoder输出的结果,经过一个线性层,然后计算softmax。
再通俗一点的图,可能你在其他博客里看到的图,如下所示,Transformer由六个编码器和六个解码器组成。
动态流程图
举个例子介绍下如何使用这个Transformer Seq2Seq做翻译
- 首先,Transformer对原语言的句子进行编码,得到memory。
- 第一次解码时输入只有一个
标志,表示句子的开始。 - 解码器通过这个唯一的输入得到的唯一的输出,用于预测句子的第一个词。
编码器通过处理输入序列开启工作。顶端编码器的输出之后会变转化为一个包含向量K(键向量)和V(值向量)的注意力向量集 ,这是并行化操作。这些向量将被每个解码器用于自身的“编码-解码注意力层”,而这些层可以帮助解码器关注输入序列哪些位置合适:
在完成编码阶段后,则开始解码阶段。解码阶段的每个步骤都会输出一个输出序列(在这个例子里,是英语翻译的句子)的元素。
接下来的步骤重复了这个过程,直到到达一个特殊的终止符号,它表示transformer的解码器已经完成了它的输出。每个步骤的输出在下一个时间步被提供给底端解码器,并且就像编码器之前做的那样,这些解码器会输出它们的解码结果 。
第二次解码,将第一次的输出Append到输入中,输入就变成了
二 Encoder
Encoder由N=6个相同的layer组成,layer指的就是上图左侧的单元,最左边有个“Nx”,这里是x6个。
每个Layer由两个sub-layer组成:
- 第一部分是一个multi-head self-attention mechanism
- 第二部分是一个position-wise feed-forward network,是一个全连接层
其中每个sub-layer都加了residual connection和normalisation,因此可以将sub-layer的输出表示为:
def clones(module, N):
"Produce N identical layers."
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
class Encoder(nn.Module):
"Core encoder is a stack of N layers"
def __init__(self, layer, N):
super(Encoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
"Pass the input (and mask) through each layer in turn."
for layer in self.layers:
x = layer(x, mask)
return self.norm(x)以上便是Encoder的核心实现。它由N个encoderLayer组成。输入一次通过每个encoderLayer,然后经过一个归一化层。下面来看下encoderLayer和LayerNorm是什么样子。
我们在每两个子层之间都使用了残差连接(Residual Connection) 和归一化
2.1 Encoder Layer和残差网络
class SublayerConnection(nn.Module):
"""
A residual connection followed by a layer norm.
Note for code simplicity the norm is first as opposed to last.
"""
def __init__(self, size, dropout):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self, x, sublayer):
"Apply residual connection to any sublayer with the same size."
return x + self.dropout(sublayer(self.norm(x)))class EncoderLayer(nn.Module):
"Encoder is made up of self-attn and feed forward (defined below)"
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size
def forward(self, x, mask):
"Follow Figure 1 (left) for connections."
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feed_forward)这里的代码初看上去有点绕,不过没关系,听我娓娓道来。我们先看什么是残差网络(即代码中的SublayerConnection)。其实非常简单,就是在正常的前向传播基础上开一个绿色通道,这个通道里x可以无损通过。这样做的好处不言而喻,避免了梯度消失(求导时多了一个常数项)。最终的输出结果就等于绿色通道里的x加上sublayer层的前向传播结果。注意,这里输入进来的时候做了个norm归一化,关于norm我们后面再说。
Residual Connection
残差连接其实很简单!给你看一张示意图你就明白了:
假设网络中某个层对输入x作用后的输出是F(x),那么增加residual connection之后,就变成了:F(x) + x,这个+x操作就是一个shortcut。那么残差结构有什么好处呢?显而易见:因为增加了一项x,那么该层网络对x求偏导的时候,多了一个常数项1!所以在反向传播过程中,梯度连乘,也不会造成梯度消失!
所以,代码实现residual connection很非常简单:
def residual(sublayer_fn,x):
return sublayer_fn(x)+x
文章开始的transformer架构图中的Add & Norm中的Add也就是指的这个shortcut。
理解了残差网络,EncoderLayer的代码就很好看懂了。sublayer有两个,一个是多头self-attention层,另一个是前馈网络(feed_forward)。输入x先进入多头self-attention,用一个残差网络加成,接着通过前馈网络, 再用一个残差网络加成。
让我们从输入x开始,再从头理一遍这个过程:
- 输入x
- x做一个层归一化: x1 = norm(x)
- 进入多头self-attention: x2 = self_attn(x1)
- 残差加成:x3 = x + x2
- 再做个层归一化:x4 = norm(x3)
- 经过前馈网络: x5 = feed_forward(x4)
- 残差加成: x6 = x3 + x5
- 输出x6
以上就是一个Encoder组件所做的全部工作了。里面有两点暂未说明,一个是多头attention, 另一个是层归一化。
2.2 Self Attention
熟悉attention原理的童鞋都知道,attention可由以下形式表示:
首先说明一下我们的K、Q、V是什么:
- 在encoder的self-attention中,Q、K、V都来自同一个地方(相等),他们是上一层encoder的输出。对于第一层encoder,它们就是word embedding和positional encoding相加得到的输入。
- 在decoder的self-attention中,Q、K、V都来自于同一个地方(相等),它们是上一层decoder的输出。对于第一层decoder,它们就是word embedding和positional encoding相加得到的输入。但是对于decoder,我们不希望它能获得下一个time step(即将来的信息),因此我们需要进行sequence masking。
- 在encoder-decoder attention中,Q来自于decoder的上一层的输出,K和V来自于encoder的输出,K和V是一样的。
- Q、K、V三者的维度一样,即 dq = dk = dv
scaled dot-product attention和dot-product attention唯一的区别就是,scaled dot-product attention有一个缩放因子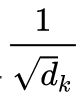
上面公式中的dk表示的是K的维度,在论文里面,默认是64。
那么为什么需要加上这个缩放因子呢?论文里给出了解释:对于dk很大的时候,点积得到的结果维度很大,使得结果处于softmax函数梯度很小的区域。我们知道,梯度很小的情况,这对反向传播不利。为了克服这个负面影响,除以一个缩放因子,可以一定程度上减缓这种情况。
其思想和attention类似,但是self-attention是Transformer用来将其他相关单词的“理解”转换成我们正在处理的单词的一种思路
我们看个例子:
The animal didn't cross the street because it was too tired
这里的 it 到底代表的是 animal 还是 street 呢,对于我们来说能很简单的判断出来,但是对于机器来说,是很难判断的,self-attention就能够让机器把 it 和 animal 联系起来,接下来我们看下详细的处理过程。
Self Attention就是句子中的某个词对于本身的所有词做一次Attention。算出每个词对于这个词的权重,然后将这个词表示为所有词的加权和。每一次的Self Attention操作,就像是为每个词做了一次Convolution操作或Aggregation操作。具体操作如下:
- 首先,self-attention会计算出三个新的向量,在论文中,向量的维度是512维,我们把这三个向量分别称为Query、Key、Value,这三个向量是用embedding向量与一个矩阵相乘得到的结果,这个矩阵是随机初始化的,维度为(64,512)注意第二个维度需要和embedding的维度一样,其值在BP的过程中会一直进行更新,得到的这三个向量的维度是64。
![[深度学习] 自然语言处理---Transformer原理和实现_第9张图片](http://img.e-com-net.com/image/info8/c89b3e38c2974fc5993f43b410ae2bcd.jpg)
-
计算self-attention的分数值,该分数值决定了当我们在某个位置encode一个词时,对输入句子的其他部分的关注程度。这个分数值的计算方法是Query与Key做点成,以下图为例,首先我们需要针对Thinking这个词,计算出其他词对于该词的一个分数值,首先是针对于自己本身即q1·k1,然后是针对于第二个词即q1·k2。
![[深度学习] 自然语言处理---Transformer原理和实现_第10张图片](http://img.e-com-net.com/image/info8/96089c3a55444b26ae52b34d03254834.jpg)
-
接下来,把点成的结果除以一个常数,这里我们除以8,这个值一般是采用上文提到的矩阵的第一个维度的开方即64的开方8,当然也可以选择其他的值,然后把得到的结果做一个softmax的计算。得到的结果即是每个词对于当前位置的词的相关性大小,当然,当前位置的词相关性肯定会会很大。
![[深度学习] 自然语言处理---Transformer原理和实现_第11张图片](http://img.e-com-net.com/image/info8/3c1e87e77670405d90a0395af2de350e.jpg)
-
下一步就是把Value和softmax得到的值进行相乘,并相加,得到的结果即是self-attetion在当前节点的值。
![[深度学习] 自然语言处理---Transformer原理和实现_第12张图片](http://img.e-com-net.com/image/info8/e095003c345e4f7ebc34f8e4bf50196e.jpg)
在实际的应用场景,为了提高计算速度,我们采用的是矩阵的方式,直接计算出Query, Key, Value的矩阵,然后把embedding的值与三个矩阵直接相乘,把得到的新矩阵 Q 与 K 相乘,除以一个常数,做softmax操作,最后乘上 V 矩阵。
归一化之前需要通过除以向量的维度dk来进行标准化,所以最终Self Attention用矩阵变换的方式可以表示为
最终每个Self Attention接受n个词向量的输入,输出n个Aggregated的向量。
这种通过 query 和 key 的相似性程度来确定 value 的权重分布的方法被称为scaled dot-product attention。
上文提到Encoder中的Self Attention与Decoder中的有所不同,Encoder中的Q、K、V全部来自于上一层单元的输出,而Decoder只有Q来自于上一个Decoder单元的输出,K与V都来自于Encoder最后一层的输出。也就是说,Decoder是要通过当前状态与Encoder的输出算出权重后,将Encoder的编码加权得到下一层的状态。
Multi-head Attention
理解了Scaled dot-product attention,Multi-head attention也很简单了。Multi-Head Attention就是将上述的Attention做h遍,然后将h个输出进行concat得到最终的输出。这样做可以很好地提高算法的稳定性,在很多Attention相关的工作中都有相关的应用。
论文提到,他们发现将Q、K、V通过一个线性映射之后,分成 h份,对每一份进行scaled dot-product attention效果更好。然后,把各个部分的结果合并起来,再次经过线性映射,得到最终的输出。这就是所谓的multi-head attention。上面的超参数 h就是heads数量。论文默认是8。
Transformer的实现中,为了提高Multi-Head的效率,将W扩大了h倍,然后通过view(reshape)和transpose操作将相同词的不同head的k、q、v排列在一起进行同时计算,完成计算后再次通过reshape和transpose完成拼接,相当于对于所有的head进行了一个并行处理。
值得注意的是,上面所说的分成 h 份是在 dk,kq,dv 维度上面进行切分的。因此,进入到scaled dot-product attention的 dk 实际上等于未进入之前的 Dk/h
multi-head attention则是通过h个不同的线性变换对Q,K,V进行投影,最后将不同的attention结果拼接起来:
self-attention则是取Q,K,V相同。
论文里面,dmodel = 512,h = 8。所以在scaled dot-product attention里面的
作者同样提到了另一种复杂度相似但计算方法additive attention,在 dk 很小的时候和dot-product结果相似,dk大的时候,如果不进行缩放则表现更好,但dot-product的计算速度更快,进行缩放后可减少影响(由于softmax使梯度过小,具体可见论文中的引用)
这里使用的是点乘attention,而不是加性(additive)attention。但是再提一点,在encoder和decoder的自注意力中,attention层的输入分为self_attn(x, x, x, mask)和self_attn(t, t, t, mask), 这里的x和t分别为source和target输入。后面会看到,从encoder到decoder层的注意力输入时attn(t, m, m), 这里的m是Encoder的输出。
def attention(query, key, value, mask=None, dropout=None):
#因子化的点乘Attention-矩阵形式
#Query: 查询 (batch_size, heads, max_seq_len, d_k)
#Key: 键 (batch_size, heads, max_seq_len_d_k)
#Value: 值 (batch_size, heads, max_seq_len, d_v)
#d_v = d_k
#Q=K=V
d_k = query.size(-1)
# (batch_size, heads, max_seq_len, d_k) * (batch_size, heads, d_k, max_seq_len)
# = (batch_size, heads, max_seq_len, max_seq_len)
# 为了方便说明,只看矩阵的后两维 (max_seq_len, max_seq_len), 即
# How are you
# How [[0.8, 0.2, 0.3]
# are [0.2, 0.9, 0.6]
# you [0.3, 0.6, 0.8]]
# 矩阵中每个元素的含义是,他对其他单词的贡献(分数)
# 例如,如果我们想得到所有单词对单词“How”的打分,取矩阵第一列[0.8, 0.2, 0.3], 然后做softmax
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
# 对于padding部分,赋予一个极大的负数,softmax后该项的分数就接近0了,表示贡献很小
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = F.softmax(scores, dim = -1)
if dropout is not None:
p_attn = dropout(p_attn)
# 接着与Value做矩阵乘法 和V做点积:
# (batch_size, heads, max_seq_len, max_seq_len) * (batch_size, heads, max_seq_len, d_k)
# = (batch_size, heads, max_seq_len, d_k)
context = torch.matmul(p_attn, value)
return context, p_attnclass MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1):
"Take in model size and number of heads."
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0, "heads is not a multiple of the number of the in_features"
# We assume d_v always equals d_k
self.d_k = d_model // h
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
#这里的query, key, value与attention函数中的含义有所不同,这里指的是原始的输入.
#对于Encoder的自注意力来说,输入query=key=value=x
#对于Decoder的自注意力来说,输入query=key=value=t
#对于Encoder和Decoder之间的注意力来说, 输入query=t, key=value=m
#其中m为Encoder的输出,即给定target,通过key计算出m中每个输出对当前target的分数,在乘上m
if mask is not None:
# Same mask applied to all h heads.
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1) Do all the linear projections in batch from d_model => h x d_k
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
# 2) Apply attention on all the projected vectors in batch.
## x: (batch_size, heads, max_seq_len, d_k)
x, self.attn = attention(query, key, value, mask=mask,
dropout=self.dropout)
# 3) "Concat" using a view and apply a final linear.
## x: (batch_size, max_seq_len, d_k*h)
x = x.transpose(1, 2).contiguous() \
.view(nbatches, -1, self.h * self.d_k)
## output: (batch_size, max_seq_len, d_model)
return self.linears[-1](x)def clones(module, N):
"Produce N identical layers."
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])2.3 Add & Norm
在Transformer中,每一个子层(self-attetion,Feed Forward Neural Network)之后都会接一个残缺模块,并且有一个Layer normalization。
一个残差网络,将一层的输入与其标准化后的输出进行相加即可。Transformer中每一个Self Attention层与FFN层后面都会连一个Add & Norm层。
LayerNormalization 层归一化
Normalization有很多种,但是它们都有一个共同的目的,那就是把输入转化成均值为0方差为1的数据。我们在把数据送入激活函数之前进行normalization(归一化),因为我们不希望输入数据落在激活函数的饱和区。
BN的主要思想就是:在每一层的每一批数据上进行归一化。我们可能会对输入数据进行归一化,但是经过该网络层的作用后,我们的数据已经不再是归一化的了。随着这种情况的发展,数据的偏差越来越大,我的反向传播需要考虑到这些大的偏差,这就迫使我们只能使用较小的学习率来防止梯度消失或者梯度爆炸。BN的具体做法就是对每一小批数据,在批这个方向上做归一化。
Layer normalization 它也是归一化数据的一种方式,不过LN 是在每一个样本上计算均值和方差,而不是BN那种在批方向计算均值和方差!公式如下:
class LayerNorm(nn.Module):
"""实现LayerNorm。其实PyTorch已经实现啦,见nn.LayerNorm。"""
def __init__(self, features, eps=1e-6):
"""
Args:
features: 就是模型的维度。论文默认512
eps: 一个很小的数,防止数值计算的除0错误
"""
super(LayerNorm, self).__init__()
self.gamma = nn.Parameter(torch.ones(features))
self.beta = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
"""
Args:
x: 输入序列张量,形状为[B, L, D]
"""
# 在X的最后一个维度求均值,最后一个维度就是模型的维度
mean = x.mean(-1, keepdim=True)
# 在X的最后一个维度求方差,最后一个维度就是模型的维度
std = x.std(-1, keepdim=True)
return self.gamma * (x - mean) / (std + self.eps) + self.beta2.4 前馈网络 Feed Forward Neural Network
我们需要一种方式,把 8 个矩阵降为 1 个,首先,我们把 8 个矩阵连在一起,这样会得到一个大的矩阵,再随机初始化一个矩阵和这个组合好的矩阵相乘,最后得到一个最终的矩阵。
Encoder中和Decoder中经过Attention之后输出的n个向量(这里n是词的个数)都分别的输入到一个全连接层中,完成一个逐个位置的前馈网络。
每个encoderLayer中,多头attention后会接一个前馈网络。这个前馈网络其实是两个全连接层,进行了如下操作:
论文提到,这个公式还可以用两个核大小为1的一维卷积来解释,卷积的输入输出都是dmodel=512dmodel=512 dmodel=512,中间层的维度是dff=2048
class PositionwiseFeedForward(nn.Module):
'''Implements FFN equation.
d_model=512
d_ff=2048
'''
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
# self.w_1 = nn.Conv1d(in_features=d_model, out_features=d_ff, kenerl_size=1)
self.w_2 = nn.Linear(d_ff, d_model)
# self.w_2 = nn.Conv1d(in_features=d_ff, out_features=d_model, kenerl_size=1)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.w_2(self.dropout(F.relu(self.w_1(x))))这两层的作用等价于两个 kenerl_size=1的一维卷积操作。
2.5 词向量
这里就是普通的不能再普通的词向量,将词语变成d_model维的向量。Word embedding应该是老生常谈了,它实际上就是一个二维浮点矩阵,里面的权重是可训练参数,我们只需要把这个矩阵构建出来就完成了word embedding的工作。
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
self.lut = nn.Embedding(vocab, d_model)
self.d_model = d_model
def forward(self, x):
return self.lut(x) * math.sqrt(self.d_model)上面vocab_size就是词典的大小,embedding_size就是词嵌入的维度大小,论文里面就是等于dmodel=512,所以word embedding矩阵就是一个vocab_size*embedding_size的二维张量
Positional Encoding 位置编码
由于Transformer没有用到CNN和RNN,因此,句子单词之间的位置信息就没有利用到。显然,这些信息对于翻译来说是非常有用的,同样一句话,每个单词的意思能够准确的翻译出来,但如果顺序不对,表达出来的意思就截然不同了。举个栗子感受一下,原句:”A man went through the Big Buddhist Temple“, 翻译成:”人过大佛寺“和”寺佛大过人“,意思就完全不同了。
那么如何表达一个序列的位置信息呢?为了解决这个问题,Transformer提出了Positional Encoding的方案,就是给每个输入的词向量叠加一个固定的向量来表示它的位置。文中使用的Positional Encoding如下:
对于某一个单词来说,他的位置信息主要有两个方面:一是绝对位置,二是相对位置。绝对位置决定了单词在一个序列中的第几个位置,相对位置决定了序列的流向。作者利用了正弦函数和余弦函数来进行位置编码:
其中pos是指当前词在句子中的位置,i是指向量中每个值的index,可以看出,在偶数位置,使用正弦编码,在奇数位置,使用余弦编码。
最后把这个Positional Encoding与embedding的值相加,作为输入送到下一层。
其中pos是词在句子中的位置,i是词向量中第i位,即将每个词的词向量为一行进行叠加,然后针对每一列都叠加上一个相位不同或波长逐渐增大的波,以此来唯一区分位置。
其中pos是单词处于句子的第几个位置。我们来考察一下第一个公式,看是否每个位置都能得到一个唯一的值作为编码。为简单起见,不妨令i=0,那么:
我们反过来想,假如存在位置j和k的编码值相同,那么就有:
i,j 为非负整数且i不等于j, 以上两式需要同时满足,可等价为:
i,j为非负整数且i不等于j且k为整数
同时成立,这就意味着:
这显然是不可能的,因为左边是个无理数(无限不循环小数),而右边是个有理数。通过反证法就证明了在这种表示下,每个位置确实有唯一的编码。
上面的讨论并未考虑i的作用。i决定了频率的大小,不同的i可以看成是不同的频率空间中的编码,是相互正交的,通过改变i的值,就能得到多维度的编码,类似于词向量的维度。这里2i<=512(d_model), 一共512维。想象一下,当2i大于d_model时会出现什么情况,这时sin函数的周期会变得非常大,函数值会非常接近于0,这显然不是我们希望看到的,因为这样和词向量就不在一个量级了,位置编码的作用被削弱了。另外,值得注意的是,位置编码是不参与训练的,而词向量是参与训练的。作者通过实验发现,位置编码参与训练与否对最终的结果并无影响。
class PositionalEncoding(nn.Module):
"Implement the PE function."
def __init__(self, d_model, dropout, max_len=5000):
"""初始化。
Args:
d_model: 一个标量。模型的维度,论文默认是512
max_seq_len: 一个标量。文本序列的最大长度
"""
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + Variable(self.pe[:, :x.size(1)],
requires_grad=False)
return self.dropout(x)之所以对奇偶位置分别编码,是因为编码前一个位置是可以由另一个位置线性表示的(公差为1的等差数列),在编码之后也希望能保留这种线性。我们以第1个位置和第k+1个位置为例,还是令i=0:
至此,我们就把Encoder部分的细节介绍完了,下面来看下Decoder部分
三 Decoder
Decoder和Encoder的结构差不多,但是多了一个attention的sub-layer,这里先明确一下decoder的输入输出和解码过程:
- 输出:对应i位置的输出词的概率分布
- 输入:encoder的输出 & 对应i-1位置decoder的输出。所以中间的attention不是self-attention,它的K,V来自encoder,Q来自上一位置decoder的输出
- 解码:这里要特别注意一下,编码可以并行计算,一次性全部encoding出来,但解码不是一次把所有序列解出来的,而是像rnn一样一个一个解出来的,因为要用上一个位置的输入当作attention的query
明确了解码过程之后最上面的图就很好懂了,这里主要的不同就是新加的另外要说一下新加的attention多加了一个mask,因为训练时的output都是ground truth,这样可以确保预测第i个位置时不会接触到未来的信息。
每一个层包括以下3个部分:
- 第一个部分是multi-head self-attention mechanism
- 第二部分是multi-head context-attention mechanism
- 第三部分是一个position-wise feed-forward network
还是和encoder类似,上面三个部分的每一个部分,都有一个残差连接,后接一个Layer Normalization。
但是,decoder出现了一个新的东西multi-head context-attention mechanism。这个东西其实也不复杂,理解了multi-head self-attention你就可以理解multi-head context-attention。
通过观察上面的结构图我们还可以发现Decoder与Encoder的另外一个不同,就是每个Decoder单元的输入层,要先经过一个Masked Attention层。那么Masked的与普通版本的Attention有什么区别呢?
3.1 Masked Mutil-head Attention
mask 表示掩码,它对某些值进行掩盖,使其在参数更新时不产生效果。
Encoder因为要编码整个句子,所以每个词都需要考虑上下文的关系。所以每个词在计算的过程中都是可以看到句子中所有的词的。但是Decoder与Seq2Seq中的解码器类似,每个词都只能看到前面词的状态,所以是一个单向的Self-Attention结构。
Masked Attention的实现也非常简单,只要在普通的Self Attention的Softmax步骤之前,与(&)上一个下三角矩阵M就好了
需要说明的是,我们的Transformer模型里面涉及两种mask。分别是padding mask和sequence mask。其中后者我们已经在decoder的self-attention里面见过啦!其中,padding mask在所有的scaled dot-product attention里面都需要用到,而sequence mask只有在decoder的self-attention里面用到。
所以,我们之前ScaledDotProductAttention的forward方法里面的参数attn_mask在不同的地方会有不同的含义。
-
padding mask
什么是padding mask呢?回想一下,我们的每个批次输入序列长度是不一样的!也就是说,我们要对输入序列进行对齐!具体来说,就是给在较短的序列后面填充0。但是如果输入的序列太长,则是截取左边的内容,把多余的直接舍弃。因为这些填充的位置,其实是没什么意义的,所以我们的attention机制不应该把注意力放在这些位置上,所以我们需要进行一些处理。
具体的做法是,把这些位置的值加上一个非常大的负数(可以是负无穷),这样的话,经过softmax,这些位置的概率就会接近0!
而我们的padding mask实际上是一个张量,每个值都是一个Boolen,值为False的地方就是我们要进行处理的地方。
下面是实现:
# 参考实现代码 def padding_mask(seq_k, seq_q): # seq_k和seq_q的形状都是[B,L] len_q = seq_q.size(1) # `PAD` is 0 pad_mask = seq_k.eq(0) pad_mask = pad_mask.unsqueeze(1).expand(-1, len_q, -1) # shape [B, L_q, L_k] return pad_mask -
Sequence mask
文章前面也提到,sequence mask是为了使得decoder不能看见未来的信息。也就是对于一个序列,在time_step为t的时刻,我们的解码输出应该只能依赖于t时刻之前的输出,而不能依赖t之后的输出。因此我们需要想一个办法,把t之后的信息给隐藏起来。
那么具体怎么做呢?也很简单:产生一个上三角矩阵,上三角的值全为1,下三角的值权威0,对角线也是0。把这个矩阵作用在每一个序列上,就可以达到我们的目的啦。
具体的代码实现如下:
#参考实现代码 def sequence_mask(seq): batch_size, seq_len = seq.size() mask = torch.triu(torch.ones((seq_len, seq_len), dtype=torch.uint8), diagonal=1) mask = mask.unsqueeze(0).expand(batch_size, -1, -1) # [B, L, L] return mask
对于 decoder 的 self-attention,里面使用到的 scaled dot-product attention,同时需要padding mask 和 sequence mask 作为 attn_mask,具体实现就是两个mask相加作为attn_mask。其他情况,attn_mask 一律等于 padding mask。
注意下attention当中的mask。我们之前提到,在三个地方用到了attention。在Encoder的自注意力机制中,mask是用来过滤padding部分的作用,对于source中的每一个词来讲,其他的词对他都是可见的,都可以做出贡献的。但是在Decoder中,mask的作用就有所不同了。这可能又要从Encoder-Decoder框架说起。在这个框架下,解码器实际上可看成一个神经网络语言模型,预测的时候,target中的每一个单词是逐个生成的,当前词的生成依赖两方面:
- 一是Encoder的输出.
- 二是target的前面的单词.
例如,在生成第一个单词是,不仅依赖于Encoder的输出,还依赖于起始标志[CLS];生成第二个单词是,不仅依赖Encoder的输出,还依赖起始标志和第一个单词……依此类推。这其实是说,在翻译当前词的时候,是看不到后面的要翻译的词。由上可以看出,这里的mask是动态的。
def subsequent_mask(size):
"Mask out subsequent positions."
# size: 序列长度
attn_shape = (1, size, size)
# 生成一个上三角矩阵
subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
return torch.from_numpy(subsequent_mask) == 0下面详细介绍下subsequent_mask是如何起作用的。函数的参数size指的是target句子的长度。以”[CLS] That is it“这个长度为4的target输入为例,这个函数的输出是什么呢?
print(subsequent_mask(size=4))
tensor([[[1, 0, 0, 0],
[1, 1, 0, 0],
[1, 1, 1, 0],
[1, 1, 1, 1]]], dtype=torch.uint8)可以看到,输出为一个下三角矩阵,维度为(1,4,4)。现在我们再来看下attention函数,mask起作用的地方是在Query和Key点乘后,结果矩阵的维度为(batch_size, heads, max_seq_len, max_seq_len)。为方便起见,我们只看一条数据,即batch_size=1。进入多头attention时,注意到对mask做了一步操作:
mask = mask.unsqueeze(1)
mask:
tensor([[[[1, 0, 0, 0],
[1, 1, 0, 0],
[1, 1, 1, 0],
[1, 1, 1, 1]]]], dtype=torch.uint8)这时mask的维度变成了(1,1,4,4).
target:
CLS That is it
CLS [[[[0.8, 0.2, 0.3, 0.9]
That [0.2, 0.9, 0.6, 0.4]
is [0.3, 0.6, 0.8, 0.7]
it [1.2, 0.6, 2.1, 3.2]]]]
mask:
[[[[1, 0, 0, 0],
[1, 1, 0, 0],
[1, 1, 1, 0],
[1, 1, 1, 1]]]]写成了上面的样子,mask的作用就很显然了。例如,对于”CLS“来说,预测它下一个词时,只有”CLS“参与了attention,其他的词(相对于CLS为未来的词)都被mask_fill掉了,不起作用。后面的情况依此类推。
细心的小伙伴可能发现了,这里的解释并没有考虑padding部分。事实上,就算加了padding部分(为0),也不影响上述过程,有兴趣的话可以在上面it后面加上个0,下面的矩阵加一列[0 0 0 0 ], 就可以一目了然。
class Decoder(nn.Module):
"Generic N layer decoder with masking."
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)每个组件长什么样子呢?首先输入经过词向量和位置编码,进入target的自注意力层,这里和Encoder一样,也是用了残差和层归一化。然后呢,这个输出再和Encoder的输出做一次context attention,相当于把上面的那层重复了一次,唯一不同的是,这次的attention有点不一样的,不再是自注意力,所有的技术细节都可以参照Encoder部分,这里不再复述。
class DecoderLayer(nn.Module):
"Decoder is made of self-attn, src-attn, and feed forward (defined below)"
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3)
def forward(self, x, memory, src_mask, tgt_mask):
m = memory
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
return self.sublayer[2](x, self.feed_forward)3.2 线性层和softmax
这是整个模型的最后一步了。从Decoder拿到的输出是维度为(batch_size, max_seq_len, d_model)的浮点型张量,我们希望得到最终每个单词预测的结果,首先用一个线性层将d_model映射到vocab的维度,得到每个单词的可能性,然后送入softmax,找到最可能的单词。
线性层的参数个数为d_mode ⋆⋆ vocab_size, 一般来说,vocab_size会比较大,拿20000为例,那么只这层的参数就有512⋆20000512⋆20000个,约为10的8次方,非常惊人。而在词向量那一层,同样也是这个数值,所以,一种比较好的做法是将这两个全连接层的参数共享,会节省不少内存,而且效果也不会差。
class Generator(nn.Module):
"Define standard linear + softmax generation step."
def __init__(self, d_model, vocab):
super(Generator, self).__init__()
self.proj = nn.Linear(d_model, vocab)
def forward(self, x):
return F.log_softmax(self.proj(x), dim=-1)3.3 完整模型代码
def transformer_model(src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h=8, dropout=0.1):
"Helper: Construct a model from hyperparameters."
c = copy.deepcopy
attn = MultiHeadedAttention(h, d_model)
ff = PositionwiseFeedForward(d_model, d_ff, dropout)
position = PositionalEncoding(d_model, dropout)
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
Generator(d_model, tgt_vocab))
# This was important from their code.
# Initialize parameters with Glorot / fan_avg.
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform(p)
return model
model = transformer_model(10, 10, 2)
四、相关问题
4.1 Transformer为什么需要进行Multi-head Attention?
原论文中说到进行Multi-head Attention的原因是将模型分为多个头,形成多个子空间,可以让模型去关注不同方面的信息,最后再将各个方面的信息综合起来。其实直观上也可以想到,如果自己设计这样的一个模型,必然也不会只做一次attention,多次attention综合的结果至少能够起到增强模型的作用,也可以类比CNN中同时使用多个卷积核的作用,直观上讲,多头的注意力有助于网络捕捉到更丰富的特征/信息。
4.2 Transformer相比于RNN/LSTM,有什么优势?为什么?
-
RNN系列的模型,并行计算能力很差。RNN并行计算的问题就出在这里,因为 T 时刻的计算依赖 T-1 时刻的隐层计算结果,而 T-1 时刻的计算依赖 T-2 时刻的隐层计算结果,如此下去就形成了所谓的序列依赖关系。
-
Transformer的特征抽取能力比RNN系列的模型要好。
具体实验对比可以参考:放弃幻想,全面拥抱Transformer:自然语言处理三大特征抽取器(CNN/RNN/TF)比较
但是值得注意的是,并不是说Transformer就能够完全替代RNN系列的模型了,任何模型都有其适用范围,同样的,RNN系列模型在很多任务上还是首选,熟悉各种模型的内部原理,知其然且知其所以然,才能遇到新任务时,快速分析这时候该用什么样的模型,该怎么做好。
4.3 为什么说Transformer可以代替seq2seq?
seq2seq缺点:这里用代替这个词略显不妥当,seq2seq虽已老,但始终还是有其用武之地,seq2seq最大的问题在于将Encoder端的所有信息压缩到一个固定长度的向量中,并将其作为Decoder端首个隐藏状态的输入,来预测Decoder端第一个单词(token)的隐藏状态。在输入序列比较长的时候,这样做显然会损失Encoder端的很多信息,而且这样一股脑的把该固定向量送入Decoder端,Decoder端不能够关注到其想要关注的信息。
Transformer优点:transformer不但对seq2seq模型这两点缺点有了实质性的改进(多头交互式attention模块),而且还引入了self-attention模块,让源序列和目标序列首先“自关联”起来,这样的话,源序列和目标序列自身的embedding表示所蕴含的信息更加丰富,而且后续的FFN层也增强了模型的表达能力,并且Transformer并行计算的能力是远远超过seq2seq系列的模型,因此我认为这是transformer优于seq2seq模型的地方。
4.4 Transformer如何并行化的?
Transformer的并行化我认为主要体现在self-attention模块,在Encoder端Transformer可以并行处理整个序列,并得到整个输入序列经过Encoder端的输出,在self-attention模块,对于某个序列x1,x2,…,xn,self-attention模块可以直接计算xi,xj的点乘结果,而RNN系列的模型就必须按照顺序从x1计算到xn。
4.5 训练-模型的参数在哪里?
Transformer的工作流程就是上面介绍的每一个子流程的拼接
- 输入的词向量首先叠加上Positional Encoding,然后输入至Transformer内
- 每个Encoder Transformer会进行一次Multi-head self attention->Add & Normalize->FFN->Add & Normalize流程,然后将输出输入至下一个Encoder中
- 最后一个Encoder的输出将会作为memory保留
- 每个Decoder Transformer会进行一次Masked Multi-head self attention->Multi-head self attention->Add & Normalize->FFN->Add & Normalize流程,其中Multi-head self attention时的K、V至来自于Encoder的memory。根据任务要求输出需要的最后一层Embedding。
- Transformer的输出向量可以用来做各种下游任务
Encoder端可以并行计算,一次性将输入序列全部encoding出来,但Decoder端不是一次性把所有单词(token)预测出来的,而是像seq2seq一样一个接着一个预测出来的。
transformer的核心点积是没有参数,transformer结构的训练,会优化的参数主要在:
- 嵌入层-Word Embedding
- 前馈(Feed Forward)层
- 多头注意力中的“切片”操作(映射成多个/头小向量)实际是一个全连接层(线性映射矩阵),以及多头输出拼接结果(Concat)后会经过一个Linear全连接层。这两个全连接层也是残差块有意义的地方,如果没有这一层,那这个注意力机制中就没有参数,残差就没有意义了。
GitHub链接:https://github.com/harvardnlp/annotated-transformer
代码解读:Transformer解析与tensorflow代码解读
https://github.com/Kyubyong/transformer
参考文献
- Attention is all your need
- 《Attention is All You Need》浅读(简介+代码)
- Attention机制概念学习笔记
- Attention和Transformer
- 0基础看懂BERT中attention机制的套路
- Attention机制详解(二)——Self-Attention与Transformer
- 最详细的Transformer英文版解释(内涵高清大图)
- Multilingual Hierarchical Attention Networks for Document Classification
- Layer Normalization
- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
- 为什么ResNet和DenseNet可以这么深?一文详解残差块为何有助于解决梯度弥散问题
- Attention?Attention!
- Transformer原理和实现
- 一文看懂Transformer内部原理(含PyTorch实现)
- Building the Mighty Transformer for Sequence Tagging in PyTorch : Part I
- Building the Mighty Transformer for Sequence Tagging in PyTorch : Part II
- Transformer 模型的 PyTorch 实现
- 9012年,该用bert打比赛了
- BERT中文翻译PDF版
- Transformer模型详解
- 图解Transformer(完整版)
- 关于Transformer的若干问题整理记录
-
Transformer各层网络结构详解!面试必备!(附代码实现)
![[深度学习] 自然语言处理---Transformer原理和实现_第1张图片](http://img.e-com-net.com/image/info8/195654fdbd4543d3a976ff7e73437942.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第2张图片](http://img.e-com-net.com/image/info8/380102f640b1463dac3794b18179473e.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第3张图片](http://img.e-com-net.com/image/info8/a752dd4b713842e7af11b806fc47f046.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第4张图片](http://img.e-com-net.com/image/info8/49110fcf4208431eb995f521dd30e665.jpg)
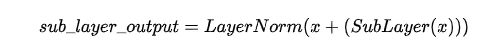
![[深度学习] 自然语言处理---Transformer原理和实现_第5张图片](http://img.e-com-net.com/image/info8/66d0b26f17b649afa1c48e4c8a24389e.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第6张图片](http://img.e-com-net.com/image/info8/555af53d9ed044118777571bb7c8acad.jpg)
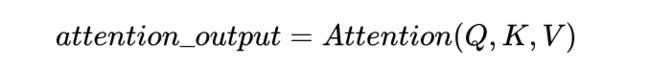
![[深度学习] 自然语言处理---Transformer原理和实现_第7张图片](http://img.e-com-net.com/image/info8/ac728faf07e943ff9aabd14781ecac8b.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第8张图片](http://img.e-com-net.com/image/info8/2b0653b560d94bc693c114550bc78927.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第13张图片](http://img.e-com-net.com/image/info8/70ef6b0b9c9441f89aaa2326f2d341f0.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第14张图片](http://img.e-com-net.com/image/info8/48ec9bc74b194d89bc05ef19b8566fd4.png)
![[深度学习] 自然语言处理---Transformer原理和实现_第15张图片](http://img.e-com-net.com/image/info8/6f2550de88464183a7f934cb84dc06ad.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第16张图片](http://img.e-com-net.com/image/info8/62497d0b7ee6469a87c6bbcee43990fb.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第17张图片](http://img.e-com-net.com/image/info8/2a9f8e83c32043b6be526388c4ddfc25.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第18张图片](http://img.e-com-net.com/image/info8/6b9656b4264644efb298dde2a1bf6e31.jpg)
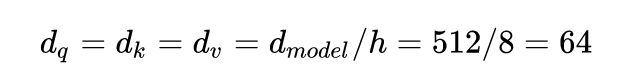
![[深度学习] 自然语言处理---Transformer原理和实现_第19张图片](http://img.e-com-net.com/image/info8/5a446c2f0da34682a15ba2669d7e88f1.jpg)
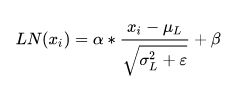
![[深度学习] 自然语言处理---Transformer原理和实现_第20张图片](http://img.e-com-net.com/image/info8/bb60ca161eaf41b78c112764eec7f9ff.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第21张图片](http://img.e-com-net.com/image/info8/e1f0ba09d19344db8afff48d4432c419.jpg)
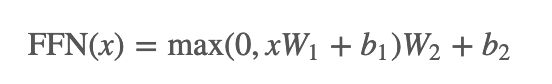
![[深度学习] 自然语言处理---Transformer原理和实现_第22张图片](http://img.e-com-net.com/image/info8/da3a945c19154f70b406b381b7256d1c.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第23张图片](http://img.e-com-net.com/image/info8/bee8e42b5af2426c9a771bcee44fa3e2.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第24张图片](http://img.e-com-net.com/image/info8/b0fe00c2fd0b4d21a8ccd58414c59483.jpg)
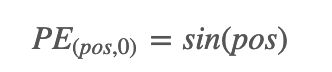
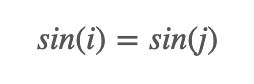
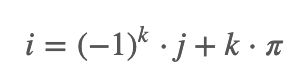
![[深度学习] 自然语言处理---Transformer原理和实现_第25张图片](http://img.e-com-net.com/image/info8/3e98e5b569394e05ac0cca8baa14480c.jpg)
![[深度学习] 自然语言处理---Transformer原理和实现_第26张图片](http://img.e-com-net.com/image/info8/5efb7ad5c2c0429caa5ebd383aeaff58.jpg)