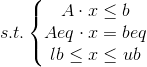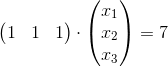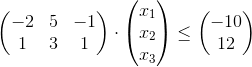MATLAB遗传算法工具箱的使用及实例(线性规划)
一、引言
在使用遗传算法（Genetic Algorithm，GA）之前，你得了解遗传算法是干什么的。遗传算法一般用于求解优化问题。遗传算法最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。
遗传算法的原理和具体流程，各大书籍资料都有，这里不再赘述。我相信来找工具箱的人对原理有所了解。我们在使用工具箱时，不需要理解他的原理，因为这些已经封装到工具箱里了，你只需要设定参数即可。下面来介绍一下MATLAB遗传算法工具箱的使用。
二、线性规划的标准形式
在使用遗传算法求解线性规划问题的时候，需要将模型描述成标准线性规划的形式。
2.1 标准线性规划
标准线性规划使用矩阵的形式表示如下：
是自变量列向量，若有三个自变量，即为
是目标函数
是小于约束中的系数矩阵，
是小于约束常数项的列向量
是等号约束中的系数矩阵，
是等号约束中的常数项的列向量
是的最小取值，
是的最大取值
2.2 非标准线性规划转化为标准线性规划的实例
对于非标准线性规划的形式，如何化为标准型的线性规划呢？下面通过一个例子来说
例如：有以下线性规划问题：
可以观察到，标准型的目标函数是求极小值，而这个案例的目标函数是极大值，我们可以在目标函数
添加一个负号，改为求
，根据中学数学知识可以知道，的最小值，就是的最大值.
在约束条件中，标准型的不等式约束都是小于约束，而案例中出现了大于约束。根据中学知识，不等式的两边同时乘一个负数，不等号改变方向。因此，我们只需要在不等式两边同时乘
即可.
而 
是对于自变量定义域的限制。
因此，上述模型可以转化为：
根据线性代数的知识，约束条件的方程/不等式组可以用矩阵形式表示：
式[1]是等号约束，可表示为
的形式：
， 即 
式[2][3]是小于号的约束，可表示为
的形式：
， 即 
式[4]是自变量的取值范围，可表示为
的形式
， 即
三、遗传算法工具箱的使用说明
MATLAB提供的遗传算法工具箱，主要分为两个函数：gaoptimset()函数和ga()函数，gaoptimset()函数是用于设置遗传算法的一些参数的，可以不设置。若不设置，就使用默认参数。ga()函数是调用遗传算法对优化问题进行计算。
3.1 设置遗传算法的一些参数——gaoptimset()函数的使用
调用格式为: options = gaoptimset('Param1', value1, 'Param2', value2, ...);
其中，'Param1'、'Param2'等是需要设定的参数，比如：种群规模、交叉比例等。value1、value2等则是Param的具体值。常用的参数名如下表（只列出了常用的，还有很多参数可以调整，可自行上网搜索）：
| 设定的参数名(Param名) | 说明 | 默认值 |
| CrossoverFraction | 交叉比例 | 0.8 |
| Generations | 算法中止的最大迭代次数 | 100 |
| PopulationSize | 种群规模 | 20 |
| FitnessLimit | 当适应度函数达到设定的值时算法中止 | - |
| StallGenLimit | 当超过StallGenLimit代适应度函数为改善时，算法中止 | 50 |
例如，需要设置交叉比例为0.7、迭代次数为300、种群规模为30，代码写作（哇，CSDN代码段居然没有MATLAB的高亮，连Octave都没，选个python高亮好了）：
options = gaoptimset('CrossoverFraction', 0.7, 'Generations', 300, 'PopulationSize', 30);返回的options是结构体，用于ga函数的参数
3.2 开始遗传算法的计算——ga()函数的使用
ga函数的调用格式为：
[x_best,fval] = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options);
| 参数名 |
fun | nvars | A | b | Aeq | beq | lb | ub | nonlcon | options |
| 含义 | 目标函数句柄 | 自变量个数 | 线性不等式约束 (以矩阵形式表示，下同) |
线性等式约束 |
自变量的定义域 |
非线性约束需要设置的 | 上一步gaoptimset函数返回的结构体 | |||
| 备注 | 如果某个参数不需要，就设置为空矩阵[] | |||||||||
返回值x_best为取到最小值时的自变量x的取值，fval为所求的最小值。
四、实例
4.1 求下列函数的极小值：![z=2-e^{-(x^{2}+y^{2})}\quad x,y\epsilon [-5,5]](http://img.e-com-net.com/image/info8/7888aeeaea1447d08b7f6594d2b8cfdf.gif){kind=small}
第一步：把目标函数编写成函数的形式，便于调用（将看作
，
看作
）
function z = fitnessfun(x)
% 注意，无论有几个自变量，入口参数都为一个x，表示自变量的矩阵
% 在函数内用x(1)、x(2)等将每个自变量的值索引出来
% 必须以这种格式编写，否则ga函数报错
z = 2 - exp(-(x(1).^2 + x(2).^2));
end第二步：用gaoptimset()函数设置options（ga函数的最后一个参数）
提示：这一步可以跳过，不设置，直接调用ga。
% 根据需要设置，这里我设置种群大小100，交叉概率0.8，迭代500次
options = gaoptimset('PopulationSize',100, 'CrossoverFraction', 0.8, 'Generations', 500);第三步：调用ga()函数，计算出结果
由于本题没有约束，仅对自变量的取值作了限制，因此
均为空矩阵。
自变量的限制为
，因此
，
%% ga函数的参数设置
fun = @fitnessfun; % 设置适应度函数句柄，在定义的函数名前加个@即可
nvars = 2; % 自变量个数，本题为2个自变量
A = []; b = [];
Aeq = []; beq = []; % 没有约束就赋值为空矩阵
lb = [-5; -5]; ub = [5; 5]; % 对自变量x的限制
%% 调用ga函数计算
% 调用格式[x_best,fval] = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options);
% fun是函数句柄， nvars变量数，A,b,Aeq,Beq是线性约束，lb,ub限制X范围，
% nonlcon是非线性约束，做线性规划寻优时赋值为空即可。options是设定参数的结构体
[x_best, fval] = ga(fun, nvars, A,b,Aeq,beq,lb,ub,[],options);
整体代码如下（删除了部分注释，因为没有MATLAB高亮，看的难受）：
clear
clc
% 设置种群大小100，交叉概率0.8，最大进化代数500
options = gaoptimset('PopulationSize',100, 'CrossoverFraction', 0.8, 'Generations', 500);
fun = @fitnessfun; % 设置适应度函数句柄，在定义的函数名前加个@即可
nvars = 2; % 自变量个数，本题为2个自变量
A = []; b = [];
Aeq = []; beq = []; % 没有约束就赋值为空矩阵
lb = [-5;-5]; ub = [5;5]; % 对自变量x的限制
[x_best, fval] = ga(fun, nvars, A,b,Aeq,beq,lb,ub,[],options);
function z = fitnessfun(x)
z = 2-exp(-(x(1).^2+x(2).^2));
end
得到fval的值为1，即为所求。
4.2 求下列函数的最小值
本题的等式约束为：
，因此：
，
，
不等式(小于)约束为
，因此
，
自变量的约束为 
，因此
准备工作做完后，开始编程：
第一步，编写目标函数：
function z = fitnessfun(x)
z = (x(2)-x(1).^2).^2 + (1-x(1)).^2 + (x(3) - x(2).^2).^2 + (1 - x(2)).^2;
end第二步，调用ga函数进行求解
为减小篇幅，这里就不设置遗传算法的相关参数了，不调用gaoptimset()，使用默认参数，感兴趣的读者可以自行设置。
fun = @fitnessfun; % 设置适应度函数句柄
nvars = 3; % 自变量个数
A = [-10,-20,-1;1,2,4]; b = [-100;40]; % A·x <= b约束
Aeq = [9,6,1]; beq = [100]; % Aeq·x <= beq约束
lb = [2;2;2]; ub = [10;10;10]; % 定义域lb <= x <= ub
[x_best, fval] = ga(fun, nvars, A,b,Aeq,beq,lb,ub,[],[]);
运行代码，得到fval的值约为2330.8681，即为所求。
由于遗传算法具有一定的随机性，因此每次求解的结果可能有些许差别。
线性规划的遗传算法求解就到这里，感谢观看！