《Digital Integrated Circuits》读后笔记(二)

本文仅作个人娱乐分享，请勿用作其他用途

chapter 5 The CMOS Inverter

1. inverter gate

• cost
• static behavior
• dynamic response
• energy and power consumption

2. The Static CMOS inverter

MOS: when $|V_{GS}<V_T|$ , the off-resistance is infinite

​ when $|V_{GS}>V_T|$ , the on-resistance is finite

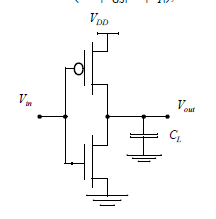
Ideal Features:

• when $V_{in}$ is high, NMOS is on, PMOS is off. $V_{out}$ is 0.

  when $V_{in}$ is low, NMOS is off, PMOS is on. $V_{out}$ is $V_{DD}$.

  Swing is from $V_{DD}$ and $GND$ . logic level is not dependent upon the relative device sizes.

• steady state: finite resistance between output and $V_{DD}$ or $GND$ . No current flow, no static power.

• input resistance is extremely high. Theoretically, inverter can have an infinite fan-out.

  However, increasing fan-out will increase the propagation delay.

---

VTC(voltage-transfer characteristic):

a narrow transition zone.

---

Transient behavior:

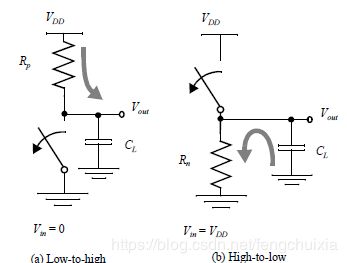
output capacitance of the gate, $C_L$

composed of drain diffusion capacitances of NMOS and PMOS transistors, the capacitance of the connecting wires, the input capacitance of fan-out gates.

response time: time constant $R_p{C}_L$.

Conclusion: A fast gate is built by keeping the output capacitance small or by decreasing the on-resistance of the transistor.

---

Robustness: static CMOS converter is insensitive to these variations

3. The switching threshold of CMOS inverter $V_M$

noise margin $V_{IH}$ and $V_{IL}$

switching threshold $V_M$ is defined as the point where $V_{in}=V_{out}$.

Supposed the supply voltage is high and the velocity-saturated appear:

$$V_M=\frac{r{V}_{DD}}{1+r}$$ ($V_{DD}$ is high) $r=\frac{k_p{V}_{DSATp}}{k_n{V}_{DSATn}}=\frac{{\upsilon }_{satp}{W}_p}{{\upsilon }_{satn}{W}_n}$

if $V_M$ located at mid, $r=1$, and $(W/L{)}_p=(W/L{)}_n\times (V_{DSATn}{k}_n^{’}/V_{DSATp}{k}_p^{{}^{\prime }})$

if $V_M$ is required high, then $r>1$, make PMOS wider

Analysis:

• $V_M$ - $W_p/W_n$ : $V_M$ is insensitive to the ratio. So we can set the width of the PMOS transistor to values smaller than those required for symmetry.
• If required asymmetrical transfer characteristics, then we can change the ratio.

4. Noise margin $N{M}_H$and $N{M}_L$:

$V_{IH}$ and $V_{IL}$ :operational points of the inverter where $\frac{d{V}_{out}}{d{V}_{in}}=-1$. $g=-1$.

$$g=\frac{1+r}{(V_M-V_{Tn}-V_{DSATn}/2)({\lambda }_n-{\lambda }_p)}$$ $g$ is determined by channel length modulation.

5. Scaling the supply voltage

$g$ is inverse ratio with $V_M$. And $V_M$ is proportional with $V_{DD}$ if $r$ is fixed.

So if $g$ increases when $V_{DD}$ decreases.(Supposed)

However:

• reducing the supply voltage is detrimental to the performance on the gate.
• dc-characteristic becomes increasingly sensitive to variations in the device parameters such as transistor threshold when supply voltage is comparable with threshold.
• reducing the signal swing. More sensitive to external noise.

Examples:

At around 100 mV, gain in transition-region approaches 1. And VTC is detoriated.

Conclusion:

$$V_{DDmin}>2...4{\varphi }_T$$ , if we want a low $V_{DD}$, we need to reduce the temperature.

If $V_{DD}$ is under threshold, $$g=-(\frac{1}{n})(e^{V_{DD}/2{\varphi }_T}-1)$$.

6. The Dynamic behavior

* Only here we discuss the dynamic behavior

Capacitances:

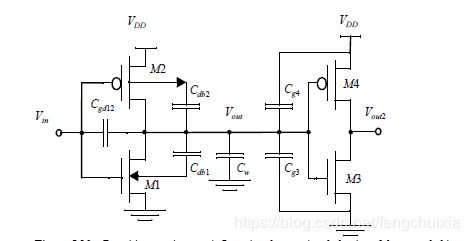
Supposed $V_{in}$ has an ideal input voltage source.

• Gate-Drain Capacitance $C_{gd12}$

  during the first half, $M1$ is cut-off or saturation mode. The channel capacitance does not play a role here. If cut-off, it is between gate and bulk, if saturation, it is between gate and source. The capacitance is mainly the overlap capacitance.

  Miller effect the capacitance-to-ground must have a value that is twice as large as the floating capacitance.

  $C_{gd}=2C_{GD0}W$ $C_{GD0}$ is the overlap capacitance per unit width

• Diffusion Capacitance $C_{db1}$ and $C_{db2}$

  the capacitance between drain and bulk.

• Wiring Capacitance $C_w$

  connecting wires

• Gate Capacitance $C_{g3}$ and $C_{g4}$

  fanout capacitance $C_{fanout}=C_{gate}(NMOS)+C_{gate}(PMOS)=$

  $(C_{GSOn}+C_{GDOn}+W_n{L}_n{C}_{ox})+(C_{GSOp}+C_{GDOp}+W_p{L}_p{C}_{ox})$

  The total channel capacitance is not constant actually. varies from $2/3WL{C}_{ox}$ to the full $WL{C}_{ox}$.

---

Propagation Delay :

$t_p={\int }_{v_1}^{v_2}\frac{C_L(x)}{i(v)}dv$

$$R_{eq}=\frac{3}{4}\frac{V_{DD}}{I_{DSAT}}(1-\frac{7}{9}\lambda V_{DD})$$ $R_{eq}$ is the average on-resistance of the MOS transistor.

$t_{pHL}=In(2)R_{eqn}{C}_L=0.69R_{eqn}{C}_L$

$t_{pLH}=0.69R_{eqp}{C}_L$

$t_p=(t_{pHL}+t_{pLH})/2=0.69C_L(R_{eqn}+R_{eqp})/2$

$R_{eqn}$ and $R_{eqp}$ is the normalized on-resistances. $(\frac{W}{L})$ is ratio. the realistic resistance is $R_{eqn}/(W/L)$.

If we want $R_{eqn}==R_{eqp}$ , then PMOS is wider than NMOS. However, $t_{pHL}=t_{pLH}$ does not mean $t_p$ is smallest. We can make PMOS smaller than computation

Another computation: ignore the factor $\lambda$

$t_{pHL}=\frac{3}{4}\frac{V_{DD}}{I_{DSATn}}\approx 0.52\frac{C_L}{(W/L{)}_n(k_n{)}^{’}{V}_{DSATn}}$

If $V_{DD}$ decreases, $t_{pHL}$ will increases.

---

Conclusion:

• Reduce $C_L$

• Increase the (W/L) ratio

• Increase $V_{DD}$

7）Design for Performance

Supposed symmetrical inverter:

$C_L=C_{int}+C_{ext}$

$t_p=0.69R_{eq}(C_{int}+C_{ext})=0.69R_{eq}{C}_{int}(1+C_{ext}/C_{int})=t_{p0}(1+C_{ext}/C_{int})$

$t_{p0}$ is unloaded delay

$C_{int}=S{C}_{iref}$ $R_{eq}=R_{ref}/S$ $S$ is the sizing factor. $C_{iref}$ is a minimize-sized inverter.

$t_p=0.69R_{iref}{C}_{iref}(1+\frac{C_{ext}}{S{C}_{iref}})=t_{p0}(1+\frac{C_{ext}}{S{C}_{iref}})$

Conclusion:

if $S$ is larger, $t_p$ is smaller.

8. A Chain of Inverter

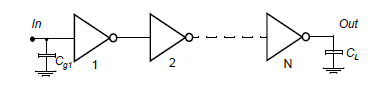
$C_{int}=\gamma C_g$ $\gamma$ is a proportionality factor. close to 1.

$t_p=t_{p0}(1+\frac{C_{ext}}{r{C}_g})=t_{p0}(1+f/\gamma )$ $f$ is effective fanout.

$t_{p,j}=t_{p0}(1+\frac{C_{g,j+1}}{\gamma C_{g,j}})=t_{p0}(1+\frac{f_j}{\gamma })$

$t_p=\sum _{j=0}^N{t}_{p,j}=t_{p0}\sum _{j=0}^N(1+\frac{C_{g,j+1}}{\gamma C_{g,j}})$ $C_{g,N+1}=C_L$

To make $t_p$ min, we need each inverter is sized up by the same factor $f$.

$f=\sqrt[N]{C_L/C_{g,1}}=\sqrt[N]{F}$ $t_p=N{t}_{p0}(1+\sqrt[N]{F}/\gamma )$

The optimized $f$:

if $\gamma$ equals 1, $f$ is chose to be 3.6.If $f$ is too small, which means $N$ is too large, then $t_p$ will be larger.

---

If the input signal changes gradually, PMOS and NMOS conduct simultaneously.

$t_s$-$t_p$: $t_p$ increases linearly with $t_s$

So we can change $t_p$ : ${t_p}^i={t_{step}}^i+\eta {t_{step}}^{i-1}$

8. Dynamic Power Consumption:

$$E_{VDD}=C_L{V_{DD}}^2$$

$$E_{out}=\frac{C_L{V_{DD}}^2}{2}$$

Half energy has been dissipated by PMOS

Conclusion: $E_{dissipated}=C_L{V_{DD}}^2$

$$P_{dyn}=C_L{V_{DD}}^2{f}_{0->1}$$ $f_{0->1}=2t_p$ means a switched time.(on and off)

However:

switching factor $f_{0->1}$ $P_{dyn}=C_L{V_{DD}}^2{P}_{0->1}f=C_{EFF}{V_{DD}}^{2}f$ $f$ is clock time

$C_{EFF}$ effective capacitance

Solution: How to reduce power

• Reducing $V_{DD}$ But $V_{DD}$ need to be larger than 2$V_T$, or the performance is bad.
• Reducing the effective capacitance

---

Analysis:

$t_p=t_{p0}((1+f/\gamma )+(1+F/f\gamma ))$

$t_{p0}$~$\frac{V_{DD}}{V_{DD}-V_{TE}}$

$V_{TE}=V_t+V_{DSATn}/2$

Conclusion: Energy & Performance

if $F$ is larger, the optimal sizing factor for energy is smaller than the one for performance.

9. Direct-Path Currents

$E_{dp}=V_{DD}\frac{I_{peak}{t}_{sc}}{2}+V_{DD}\frac{I_{peak}{t}_{sc}}{2}=t_{sc}{V}_{DD}{I}_{peak}$

$P_{dp}=t_{sc}{V}_{DD}{I}_{peak}f=C_{sc}{V_{DD}}^{2}f$

$t_{sc}=\frac{V_{DD}-2V_T}{V_{DD}}{t}_s$

$t_{sc}$ represents the time both devices are conducting.

$t_s$ represents the 0-100% transition time.

If we want to decrease the direct-path dissipation, we need to make $t_p$ larger.

10. Static consumption

$P_{stat}=I_{stat}{V}_{DD}$ $I_{stat}$ is a leakage current

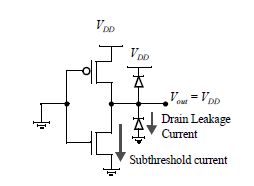
• subtheshold current solution: SOI
• drain leakage current

11. Put it all together

$P_{tot}=P_{dyn}+P_{dp}+P_{stat}$

---

PDP power-delay product: $PDP=P_{av}{t}_p$ average energy consumed per switching event

$PDP=C_L{V_{DD}}^2{f}_{max}{t}_p=\frac{C_L{V_{DD}}^2}{2}$

switching event means 0->1 or 1->0 transition

$E_{av}$ is twice the PDP

---

EDP energy-delay product: combine a measure of performance and energy

$EDP=\frac{C_L{V_{DD}}^2}{2}{t}_p$

High supply voltage reduce delay, but harm the energy

---

Conclusion:

$V_{DDopt}=\frac{3}{2}{V}_{TE}$

12. Scaling technology

The interconnect component