Unity三维数学 ——— 向量Vector、三角函数

一、Unity 中的向量

1、向量的长度

public class sc03 : MonoBehaviour 
{
	// Update is called once per frame
	void Update () {
        Demo1();
	}

    void Demo1()
    {
        // 获取当前物体的空间坐标
        Vector3 pos1 = transform.position;

        //计算当前向量模长的三种方法
        float m01 = Mathf.Sqrt(Mathf.Pow(pos1.x, 2) + Mathf.Pow(pos1.y, 2) + Mathf.Pow(pos1.z, 2));//Method1
        float m02 = pos1.magnitude;//Method2-----Unity Provide
        float m03 = Vector3.Distance(Vector3.zero, pos1);//Method3

        Debug.LogFormat("{0}-----{1}-----{2}", m01, m02, m03);
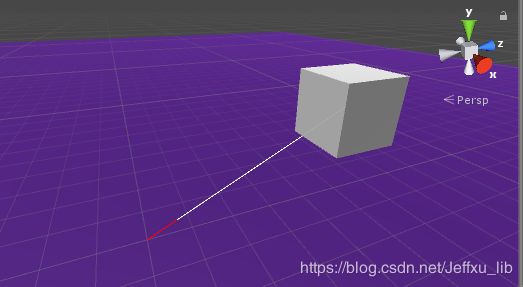
        Debug.DrawLine(Vector3.zero, pos1,Color.red); //在原点到物体之间划红色的线
    }
}

效果如下图所示

 

2、向量的归一化处理（即向量的方向）

public class sc03 : MonoBehaviour 
{
	// Update is called once per frame
	void Update () {
        Demo1();
	}

    void Demo1()
    {
        // 获取当前物体的空间坐标
        Vector3 pos1 = transform.position;

        // 通过公式来对向量进行归一化处理
        Vector3 n01 = pos1 / pos1.magnitude;
        // 通过Unity的API来对向量进行归一化处理
        Vector3 n02 = pos1.normalized;

        Debug.DrawLine(Vector3.zero, pos1); //原点到物体间划线
        Debug.DrawLine(Vector3.zero, n01,Color.red);//原点到归一化后的向量之间划线

    }
}

结果如下所示

 

3、向量的运算（求两点的方向）：

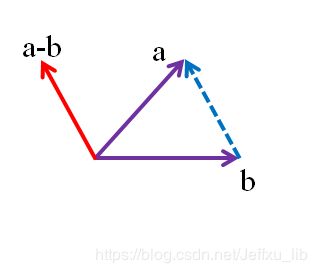
（1）、在Unity中的两个向量相减的结果，如下图的a向量减b向量，所得到的结果并不在虚线处，而是实线处。因为它是从世界坐标原点作为起点的，相当于将所减的结果由虚线平移到坐标原点处。两个向量相减的结果一定是与这两个向量共起点（即世界坐标系的原点）。在Unity中  的结果是如下图红色箭头所指的点。

 

（2）、在Unity中用代码展示如下：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class OperVector : MonoBehaviour 
{
    public Transform tf0, tf1, tf2, tf3;
    void Start () {
        tf0 = GameObject.Find("Sphere").GetComponent();//位于坐标原点：黑色的球
        tf1 = GameObject.Find("Sphere1").GetComponent();//蓝色的球
        tf2 = GameObject.Find("Sphere2").GetComponent();//紫色的球
        tf3 = GameObject.Find("Sphere3").GetComponent();	//白色的球
	}
	
	// Update is called once per frame
	void Update () {
        Demo01();
	}
    /// 

    /// 向量的方向
    /// 
    void Demo01()
    {
        //dir01 相当于两个向量相减之后的点
        Vector3 dir01 = tf1.position - tf2.position;
        //该向量的方向为：坐标原点到dir01
        Debug.DrawLine(tf0.position, dir01,Color.red);

        Debug.DrawLine(tf0.position, tf1.position,Color.yellow);
        Debug.DrawLine(tf0.position, tf2.position,Color.yellow);
        Debug.DrawLine(tf1.position, tf2.position,Color.red);

        Debug.DrawLine(tf3.position, dir01,Color.blue);

    }
}

结果如下

 

（3）、将一个向量平移到另一个地方，但方向依然保持不变。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Move : MonoBehaviour 
{
    Transform s1, s2, s3, s4;
    Vector3 v1;
    Vector3 v2;
    Vector3 leftv1,leftv2;

    void Start () {
        s1 = GameObject.Find("Sphere1").GetComponent();
        s2 = GameObject.Find("Sphere2").GetComponent();
        s3 = GameObject.Find("Sphere3").GetComponent();
        s4 = GameObject.Find("Sphere4").GetComponent();      
		
	}

    private void Update()
    {
        // v1只表示s1到s2的向量，其长度固定，但起点位于世界坐标系的原点
        v1 = s2.position - s1.position;
        // v2只表示s2到s3的向量，其长度固定，起点位于世界坐标系的原点
        v2 = s3.position - s2.position;

        // leftv1相当于将向量v1平移到s4位置处，即方向大小保持不变，起点位于s4处。
        leftv1 = s4.position + v1;
        leftv2 = leftv1 + v2;


        Debug.DrawLine(s1.position, s2.position, Color.red);
        Debug.DrawLine(s2.position, s3.position, Color.yellow);

        Debug.DrawLine(s4.position, leftv1, Color.red);
        Debug.DrawLine(leftv1, leftv2, Color.yellow);
    }

}

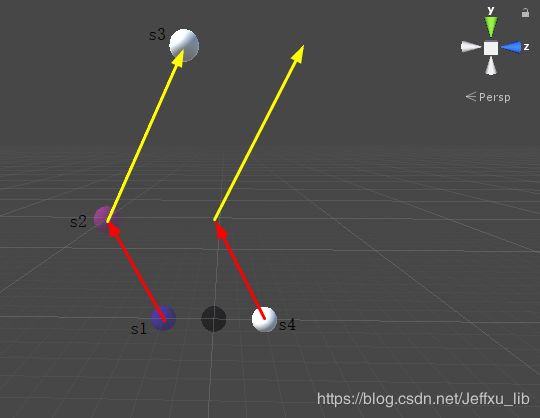
运行结果如下

  

---

二、向量的运算

1、向量的基本操作

Vector3 a, b;
//向量a[0]，a[1]，a[2]分别表示a.x , a.y , a.z
a[0] = a[1] = a[2] = 10;

Vector3.Angle(a, b); //返回向量a,b间的夹角，结果为度
Vector3.Cross(a, b); //向量a,b叉乘
Vector3.Dot(a, b); //向量a,b点乘

// MoveTowards 是从一个点按指定的速度匀速的移动到另一个点，可以看到移动的过程。
transform.position = Vector3.MoveTowards(this.transform.position, new Vector3(0, 0, 10),0.1f);

2、点乘与叉乘及求角度

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class OperVector : MonoBehaviour 
{
    private Transform tf0, tf1, tf2, tf3;
    float angle01;


    void Start () {
        tf0 = GameObject.Find("Sphere").GetComponent();//位于坐标原点：黑色的球
        tf1 = GameObject.Find("Sphere1").GetComponent();//蓝色的球
        tf2 = GameObject.Find("Sphere2").GetComponent();//紫色的球
        tf3 = GameObject.Find("Sphere3").GetComponent();	//白色的球
	}

	void Update () {
        Demo02();
	}
    void Demo01()
    {
        Debug.DrawLine(tf0.position, tf1.position,Color.yellow);
        Debug.DrawLine(tf0.position, tf2.position,Color.yellow);

        //两向量点乘
        float resultOfDot = Vector3.Dot(tf1.position, tf2.position);

        /*由点乘结果求两向量的夹角时，必须先对两向量归一化处理，或者最后除以两向量模长的乘积再求反余弦
         * 1、此时求的角是两向量间的最小夹角
         * 2、所求的角度没有正负之分，只能看大小
         * 3、对于标准化过的向量，方向完全相同，点乘结果为1，相反为-1
         * 4、角度的范围是：0——180度之间
        */
        float resultOfDot01 = Vector3.Dot(tf1.position.normalized, tf2.position.normalized);
        angle01 = Mathf.Acos(resultOfDot01) * Mathf.Rad2Deg;
               
    }

    void Demo02()
    {
        Debug.DrawLine(tf0.position, tf1.position, Color.yellow);
        Debug.DrawLine(tf0.position, tf2.position, Color.yellow);

        //求两向量的叉乘
        Vector3 resultOfCross = Vector3.Cross(tf1.position, tf2.position);
        Debug.DrawLine(Vector3.zero, resultOfCross,Color.red);

        //用叉乘来求两向量的夹角：叉乘求角度的范围是：0——90 度。
        Vector3 resultOfCross01 = Vector3.Cross(tf1.position.normalized, tf2.position.normalized);
        float angle02 = Mathf.Asin(resultOfCross01.magnitude) * Mathf.Rad2Deg;


        //结合点乘和叉乘，可以计算一圈的夹角
        /* 当叉乘大于0时，两向量的夹角小于180度；
         * 当叉乘小于0时，两向量的夹角大于180度。
        */
        if (resultOfCross.y<0)
        {
            float angle03 = 360 - angle01;

        }

    }

}

 

---

三、Unity 中三角函数的角度表示

//角度到弧度转换
float d = 60;  //60度
float r1 = d * Mathf.PI / 180;
float r2 = d * Mathf.Deg2Rad;

//弧度到角度
float r = 3;
float d1 = r * 180 / Mathf.PI;
float d2 = r * Mathf.Rad2Deg;