中国国家队清华集训 2012-2013 第一天 BZOJ 2957 楼房重建 线段树题解

2957: 楼房重建

Time Limit: 10 Sec Memory Limit: 256 MB
Submit: 2065 Solved: 986

---

Description

　　小A的楼房外有一大片施工工地，工地上有N栋待建的楼房。每天，这片工地上的房子拆了又建、建了又拆。他经常无聊地看着窗外发呆，数自己能够看到多少栋房子。
　　为了简化问题，我们考虑这些事件发生在一个二维平面上。小A在平面上(0,0)点的位置，第i栋楼房可以用一条连接(i,0)和(i,Hi)的线段表示，其中Hi为第i栋楼房的高度。如果这栋楼房上任何一个高度大于0的点与(0,0)的连线没有与之前的线段相交，那么这栋楼房就被认为是可见的。
　　施工队的建造总共进行了M天。初始时，所有楼房都还没有开始建造，它们的高度均为0。在第i天，建筑队将会将横坐标为Xi的房屋的高度变为Yi(高度可以比原来大—修建，也可以比原来小—拆除，甚至可以保持不变—建筑队这天什么事也没做)。请你帮小A数数每天在建筑队完工之后，他能看到多少栋楼房？

---

Input

　　第一行两个正整数N,M
　　接下来M行，每行两个正整数Xi,Yi

---

Output

　　M行，第i行一个整数表示第i天过后小A能看到的楼房有多少栋

---

Sample Input

3 4

2 4

3 6

1 1000000000

1 1

---

Sample Output

1

1

1

2

---

数据约定

　　对于所有的数据1<=Xi<=N，1<=Yi<=10^9

N,M<=100000

---

HINT

Source

中国国家队清华集训 2012-2013 第一天

---

题解：

显然是一个线段树问题（233好像也不是很显然）
（其实也可以分块做，分块真是好东西）
下面来讲是怎么利用线段树来维护的
首先我们观察这样一张图

不好意思放错了
首先我们来观察这样一张图

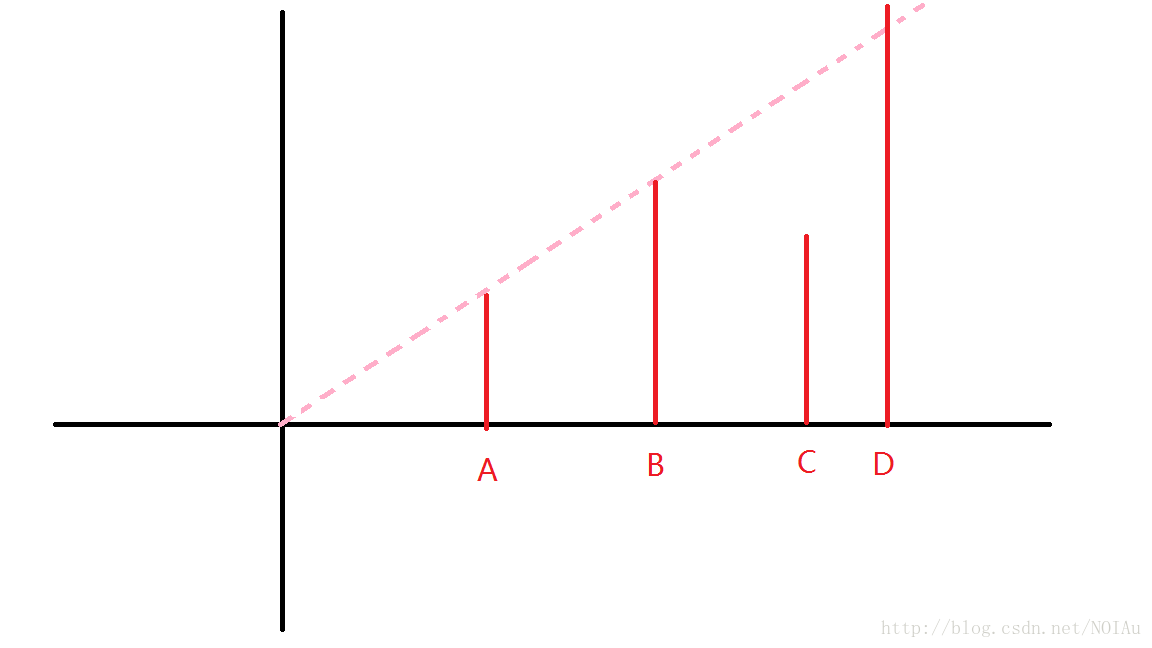
我们从原点看过去，可以发现只能看到A和D，也就是说虽然B比A高，但是我们不一定能够看到B，搞清楚这一点之后，我们开始进行维护，首先明确一点，如果我们对每个点（x）作为线段树中的叶子节点的话，那么，有一点是显然的，我们既然要维护区间可加性，就要让答案在 node[1].cnt 中，其中 cnt 表示这个区间里的答案是多少，什么意思呢？对于一个线段树的节点，比如我们一共是1到100的区间，那么我们在考虑51到100的子区间的时候，直接忽略1到50的所有楼房，就像没有了一样，这样就可以维护区间可加性了，我们发现一件显然的事情…线段树的操作还可以有很多，而不仅仅局限于我所学的那么点…（我太菜了）
维护的时候我们发现更改一个点的值，只会对后面的造成影响，而不会对前面的造成影响，（即使我变矮了，也是前面的那个高于我了的影响了我），所以左边的信息是不会变的，所以我们处理右边的信息即可
其中modify函数是这样的

//对于一个线段树中的一个点（表示一段区间），我们定义val为该区间的点和原点相连形成的直线的斜率最大值
void modify(int loc,double val,int l,int r,int rt){
    if(l==r){
        node[rt].cnt=1;//cnt表示这个区间（此时已经是一个点，可以被看到，其他被忽视）
        node[rt].val=val;//该区间最大值为该点的val
        return;
    }
    int mid=(l+r)>>1;
    if(loc<=mid) modify(loc,val,l,mid,rt<<1);
    else         modify(loc,val,mid+1,r,rt<<1|1);//递归修改
    node[rt].val=max(node[rt<<1].val,node[rt<<1|1].val);
    node[rt].cnt=node[rt<<1].cnt+cal(node[rt<<1].val,mid+1,r,rt<<1|1);//注意这一步操作，我们马上会讲到cal函数
    //node[rt]的cnt值应该等于左侧的cnt值（因为无论右边的情况是怎样，左边的cnt值均不会被改变），然后计算右边的cal值，其中其决定性影响的应该是左边区间的斜率最大的房屋
}

具体操作我们这里多的一个 cal 函数的实现是这样的：

int cal(double val,int l,int r,int rt){
    if(l==r) return node[rt].val>val;//如果已经递归到底层叶子节点，那么如果该点的斜率大于左侧区间（也是一个点）最大的斜率，则可以被看到，返回1，反之返回0
    int mid=(l+r)>>1;
    if(node[rt<<1].val<=val) return cal(val,mid+1,r,rt<<1|1);   //观察代码下面的图片①
    else return node[rt].cnt-node[rt<<1].cnt+cal(val,l,mid,rt<<1);
}

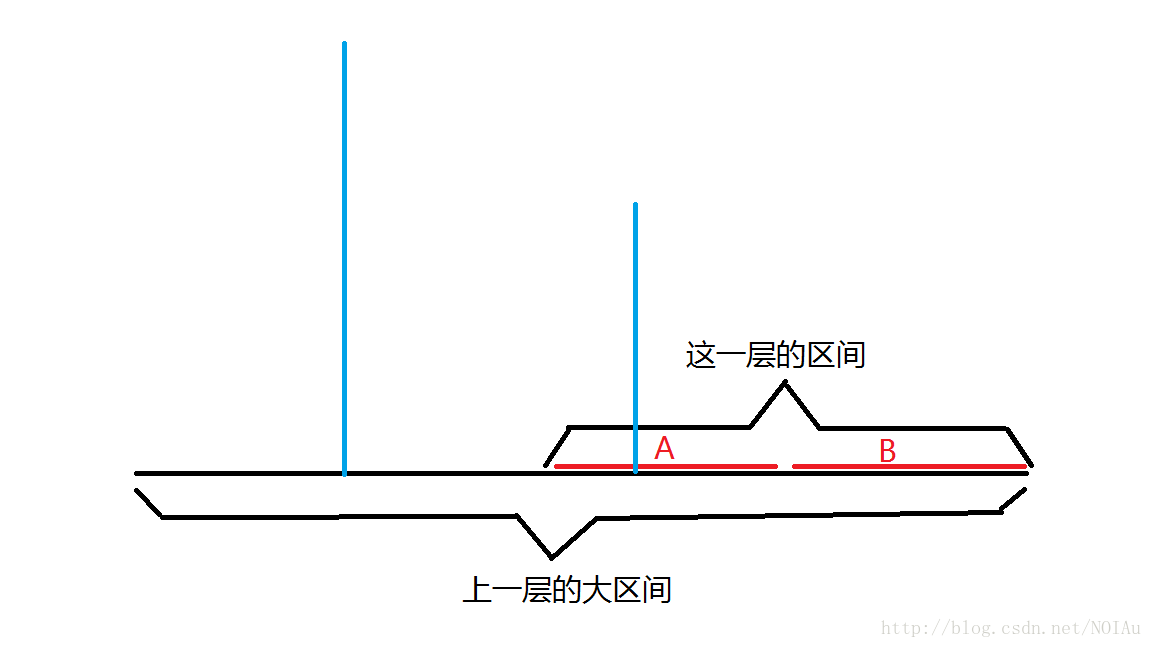
如果上一层的左边的最大值传过来之后，发现这一层的左区间A中的最大值小于上一层左区间的最大值，那么这一层的左区间一定没有贡献，所以直接cal右区间

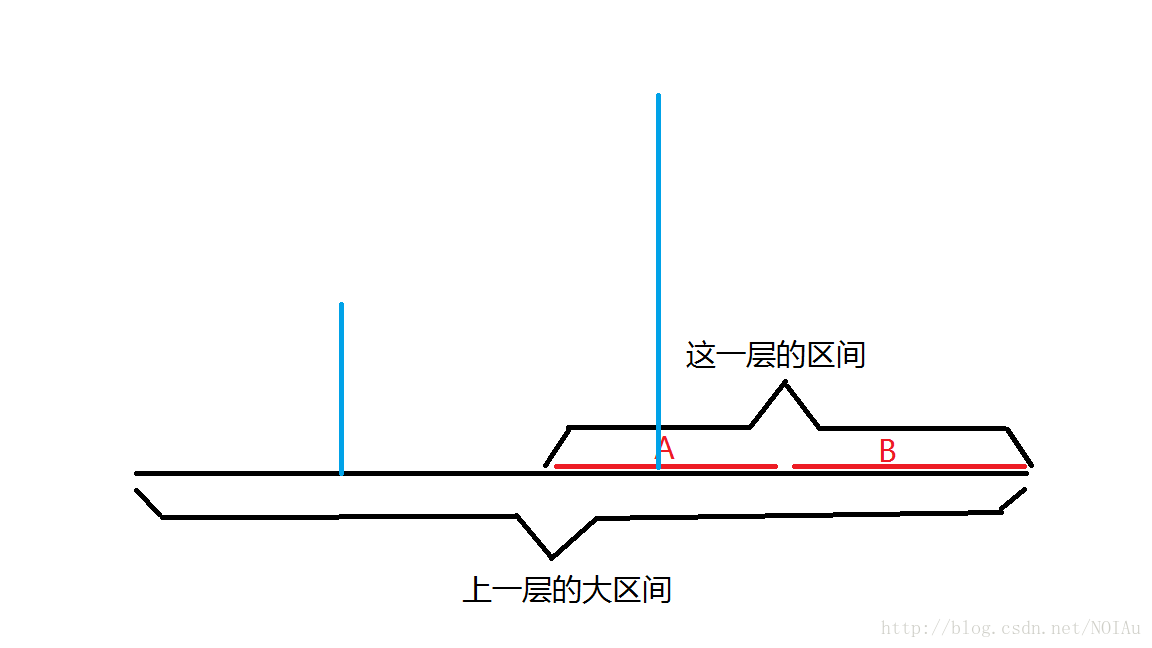
对于另一种情况，这一层的左区间对答案有贡献，所以我们只需要计算新的左区间的贡献，因为这一层的右区间的某些建筑如果被这一层的左区间的某些建筑挡住了，那么因为这一层的左区间的最大值比上一层的左区间的最大值大，所以上一层的左区间不会对已经计算出的右区间的情况更改

#include
#include
#include
#define root 1 
using namespace std;
int readin(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,m,x,y;
struct data{
    int cnt;
    double val;
}node[400005];

int cal(double val,int l,int r,int rt){
    if(l==r) return node[rt].val>val;
    int mid=(l+r)>>1;
    if(node[rt<<1].val<=val) return cal(val,mid+1,r,rt<<1|1);
    else return node[rt].cnt-node[rt<<1].cnt+cal(val,l,mid,rt<<1);
}
void modify(int loc,double val,int l,int r,int rt){
    if(l==r){
        node[rt].cnt=1;
        node[rt].val=val;
        return;
    }
    int mid=(l+r)>>1;
    if(loc<=mid) modify(loc,val,l,mid,rt<<1);
    else         modify(loc,val,mid+1,r,rt<<1|1);
    node[rt].val=max(node[rt<<1].val,node[rt<<1|1].val);
    node[rt].cnt=node[rt<<1].cnt+cal(node[rt<<1].val,mid+1,r,rt<<1|1);
}
int main(){
    n=readin();m=readin();
    for(register int i=1;i<=m;i++){
        x=readin();y=readin();
        modify(x,(double)(y*1.0/x),1,n,1);
        printf("%d\n",node[root].cnt); 
    }
    return 0;
}