Romberg(龙贝格)积分法
变长梯形法方法简单,但精度低而且收敛速度慢。如果在保留这种方法使用的逐步二分思想的基础上,将用误差事后估计法所求得的误差作为积分近似值的补偿值,以便进一步提高精度,同时又引入加速收敛的技术,则就可以得到一种更加完善的数值积分方法,即Romberg积分法。
将 T 2 n T_{2n} T2n和 T n T_n Tn的表达式代入 I ‾ = 4 3 T 2 n − 1 3 T n \overline I=\frac{4}{3}T_{2n}-\frac{1}{3}T_n I=34T2n−31Tn,得:
I ‾ = 4 3 ( 1 2 ⋅ 1 2 H [ f ( a ) + f ( b ) + 2 ∑ k = 1 n − 1 f ( x k ) ] + 1 2 H ∑ k = 0 n − 1 f ( x k + 1 2 ) ) − 1 3 ( 1 2 H [ f ( a ) + f ( b ) + 2 ∑ k = 1 n − 1 f ( x k ) ] ) \overline I = \frac{4}{3}(\frac{1}{2}·\frac{1}{2}H[f(a)+f(b)+2\sum_{k=1}^{n-1}f(x_k)]+\frac{1}{2}H\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}})) \\-\frac{1}{3}(\frac{1}{2}H[f(a)+f(b)+2\sum_{k=1}^{n-1}f(x_k)]) I=34(21⋅21H[f(a)+f(b)+2k=1∑n−1f(xk)]+21Hk=0∑n−1f(xk+21))−31(21H[f(a)+f(b)+2k=1∑n−1f(xk)])
I ‾ = 1 2 H ( f ( a ) + 4 ∑ k = 0 n − 1 f ( x k + 1 2 ) + 2 ∑ k = 1 n − 1 f ( x k ) + f ( b ) ) = S n \overline I =\frac{1}{2}H(f(a)+4\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}})+2\sum_{k=1}^{n-1}f(x_k)+f(b))=S_n I=21H(f(a)+4k=0∑n−1f(xk+21)+2k=1∑n−1f(xk)+f(b))=Sn
所以
S n = 4 3 T 2 n − 1 3 T n S_n=\frac{4}{3}T_{2n}-\frac{1}{3}T_n Sn=34T2n−31Tn
由此可得到结论一:用变步长梯形法二分前、后所求得的两个积分值 T n T_n Tn和 T 2 n T_{2n} T2n进行线性组合,即可得到用复化Simpson公式计算的积分值 S n S_n Sn。
进一步考察复化Simpson公式。其截断误差与步长H的4次方成正比,即:
I − S 2 n I − S n ≅ 1 16 \frac{I-S_{2n}}{I-S_n} \cong \frac{1}{16} I−SnI−S2n≅161
整理得:
I − S 2 n = 1 15 ( S 2 n − S n ) I-S_{2n}=\frac{1}{15}(S_{2n}-S_n) I−S2n=151(S2n−Sn)
同理有:
C n = 16 15 S 2 n − 1 15 S n C_n=\frac{16}{15}S_{2n}-\frac{1}{15}S_n Cn=1516S2n−151Sn
由此得到结论二:用变步长 S i m p s o n Simpson Simpson公式二分前、后所求得的两个积分值 S n S_n Sn和 S 2 n S_{2n} S2n进行线性组合,即可得到用复化Cotes公式计算的积分值 C n C_n Cn。
再考察复化Cotes公式。其截断误差与步长H的6次方成正比,即:
I − C 2 n I − C n ≅ 1 64 \frac{I-C_{2n}}{I-C_n}\cong \frac{1}{64} I−CnI−C2n≅641
整理得:
R n = 64 63 C 2 n − 1 63 C n (2) R_n=\frac{64}{63}C_{2n}-\frac{1}{63}C_n \tag{2} Rn=6364C2n−631Cn(2)
由此得到结论三:用变步长 C o t e s Cotes Cotes公式二分前、后所求得的两个积分值 C n C_n Cn和 C 2 n C_{2n} C2n进行线性组合,即可得到Romberg公式计算的积分值 R n R_n Rn,并称式(2)为Romberg公式。
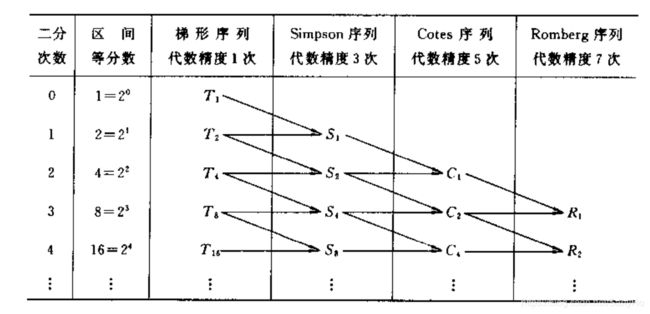
将变步长(区间数加倍、步长减半)梯形法的积分近似值通过线性组合得到变步长Simpson法的积分近似值,再将变步长Simpson法的积分近似值通过线性组合得到变步长Cotes法的积分近似值,再将变步长Cotes法的积分近似值通过线性组合得到变步长Romberg法的积分近似值。这种逐次二分积分区间并利用线性组合的加速方法将一个粗糙的积分值 T n T_n Tn序列逐步加工成精度较高的积分值 R n R_n Rn序列的方法,称为Romberg积分法。
Romberg积分法的具体计算步骤如下:
(1)在区间 [ a , b ] [a,b] [a,b]上, h = ( b − a ) h=(b-a) h=(b−a),计算分点的函数值 f ( a ) f(a) f(a)和 f ( b ) f(b) f(b)后,用梯形求积公式计算 T 1 T_1 T1:
T 1 = b − a 2 [ f ( a ) + f ( b ) ] T_1=\frac{b-a}{2}[f(a)+f(b)] T1=2b−a[f(a)+f(b)]
(2)将区间 [ a , b ] [a,b] [a,b]二分, h = ( b − a ) / 2 h=(b-a)/2 h=(b−a)/2,计算新增分点的函数值 f ( a + b 2 ) f(\frac{a+b}{2}) f(2a+b)后,用 T 2 n = 1 2 T n + 1 2 H ∑ k = 0 n − 1 f ( x k + 1 2 ) T_{2n}=\frac{1}{2}T_n+\frac{1}{2}H\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}}) T2n=21Tn+21H∑k=0n−1f(xk+21)计算 T 2 T_2 T2:
T 2 = 1 2 T 1 + h ∑ k = 0 n − 1 f ( x k + 1 2 ) T_2=\frac{1}{2}T_1+h\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}}) T2=21T1+hk=0∑n−1f(xk+21)
用 S n = 4 3 T 2 n − 1 3 T n S_n=\frac{4}{3}T_{2n}-\frac{1}{3}T_n Sn=34T2n−31Tn计算 S 1 S_1 S1:
S 1 = 4 3 T 2 − 1 3 T 1 S_1=\frac{4}{3}T_2-\frac{1}{3}T_1 S1=34T2−31T1
(3)将区间 [ a , b ] [a,b] [a,b]再二分, h = ( b − a ) / 4 h=(b-a)/4 h=(b−a)/4,计算新增分点 f ( a + a + b 4 ) f(a+\frac{a+b}{4}) f(a+4a+b)和 f ( a + 3 4 ( a + b ) ) f(a+\frac{3}{4}(a+b)) f(a+43(a+b))后,用 T 2 n = 1 2 T n + 1 2 H ∑ k = 0 n − 1 f ( x k + 1 2 ) T_{2n}=\frac{1}{2}T_n+\frac{1}{2}H\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}}) T2n=21Tn+21H∑k=0n−1f(xk+21)式计算 T 4 T_4 T4,用 S n = 4 3 T 2 n − 1 3 T n S_n=\frac{4}{3}T_{2n}-\frac{1}{3}T_n Sn=34T2n−31Tn计算 S 2 S_2 S2,用 C n = 16 15 S 2 n − 1 15 S n C_n=\frac{16}{15}S_{2n}-\frac{1}{15}S_n Cn=1516S2n−151Sn计算 C 1 C_1 C1:
C 1 = 16 15 S 2 − 1 15 S 1 C_1=\frac{16}{15}S_2-\frac{1}{15}S_1 C1=1516S2−151S1
(4)将区间 [ a , b ] [a,b] [a,b]再二分, h = ( b − a ) / 8 h=(b-a)/8 h=(b−a)/8,计算新增分点的函数值后,用 T 2 n = 1 2 T n + 1 2 H ∑ k = 0 n − 1 f ( x k + 1 2 ) T_{2n}=\frac{1}{2}T_n+\frac{1}{2}H\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}}) T2n=21Tn+21H∑k=0n−1f(xk+21)计算 T 8 T_8 T8,用 S n = 4 3 T 2 n − 1 3 T n S_n=\frac{4}{3}T_{2n}-\frac{1}{3}T_n Sn=34T2n−31Tn计算 S 4 S_4 S4,用 C n = 16 15 S 2 n − 1 15 S n C_n=\frac{16}{15}S_{2n}-\frac{1}{15}S_n Cn=1516S2n−151Sn计算 C 2 C_2 C2,用$R_n=\frac{64}{63}C_{2n}-\frac{1}{63}C_n 计 算 计算 计算R_1$:
R 1 = 64 63 C 2 − 1 63 C 1 R_1=\frac{64}{63}C_2-\frac{1}{63}C_1 R1=6364C2−631C1
(5)将区间 [ a , b ] [a,b] [a,b]再二分, h = ( b − a ) / 16 h=(b-a)/16 h=(b−a)/16,计算新增分点的函数值后,计算 T 16 , S 8 , C 4 , R 2 T_{16},S_8,C_4,R_2 T16,S8,C4,R2。
(6)将区间 [ a , b ] [a,b] [a,b]继续二分下去,可得Romberg序列 R 1 , R 2 , R 4 , ⋯ , R n , R 2 n R_1,R_2,R_4,\cdots,R_n,R_{2n} R1,R2,R4,⋯,Rn,R2n直至满足精度要求 ∣ R 2 n − R n ∣ ≤ ϵ |R_{2n}-R_n|\leq \epsilon ∣R2n−Rn∣≤ϵ为止。
由于加速过程中不需要再计算函数值,所以加速过程的计算量非常小,可以忽略不计,而加速效果则是十分显著的。