数据结构之线性表(三)——顺序存储结构(3 顺序表基本操作的实现)
知识准备
-
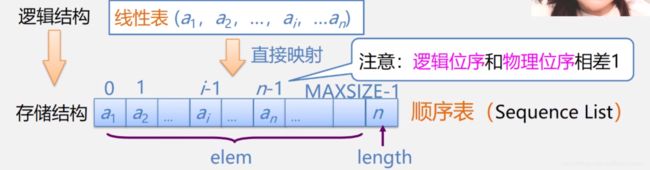
顺序表到底是怎么存储的?
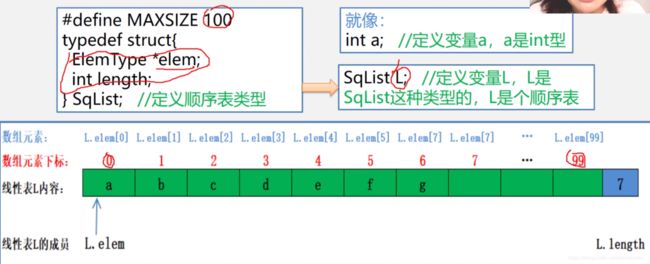
只有执行SqList L操作时,计算机才会分配内存,若只执行SqList,则计算机不会分配内存。
SqList L:指定义了一个SqList类型的变量L,这里L是顺序表,SqList是顺序表L的类型名。
从L中取成员:
若L为指针,即,SqList* L,取成员表示为,L->elem; L->length若L不是指针,即,SqList L,取成员表示为,
L.elem; L.length -
预定义常量和类型
- 预定义常量
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
- 预定义类型
typedef int Status;
typedef char ElemType;
顺序表的各种基本操作
1. 线性表L的初始化(传入参数为引用)
Status InitList_Sq(SqList& L) //构造一个顺序表L
{
L.elem = new ElemType[MAXSIZE]; //为顺序表L分配内存空间
if (!L.elem) //存储分配失败,抛出异常
exit(OVERFLOW);
L.length = 0; //空表长度为0
return OK;
}
2. 销毁线性表L
void DestroyList(SqList& L)
{
if (L.elem)
delete L.elem; //释放存储空间
}
3. 清空线性表L
void ClearList(SqList& L)
{
L.length = 0; //将线性表的长度设置为0
}
4. 求线性表L的长度
void GetLength(SqList L)
{
return L.length;
}
5. 判断线性表L是否为空
int IsEmpty(SqList L)
{
if (L.length == 0)
return 1;
else
return 0;
}
6. 顺序表的取值(根据位置i获取相应位置数据元素的内容)
int GetElem(SqList L, int i, ElemType& e)
{
if (i<1 || i>L.length) //判断i值是否合理,若不合理,返回ERROR
return ERROR;
e = L.elem[i - 1]; //第i-1个单元存储第i个数据
return OK;
}
以上算法复杂度为 O ( 1 ) O(1) O(1),这就体现了顺序表的优点,即可以随机存取(可以通过下标取到任意一个元素)。
7. 顺序表的查找(按值查找,顺序查找法)
- 在线性表L中找到与指定值e相同的数据元素的位置。
- 从表的一端开始,逐个与给定值进行比较,找到,返回该元素的位置序号,未找到,返回0。
int LocateElem(SqList L, ElemTye e)
{
for (i = 0, i < L.length, i++)
{
if (L.elem[i] == e)
return i + 1; //查找成功,返回序号
return 0; //查找失败,返回0
}
}
时间复杂度:
该算法的复杂度取决于指定值e在顺序表中的位置,所以,这里用平均查找长度 ASL(Average Search Length)表示其复杂度。
对于有n个记录的表,查找成功时,其ASL计算公式为,
A S L = ∑ i = 0 n P i C i ASL=\sum_{i=0}^nP_iC_i ASL=i=0∑nPiCi
P i P_i Pi:第i个记录被查找到的概率
C i C_i Ci:找到第i个记录需要比较的的次数
即,求取期望的公式。
所以,上述顺序查找法的ASL为,
A S L S S = ∑ i = 0 n P i C i = 1 n ∑ i = 0 n i = 1 n ∗ n ( n + 1 ) 2 = n + 1 2 ASL_{SS}=\sum_{i=0}^nP_iC_i=\frac{1}{n}\sum_{i=0}^ni=\frac{1}{n}*\frac{n(n+1)}{2}=\frac{n+1}{2} ASLSS=i=0∑nPiCi=n1i=0∑ni=n1∗2n(n+1)=2n+1
所以,该算法的复杂度为 O ( n ) O(n) O(n)。
8. 顺序表的插入算法
顺序表中可以插入元素位置为,
1 ≤ i ≤ n + 1 ( n 为 表 的 长 度 ) 1\le i\le n+1(n为表的长度) 1≤i≤n+1(n为表的长度)
其不同插入位置的算法演示,
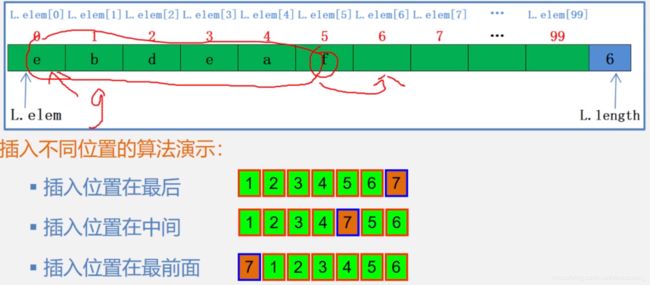
算法思想:
- 判断插入位置i是否合法,即 1 ≤ i ≤ n + 1 1\le i\le n+1 1≤i≤n+1。
- 判断顺序表的存储空间是否已满,若已满则返回ERROR。
- 将第n至第i位的元素依次向后移动一个位置,空出第i个位置。
- 将要插入的新元素e放入第i个位置。
- 表长加1,插入成功返回OK。
Status ListInsert_Sq(SqList& L, int i, ElemType e)
{
if (i<1 || i>L.length + 1)
return ERROR; //i值不合法
if (L.length == MAXSIZE)
return ERROR; //当前存储空间已满
for (j = L.lenth - 1; j >= i - 1; j--)
L.elem[j + 1] = L.elem[j]; //插入位置及之后的元素后移
L.elem[i - 1] = e; //将新元素e放入第i个位置
L.length++; //表长增1
return OK;
}
时间复杂度:
该算法时间主要耗费在移动元素的操作上,
- 若插入在尾结点之后,则无需移动(特别快);
- 若插入在首结点之前,则表中元素全部后移(特别慢);
- 若在第i个位置插入一个元素,则其ASL为,
A S L = ∑ i = 0 n P i C i = 1 n + 1 ∑ i = 0 n ( n − i + 1 ) = 1 n + 1 ∗ n ( n + 1 ) 2 = n 2 ASL=\sum_{i=0}^nP_iC_i=\frac{1}{n+1}\sum_{i=0}^n(n-i+1)=\frac{1}{n+1}*\frac{n(n+1)}{2}=\frac{n}{2} ASL=i=0∑nPiCi=n+11i=0∑n(n−i+1)=n+11∗2n(n+1)=2n
所以,该算法的平均时间复杂度为 O ( n ) O(n) O(n)。
9. 顺序表的删除算法
顺序表中可以插入元素位置为,
1 ≤ i ≤ n ( n 为 表 的 长 度 ) 1\le i\le n(n为表的长度) 1≤i≤n(n为表的长度)
删除算法演示,
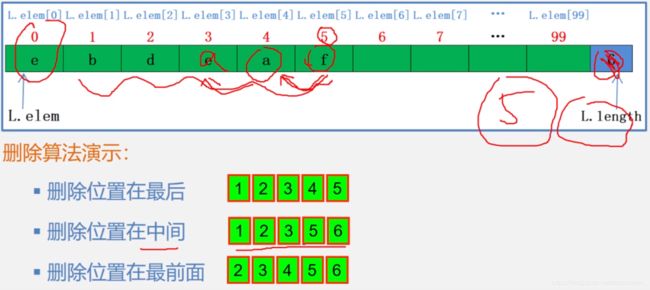
算法思想:
- 判断删除位置i是否合法,即 1 ≤ i ≤ n 1\le i\le n 1≤i≤n。
- 将欲删除的元素保留在e中。
- 将第i+1至第n位的元素依次向前移动一个位置。
- 表长减1,删除成功返回OK。
Status ListDelete_Sq(SqList& L, int i)
{
if (i<1 || i>L.length)
return ERROR; //i值不合法
for (j = i; j <=L.length-1; j++)
L.elem[j - 1] = L.elem[j]; //被删除元素之后的元素前移
L.length--; //表长减1
return OK;
}
时间复杂度:
该算法时间主要耗费在移动元素的操作上,
- 若删除尾结点,则无需移动(特别快);
- 若删除首结点,则表中n-1个元素全部前移(特别慢);
- 若在第i个位置删除一个元素,则其ASL为,
A S L = ∑ i = 0 n P i C i = 1 n ∑ i = 0 n ( n − i ) = 1 n ∗ n ( n − 1 ) 2 = n − 1 2 ASL=\sum_{i=0}^nP_iC_i=\frac{1}{n}\sum_{i=0}^n(n-i)=\frac{1}{n}*\frac{n(n-1)}{2}=\frac{n-1}{2} ASL=i=0∑nPiCi=n1i=0∑n(n−i)=n1∗2n(n−1)=2n−1
所以,该算法的平均时间复杂度为 O ( n ) O(n) O(n)。