数值优化（Numerical Optimization）学习系列-线搜索方法（LineSearch）

概述

在求解最优化问题中，线搜索是一类非常重要的迭代算法。线搜索的迭代过程是 xk+1=xk+αkpk 。其中 αk 和 pk 分别表示搜索步长和搜索方向，因此线搜索需要解决如何求解步长和确定搜索方向，该小结主要介绍
1. 步长 αk 的选择
2. 步长的实现算法
2. 线搜索的收敛性
3. 牛顿方法的优化

步长 α 的选择

根据迭代算法 xk+1=xk+αkpk ，根据之前的介绍搜索方向 pk 需要满足，它是一个下降方向，即满足 ∇fkpk≤0 ，则 pk=−B−1k∇fk ，B为对称非奇异矩阵，根据 Bk 的选择会产生以下几个方向:
1. Bk=I 时，搜索方向为负梯度方向，该方法为最速下降方向。
2. Bk=∇2fk 时，该方法为牛顿方法。
3. Bk 需要满足对称正定矩阵，该方法为拟牛顿方法。
当搜索方向确定后，下一步就要确定步长。

问题形式

求解步长需要解决的一个最优化问题是，在确定了下降方向 pk 后，求解一个一元最优化问题

minϕ(α)=f(xk+αpk)

.

精确算法

对于一个一元二次问题，最优解形式为 ∇Tf(xk+αpk)pk=0 ，即 ∇Tfk+1pk=0

性质：对于最速下降法，当选择最优步长时，每一步的搜索方向和上一步是正交的，即 pTk+1pk=0

证明：由于当选择为最优步长时满足 ∇Tfk+1pk=0 。因此性质成立， pk+1=−∇fTk+1

非精确算法

非精确算法的思路就是寻找步长 α 的一个区间，通过逐步二分的方法去寻找满足条件的点。当搜索结束时，需要满足该步长能够对目标函数带来充分的减少。为提高非精确算法的搜索效率， α 需要满足一定的条件。

Armijo条件

Armijo是一个相对比较简单的条件，即目标函数需要充分小。

f(xk+αpk)≤f(xk)+c1α∇fTkpk,c1∈(0,1)

通常情况下记：

ϕ(α)=f(xk+αpk)

表示原始最优化目标函数。

l(α)=f(xk)+c1α∇fTkpk

表示退化后的目标函数。
在实际应用中， c1 选择为10^-4，满足Armijo条件的情况如下图所示

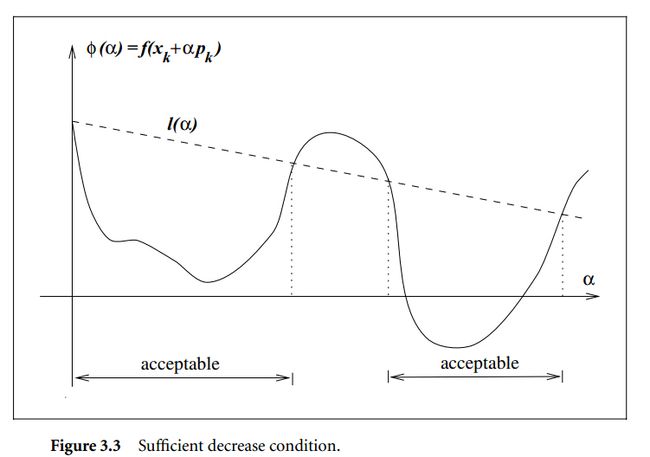
Curvature条件

Curvature条件是指：

∇f(xk+αkpk)Tpk≥c2∇fTkpk,c2∈(c1,1)

其中c1就是Armijo中的c1.
Curvature条件中的左边就是 ϕ′(αk) ，而右边是 ϕ′(0) ，或者 l′(α) ，即在第K点的曲率要比初始点的曲率要大。由于右边是负值，则左边就是一个接近0或者大于0的一个值。
直观上看，如果该值接近0时，曲率接近水平，这样就接近最优解。图示如下

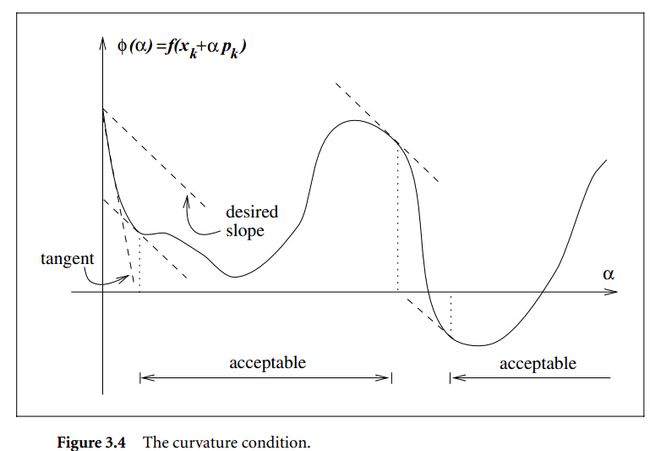
Wolfe条件

把上面两个条件组合后就是Wolfe条件，即需要满足

f(xk+αpk)≤f(xk)+c1α∇fTkpk∇f(xk+αkpk)Tpk≥c2∇fTkpk0<c1<c2<1

如果进一步进行约束， 强Wolfe条件需要满足

f(xk+αpk)≤f(xk)+c1α∇fTkpk|∇f(xk+αkpk)Tpk|≤c2|∇fTkpk|0<c1<c2<1

强Wolfe条件对正负曲率都进行了约束，条件更强。
满足Wolfe条件的区间如下图
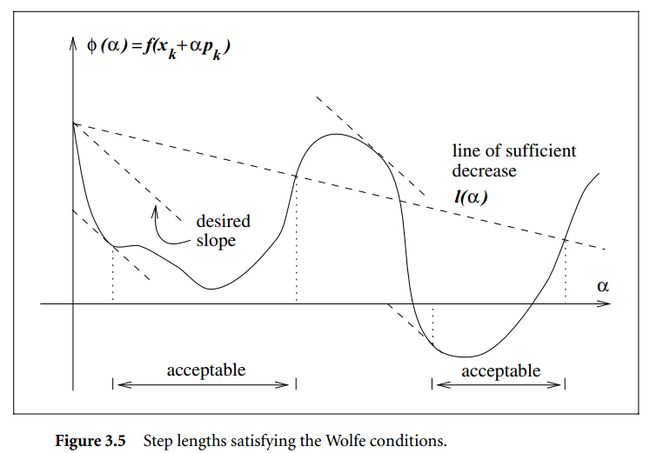
满足强Wolfe条件的区间如下图

Wolfe条件存在性证明

定理:假设目标函数f是一个连续可导的，并且搜索方向 pk 为下降方向，同时函数f是有界的，在射线 xk+αpk 之下，则如果 0<c1<c2<1 ，存在步长 α 满足Wolfe条件和强Wolfe条件。

证明：由于f在被限定在射线 xk+αpk 之下，则函数 ϕ(α)=f(xk+αpk) 和函数 l(α)=fk+αc1∇fTkpk 存在交点。
1. 记最小的交点为 α′ ，则小于 α′ 的区间都满足Wolfe的第一个条件。交点满足

f(xk+α′)=f(xk)+α′c1∇fTkpk

2. 随机选择 α′′∈(0,α′) ，根据中值定理有

f(xk+α′)−f(xk)=α′∇f(xk+α′′pk)Tpk

3. 根据上面两个等式有

c1∇fTkpk=∇f(xk+α′′pk)Tpk≤c2∇fTkpk

此时 α′′ 满足Wolfe的第二个条件

Goldstein条件

该条件类似于Wolfe条件，但是需要步长减少的不能太少。该条件为

fk+(1−c)αk∇fTkpk≤f(xk+αkpk)≠fk+(c)αk∇fTkpk

参数 c∈(0,0.5)
满足该条件的步长被两个射线包围着，使用该方法可能会错过最优解，图示如下

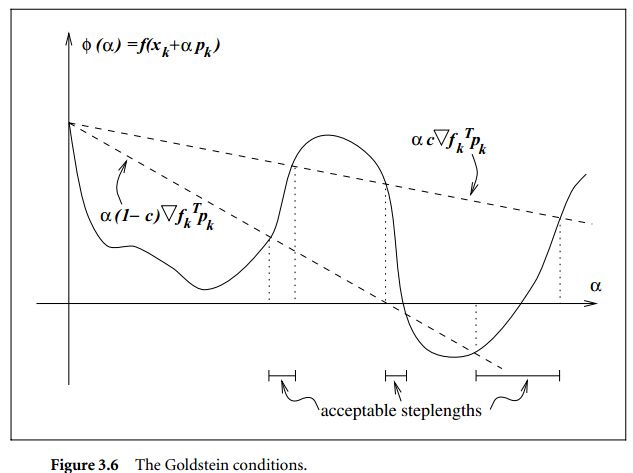
步长 α 求解算法

根据上面的介绍，我们可以知道求解步长，需要解决的问题是

αk=arg minϕ(α)=arg minf(xk+αpk)

分两类问题进行讨论：
1. 如果目标函数是凸函数，并且 f(x)=12xTQx−bTx ，则步长的最优解为 α=−∇fTkpkpTkQpk
2. 如果目标函数是一个非线性问题，就需要用到迭代算法求解，寻找最优步长或者满足上述必要条件的步长。本节主要讨论 目标函数的梯度存在，如果不存在还会有其他算法。求解步骤一般分为两步，一是寻找一个包含解的区间，二是逐渐放大该步长，直到满足条件。

插值法

使用插值法的目标是寻找一个步长的递减序列，直到找到一个满足约束的步长。

二次插值

根据Armijo条件，步长的选择应该满足使得目标函数充分减小，该条件为

f(xk+αpk)≤f(xk)+c1α∇fTkpk

对于第K步的 α 应该满足：

ϕ(αk)≤ϕ(0)+c1αkϕ′(0)

对于初始值 α0 满足上述约束，则结束。否则减小步长值，即 α1∈(0,α0) 。
此时运用二次插值法，寻找插值函数 ϕq(α) 满足一下条件

ϕq(0)=ϕ(0),ϕ′q(0)=ϕ′(0),ϕq(α0)=ϕ(α0)

，根据上述条件，求得 ϕq(α) 为：

ϕq(α)=(ϕ(α0)−ϕ(0)−α0ϕ′(0)α20)α2+ϕ′(0)α+ϕ(0)

求解该一元二次最优化问题可以得到

α1=ϕ′(0)α202(ϕ(α0)−ϕ(0)−α0ϕ′(0))

三次插值

如果上述\alpha_1满足约束条件则结束，否则需要进行三次插值，即寻找插值函数 ϕc(α) 满足一下值相等， ϕ(0),ϕ′(0),ϕ(α0),ϕ(α1) 。假设求得 ϕc(α) 为

ϕc(α)=aα3+bα2+aϕ′(0)+ϕ(0)

可以根据代入法求解参数值，此时下一个步长 α2 为

α2=−b+b2−3aϕ′(0)−−−−−−−−−−√3a

如果满足约束则结束，否则继续利用最近的两个步长值和初始值继续进行三次插值，直到结束。如果两次的步长比较相近，则 αk=αk−12

初始化步长选择

对于牛顿或者拟牛顿法，初始化步长可以选择为1，对于其他非scaled的方法，初始化比较重要。
1. 方法一假设在 xk和xk−1 处一阶梯度改变相同，即满足 α0∇fTkpk=αk−1∇fTk−1pk−1
2. 在 f(xk−1),f(xk),∇fTk−1pk−1 处进行二次插值，此时 α0=2(fk−fk−1)ϕ′(0)

步长求解算法

寻找满足强Wolfe条件的步长，该条件为

f(xk+αpk)≤f(xk)+c1α∇fTkpk|∇f(xk+αkpk)Tpk|≤c2|∇fTkpk|0<c1<c2<1

该算法分为两步，一是寻找一个包含解的区间；二是运用zoom算法寻找满足约束条件的解。

算法框架

在调用zoom算法前，寻找一个步长的下界使得在该区间内包含最优解 α∗ ，算法描述如下
算法主要包含以下4步
1. 评价当前步长，判断是否满足充分小条件，如果不满足说明最优解在 (αi−1,αi) 之间。
2. 否则满足强Wolfe的条件1，验证条件2是否满足，如果满足则结束。
3. 如果不满足条件2，并且当前梯度为正值时，交互上一个步长调用zoom算法结束（为什么调换，看zoom算法介绍）
4. 求解下一个步长点，可以采用插值法。
下图描述了需要调用zoom算法的两类条件，分别对应1和3：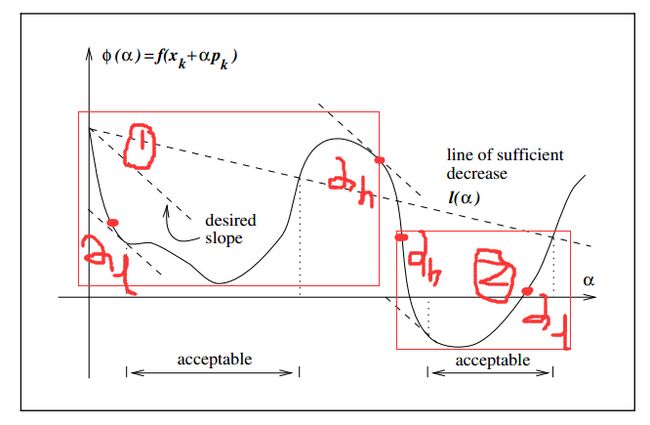

zoom算法

zoom算法的输入比较特殊，输入需要满足 (αl,αh)
1. 该区间内包含满足强Wolfe条件的步长
2. 步长 αl 是两个值中目标函数值较小的一个
3. 选择 αh 如果该点满足 ϕ′(αl)(αh−αl)<0，表明该区间是一个连续下降的区间
zoom算法描述如下
算法流程为
1. 检查是否满足Wolfe的条件一，如果不满足缩减区间。
2. 检查是否满足条件2 ，如果满足则返回
3. 检查是否是递增区间，如果是进行调整，使其满足zoom输入条件。

线搜索的收敛性

1. 如果搜索方向选择为“最速下降方向”即负梯度方向，则能达到一个“全局收敛”状态，此时满足 limk→∞||∇fk||=0
2. 对于牛顿方法或者伪牛顿方法 (pNk=−B−1k∇fk) 只要满足Bk的条件数有界限并且正定则也能达到全局收敛。
3. 对于共轭梯度方法，只要满足 limk→∞inf||∇fk||=0 ，即只要一个子序列收敛即可。
4. 对于任何搜索方向，只要满足1）每一个步目标值都在下降2）每隔一定步数都能达到一个最优下降方向，都能收敛。即不要求每一步都下降，可以周期性下降。

收敛速度

1. 当搜索方向为最优下降方向是，为线性收敛速度。

2. 当搜索方向为牛顿方向，即 pNk=−∇2f−1k∇fk ，如果 ∇2fk 正定，则牛顿法为二次收敛。（但是牛顿方向不总是为正定，因此Hessian在使用时需要进一步调整）

3. 当搜索方向为伪牛顿方向时，收敛速度为超线性。

牛顿方法–Hessian矩阵替代品

1. 牛顿方法中，搜索方向需要满足 ∇2fkpNk=−∇fk ，如果 ∇2fk 正定，可以得到搜索方向

2. 牛顿方法中，Hessian矩阵不总是正定的，会导致搜索方向不总是下降方向，从而导致牛顿方法不总能找到最优解。

3. 但是可以找到一些替代方法，例如

   • 通过特征值修改： ∇2fk=QΛQ
   • 添加常数因子，$B_k=\nabla^2f_k+λI\$
   • 修改Cholesky算法

总结

通过该章的学习，能够了解
1. 线搜索的基本形式以及需要解决的问题
2. 常见步长 α 需要满足的条件以及实现算法
3. 线搜索的收敛速度
4. 牛顿方法的优化