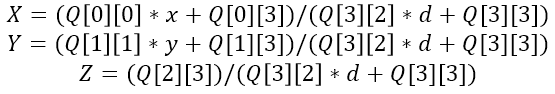基于格雷码+相移方案的结构光重建解析
由于前段时间一直处在算法的应用开发阶段，长时间将心思花在硬件选型、原型机设计、原型机搭建和联调等上面，没有抽足够的时间来记录相关算法的开发经历，年底特更新一篇有关格雷码+相移方案的三维重建算法，该文章依据相应论文，对格雷码+相移方案的整个重建进行了较为详细的阐述，并融入了自己对该套方案的看法，便于广大的同仁一起研讨，文章中如有不妥之处，也请指正。
整个文章将以双目结构光为基础，内容包括以下几个部分：
0.格雷码+相移基本原理；
1.双目相机的标定；
2.图像校正；
3.图像解码；
4.图像解包；
5.匹配点计算；
6.三角计算；
7.该方案相关问题分析。
其中，针对 格雷码+相移基本原理 做详细介绍。
注意，双目的格雷码+相移方案中囊括不同的类型，例如，水平和垂直投影的双路格雷码+相移方案，仅水平投影或者垂直投影的格雷码+相移方案。不同的类型，在匹配点计算和三角计算方案稍有不同，但是万变不离其宗，都是得到唯一确定的绝对相位，并依据匹配法则，建立匹配点对，最后计算空间三维点坐标。该文章讨论垂直投影（条纹光栅垂直）的双目格雷码+相移方案。
-------------------------------------------------------
0.格雷码+相移基本原理
格雷码+相移方案是结合了传统格雷码方案和光栅相移方案，将解码和解包统一成解包（解绝对相位）。其中，格雷码条纹主要是确定主相位，相移光栅主要是确定包裹相位，最后将二者组合在一起就完成了整个相位解包（全局绝对相位）。
该方案的一个关键问题是如何确定格雷码位数和相移的周期。一般地，先确定正整数级的格雷码位数，然后结合pattern的大小，确定相移周期的大小，至于为啥要这样操作，下面将进行详细阐述。
在阐述之前，先说一下传统的格雷码方案（该方案简洁、直观，便于理解），若投影仪的分辨率是1024*768，那么如要对投影仪每个像素点镜唯一编码，需要1024个不同的编码值，10bit的编码刚好是pow(2,10)=1024，这样每个像素点的编码值确定后，就可以直接进行后续的匹配计算，但是10bit的格雷码需要10张的pattern，高频pattern中编码条纹极细，相机在捕获投射的条纹时，极易受噪声影响，后续解码极易出现解码错误，影响最终的重建效果！
格雷码+相移的方案，在纯格雷码的基础上，摒弃了高频的pattern，取而代之的是浮点型的相移pattern，这样做一方面，提高了pattern捕获的稳定性，另外在一定程度上减少了pattern张数。
当然，格雷码+相移的解相位（格雷码解码值可以通过*2PI转化成相位值）跟纯格雷码解码值是一样的，也需要确定唯一性！这样，如何让该套方案能够完成唯一性咧？这是该方案设计的核心点！通常来讲，摒弃高频段的格雷码是无法完成整个图像的唯一编解码的，这样就需要用到相移法。另外可知，相移pattern是周期性的，单频的解相位，解出的相位是包裹相位（也是周期性），也无法得到唯一解相位。但是，将两者合理地结合在一起，就可以完美地解决唯一性问题。
例如，投影仪的分辨率是1024*768，编码数量需要不少于1024，如采用6格雷码+4相移方案（pattern如下图，pattern是1140*912大小）。格雷码部分，pow(2,6)=64，这样，仅通过格雷码解码可以确定64个不同的编码区域（0~63），远远不能满足1024个解码问题！推想之，如能在格雷码的不同区域内再细分编码，那么就可以得到不同的编码值。当然，编码值都是整数，无法再进行细分！但是，可以将整数范围统一到浮点范围，刚好相位法的解包是浮点型！现在问题已经非常明朗了，如何桥接格雷码和相移成了下一步的关键。
以下是格雷码端pattern
以下是相移端pattern
通过对相移法的学习（如不清楚，可先学习相关内容，此处不做介绍）可知，解相位的范围是-PI~PI，周期是2PI。这样，对格雷码解码区放大2PI，再加上相移的解相位值，即 N*2PI+(-PI~PI)，其中N=0,1,2,...,63，就可以顺利完成相位唯一性问题了！接下来就是相移参数（相移周期）的确定。
已经确定了格雷码+相移是可行的，且确定了格雷码的位数（该处选取格雷码位数是6，当然可取其它值）。相移的周期只需要在不少于一个格雷码区域内满足唯一性就行，如刚好在一个周期内，那么相移的周期T就是格雷码一个编码区域内的像素数量。还是针对上述说的1024*768的分辨率，如采用 6格雷码+4相移的方案，格雷码的编码区域数量是pow(2,6)=64，那么每个区域内像素数量就是num=1024/64=16，也就是相移周期T>=16就行，这样就可以设计好相移参数。为何这样就可以完成唯一性问题咧？请看以下图表：
第一行是格雷码在相位范畴的数值，第2到4行分别是T
到此，完成了相位唯一性问题！但是还有个小问题需要说明，通过上述的方法，投影垂直条纹仅仅确定了水平走向的相位唯一性，可是每列的解相位值却都是一样的，没有完成唯一性！针对这个问题，有两种解决方案，一种是再追加投影水平条纹，解决垂直走向的相位唯一性问题，这样通过交叉定位，就可以完美解决整图的位置；另一种是结合对极几何极线约束，对图像进行校正，达到行对齐，这样后面仅通过行内匹配就可以确定位置了！该文章所阐述的是采用第二种方案，仅投影一路，后续对图像进行校正。
-------------------------------------------------------
1.双目相机的标定
双目相机的标定十分简单，通过投射不同方位的图片，解算两个相机之间的相对位置关系，以及各自的内部参数。在这里，特别要注意的是，在立体标定完成后，需要对图像进行校正，得到校正后的投影矩阵和深度映射矩阵，便于在应用端对采集的目标图像进行校正操作。
标定对后面的三维重建至关重要！在标定前，要确定好相机镜头的畸变类型，一般普通的镜头都是以径向畸变为主，最好不要忽视切向畸变，为此镜头畸变参数可确定为k1 k2 p1 p2 k3，k1 k2 k3表示径向畸变系数，p1 p2表示切向畸变系数（镜头畸变补偿公式请参见相关文献，此处不做介绍）。此外，为了提高标定精度，一般需要从多个视角位置捕获标靶图像（有关论文验证，摆放次数在10~20次为宜），且最好让标靶上特征能够布局在整个视场范围。一个不成文的规定，一般标定的重投影在0.1pixel以下表示标定精度尚可，若标定的重投影过大，请检查标定模型，标靶布局，以及标靶精度等。
-------------------------------------------------------
2.图像校正
针对一路投影方式，由于无法确定另一个方向的解相位情况，所以需要对图像进行校正，以便达到行对齐。
图像的校正严格来说，分为两个方面：一个是畸变的矫正，另一个是图像方位的校正。校正后的图像光轴是平行的，如下图所示：
图像校正可以按照以下流程：
a.根据相机的内外参数，建立校正查找映射表LUT；
b.利用LUT，对原始的图像进行校正（里面涉及到插值）。
上述流程涉及到了两大内容：共面和行对齐。
共面是实现图像平面处在一个平面内（此时未能行对齐），具体做法是将相机旋转矩阵R划分为左右相机的合成矩阵
、
；行对齐是建立对准矩阵
将图像极点转化到无穷远处，以便达到行对齐。具体公式如下：
![r_{l}=R^{1/2},r_{r}=R^{-1/2},R_{rect}=[e_{1}\, e_{2}\: e_{3}]^{T}](http://img.e-com-net.com/image/info8/76ef3116e99a4c15a0f1fef00f03f994.gif){kind=small}
，其中
是与平移向量T同方向的极点，![T=[T_{x}\,T_{y}\,T_{z}]^{T}](http://img.e-com-net.com/image/info8/252bc07f56ec4c3e957aa9aa9304f8db.gif){kind=small}
；![e_{2}=[-T_{y}\, T_{x}\,0]^{T}/\sqrt{T^{2}_{x}+T^{2}_{y}}](http://img.e-com-net.com/image/info8/6b407868c2c449f890c75cceae159836.gif){kind=small}
为图像平面方向的向量；
是垂直于
与
所在平面的向量。
左右相机的行对准转换矩阵
，
。
图像校正后，后续的图像匹配点搜索就可以限制在一维行内进行，大大提高了匹配效率。
后续提高的图像操作，均是校正后的图像。
-------------------------------------------------------
3.图像解码
这个提到的解码指的是格雷码的解码，无论是多少位的格雷码，采用异或的方式对所有相邻格雷码图像进行处理，最后将所有的异或结果扩大相应的2的位数幂次方后求和得到一个总体的解码值。
这里需要注意的是首先要对图像进行二值化，二值化的阈值可根据实际情况选定（该阈值不十分敏感，对于灰度图一般取100即可）。例如，6格雷码中对应位置的二值化结果是 0 1 1 1 0 0，异或后的结果为0 1 0 0 1 0，最后的解码值应该是 0*32+1*16+1*8+1*4+0*2+0*1=28，该值亦是解码区域的编号（0 1 2 ... 63），后续结合相移结果得到解包相位时，需要对此值扩大2PI（转化到相位弧度范畴）。当然这里的解码方式并不是唯一的，只要可以区分不同编码区域即可。
-------------------------------------------------------
4.图像解包
图像解包主要有两个步骤：首先是相移图像的包裹相位计算，针对4相移方式，包裹相位计算公式为：
，该公式的计算结果在-PI~PI范围内，当然可以加上PI，转化至0~2PI范围；然后加上图像解码中得到的相位值（解码值扩大2PI）。例如，某处解码值是2，包裹相位是PI/3，那么该处最终的解包相位是2*2PI+PI/3。
这样，就完成了整个图像的解相位操作，可以从解包相位图上看出，每一行中不同位置的相位值均不相同（理论情况下），后续的对应点匹配搜索将以相位值为基础进行。
-------------------------------------------------------
5.匹配点计算
得到全局解包相位后，就可以行遍历，搜索匹配满足阈值的匹配点。相位匹配搜索所用到的阈值对匹配效果较为敏感！在实际操作过程中，最好通过多组实验确定不同测量距离，不同相机分辨率下该阈值的大小。一般地，如果得到的匹配点对极少，可适当增大阈值，如果得到的匹配点对非常多，且匹配效果极差，可适当减小阈值。
匹配点计算部分比较耗时，可以考虑使用较为高效的匹配算法，并进行高并行计算。
-------------------------------------------------------
6.三角计算
三角计算即根据匹配点对，以及相机的位置关系等反向求解同名点（匹配点对）在空间中的位置坐标。针对校正后图像的三角计算，可以根据视差计算，因为校正后图像的行是对齐的，图像在垂直方向上没有视差，仅仅只有水平方向的位置移动。
以下提供两种方式进行三角计算，一种是根据左右相机的投影矩阵，另一种是根据左右相机之间的深度映射矩阵。
根据左右相机的投影矩阵进行计算过程稍微复杂，其主要流程如下：
a.利用匹配点和投影矩阵，计算4*4的中间方阵A（如下图）；
b.利用SVD对中间方阵A进行奇异值分解；
c.奇异值分解后的V向量的最后一行即为4维的空间点齐次坐标；
d.对4维齐次坐标进行归一化处理，得到最终的3维空间点坐标。
对于通过上述操作为何就可以得到三维点空间坐标，可自行查询相关的文献资料，此处不做介绍。
其中，
是相机的投影矩阵，
是一对匹配点。
SVD分解：
，V即为4维齐次坐标，最终的三维坐标即为：![[X \,Y \,Z]=[V_{3,0}/V_{3,3}\,V_{3,1}/V_{3,3}\,V_{3,2}/V_{3,3}]](http://img.e-com-net.com/image/info8/85fe492330df44d18e8d764e5b43fcf1.gif){kind=small}
根据左右相机之间的深度映射矩阵来计算三维点较为简单，例如在标定过程中立体校正得到的映射矩阵为Q，那么其主要计算过程如下：
对此，整个重建计算完成，当然，也可以根据匹配点位置，为每个三维点添加纹理信息（需要彩色相机）。
-------------------------------------------------------
7.该方案相关问题分析
从上述描述可以看出，基于格雷码+相移方案的结构光三维重建过程并不难，但是，想要得到高精度、高稳定性、高效率的三维重建效果，优化的地方还是很多，需要花费不少的功夫！
通过对该套方案的解读，不难看出该方案的重建仍然是建立在像素级上的！因为匹配点对始终是像素级的匹配，在一定程度上提高相机的分辨率可以提高重建精度，但是过分提高相机分辨率会导致相位过于细化，这样，当整个系统的噪声较大时，细化的相位会与噪声交织在一起，大大降低重建效果！
另外，该方案仍然是基于立体匹配的三维重建方式，其中有关点对匹配计算和三角计算过程较为耗时，该方案很难做到实时处理！若想达到实时处理（每秒可以完成10个甚至更多场景的三维重建），一般要采用基于相位—高度映射的三维重建方式，目前较好的方式是单频3相移结构光方案，该方案仅需要投射3幅相移图像，然后利用相位—高度映射算法对解算的相位进行高度转化，同时结合标定参数，通过LUT计算不同位置的三维坐标。
-------------------------------------------------------