[论文阅读笔记---Few Shot 1]Siamese Network

背景

        小样本问题: 与大规模数据集下的分类问题考虑的角度不同，小样本学习考虑如何从少量的样本中学习，即当模型学习到一定类别的数据后，给定少量新类别的样本，模型也能较准确的识别出类型。

        one-shot learning: 数据集中每个类别仅仅有一个或几个样本。

图1 传统的分类问题

       

图2 小样本问题

Siamese Network

        通常的分类问题(如ImageNet)，数据集庞大，每一种类别的样本数目多，此时构建一个合适的分类器即可实现良好的效果。通长的做法是，网络结构可参考另一篇博客。从上图可以看出，测试集的样本类型在训练集中有出现。

       但某些实际应用中，用户数据集的种类多，但对应到每一种的样本很少，可能只有几十个甚至几个，若按照之前的做法，可能会出现过拟合，此时需要考虑Siamese网络这种相似性度量的方法，此时网络并不直接输出样本的类别，而是看做一个Similarity函数 ，输出两个128维度的向量。

图3 Siamese Network网络结构

        上图(来自deepAI)描述了Siamese 网络的基本结构，网络中输入两个样本，最终输出得到两个样本的特征向量。

• 如果两个样本属于同一个类别，则上下两个模型的向量之间的欧拉距离较小
• 如果两个样本属于不同类别，则上下两个模型的向量之间的欧拉距离较大

        最终对网络输出的两个向量，计算欧拉距离，得到的值作为两张图片的相似度。上述两个网络共享参数。

图4 Siamese网络结构

损失函数

Contrastive loss

        Contrastive Loss的输入也是两个成对的样本对，label为两个样本是否属于同一类，计算方法为

        其中,表示映射后的embedding向量，同一类的两个向量，欧拉距离不可能为0。当两个样本处于不同类时，m为预先设定的阈值，表示属于不同类的两个样本的距离应该大于m，上述式即保证处于同一类型的样本距离尽可能小，而处于不同类型的样本距离尽可能大。

Triplet Loss

        要训练上述网络，需要考虑cost function后，利用梯度下降法等优化算法寻找最优解。

        Siamese Network中使用的Loss Function为Triplet Loss，Triplet Loss也可看做比较两个向量相似性的一个较为有效的损失函数。

        Triplet是一个三元组，包括三个参数anchor, positive, negative，每一个参数都是一个embedding向量。anchor指的是基准图片，positive指的是与基准图片处于同一类的图片，negative表示与基准图片不是同一类的图片。

        在训练时，首先从训练集中选取一个样本作为Anchor，然后再随机选取一个与Anchor同类别的样本作为Positive，最后从其他样本中随机选取一个Negative。

        训练上述网络的目标是，，损失计算公式为

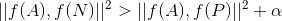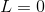• 当时，损失，此时模型对正负样本的差异较大
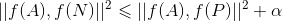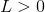• 当时，损失，此时模型对正负样本的差异较小

        相对于Contrastive Loss, Triplet Loss考虑了锚点与正负样本之间的距离关系。其中为阈值，可控制正负样本之间的距离，控制正负样本的距离之间有一个很小的间隔，越大，不同类别之间的差异越大，不同类别之间的可区分度越强。

学习策略：

simi-hard negative sample mining

• 特征提取
• 距离度量
• 相似性比较

参考资料

DeepFace: Closing the Gap to Human-Level Performance in Face Verification

FaceNet: A Unified Embedding for Face Recognition and Clustering

为什么triplet loss有效？

triplet loss原理推导及变体

Generalizing from a Few Examples: A Survey on Few-Shot Learning

https://github.com/harveyslash/Facial-Similarity-with-Siamese-Networks-in-Pytorch

https://github.com/brendenlake/omniglot

https://zhuanlan.zhihu.com/p/61215293

https://zhuanlan.zhihu.com/p/99116121