一步步地分析排序——归并排序
前言
本文是对《算法》第四版归并排序所做的笔记,归并排序之所以值得我们仔细学习,有几个原因:
- 归并排序是非常经典的基于分治法的递归排序算法。
- 和初级排序算法(冒泡、选择、插入)在最坏的情况下时间复杂度会达到O(N2)相比,归并排序在最坏的情况下仍有O(NlgN)的效率。
- 归并排序和另一个非常重要的排序方法:快速排序非常相似,都是基于分治法的递归排序,甚至于它们两者的过程近似于互补。如果你能很好地理解归并排序,会有助于以后快速排序的学习。
简单地介绍完了归并排序之后,来说一下本文脉络:
- 归并排序的概念
- 一次“归并”的过程
- 原地归并的抽象方法及其详解
- 自顶向下的归并排序及其详解、优化方案
- 自底向上的归并排序分析
归并排序的概念
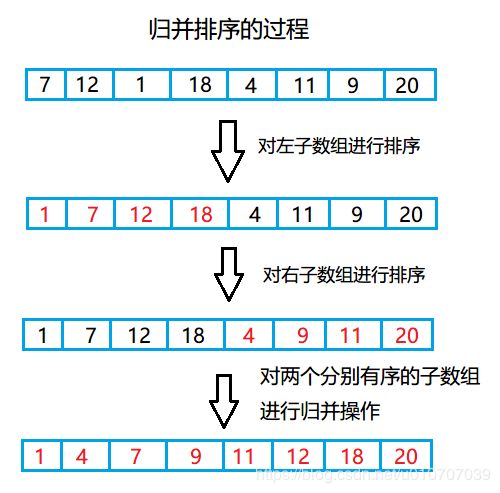
归并排序是基于“归并”这个操作得出的排序方法,所谓归并,就是将两个分别有序的数组合并(归并)成一个更大的有序的数组。那么归并排序就可以这样描述:要将一个数组排序,可以先(递归地)将它分成两半分别排序,然后将结果(两个分别有序的数组)归并成一个更大的有序的数组。
再来看看图解过程:
对左、右子数组进行排序的过程,其实也是通过归并操作来实现的,所以,实际上,真正在执行“排序”行为的是“归并”这个操作,归并排序就是递归地执行“归并”操作。接下来看看“归并”的过程。
一次归并的过程
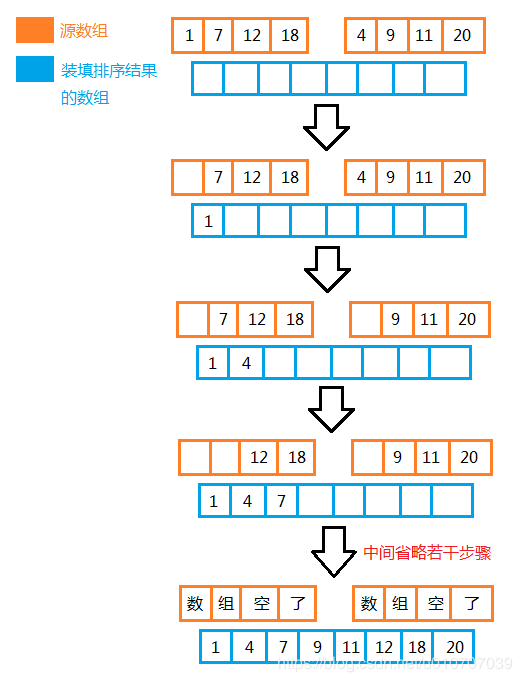
归并,就是将两个分别有序的子数组,合并成一个更大的有序的数组。一次归并的过程如下图所示(注意了是一次归并的过程,不是整个归并排序的过程) :
原地归并的抽象方法
归并排序里,一次归并的过程如前所述,很简单,但是这个思路只是纯理论式(理想化)的。因为“归并”是递归发生的行为(合并两个数组的代码会被多次调用),如果每一次归并都如前所述用一个新数组来装归并结果,整个归并的过程可能会创建大量临时数组,可能创建数组的时间花销比排序本身还大。为了解决这个问题而得出的另外一种实现归并过程的方法,就是原地归并的抽象方法。
实现思路
针对原始的归并方法存在的问题,解决的方法也并不复杂:通过反复利用同一个辅助数组来避免频繁地创建新数组。
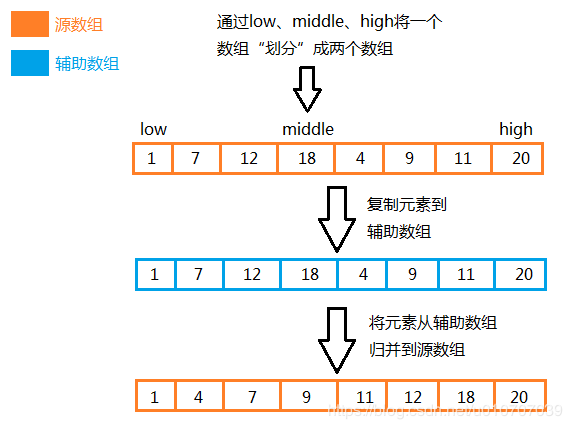
原地归并的抽象方法如下图所示:
说明:由于客户端一般都是传入一个待排序数组,不会传入两个数组,所以这里用角标low、middle、high将一个数组“划分”成两个数组。角标low ~ middle属于第一个子数组,角标middle+1 ~ high属于第二个子数组。
理解原地归并的抽象方法的重点在于:
虽然每一次的归并都会暂时使用辅助数组,但是都是用完立即“归还”,元素会被归并(排序)到源数组,每一次的归并行为结束后,辅助数组总是空的。所以递归的过程可以反复使用同一个辅助数组。
实现代码
原地归并的抽象方法实现代码(Java)如下:
void merge(int[] a, int low, int middle, int high){
int i = low, j = middle+ 1;
// 将源数组的元素复制到辅助数组
for(int k = lo; k <= hi; k++){
// 声明,aux[]表示一个定义在类里面(成员变量)的辅助数组
aux[k] = a[k];
}
// 执行归并过程
for(int k = low; k <= high; k++){
if(i > mid){
// 如果左边的子数组元素已经用尽
a[k] = aux[j++];
} else if (j > hi){
// 如果右边的子数组元素已经用尽
a[k] = aux[i++];
} else if (aux[i] < aux[j]){
a[k] = aux[i++];
} else {
a[k] = aux[j++];
}
}
}
以下开始分析这个算法的时间成本,主要分为“比较次数”和“访问数组的次数 ”。首先假设两个已经分别有序的子数组的长度加起来为N,即合并之后的数组长度为N。
时间成本-比较次数
最优情况:
如果左边的子数组最大的元素小于右边的子数组最小的元素,即a[middle] < a[middle+1],单次归并的比较次数达到最少。因为此时只有左边的子数组里的元素和右边的子数组的第一个元素参与比较,当左边的子数组元素用尽(全部被复制回了源数组),右边的子数组的元素不需要参与比较就能直接被复制回源数组。如果两个子数组的长度总是相等,那么这个最少的次数就是(1/2N) 。
最糟糕情况:
如果两个子数组各自最大的元素,分别是这N个元素里面最大的和次大的元素,即a[mid]、a[high]大于其它所有元素(它们两个谁比较大没有关系),单次归并的比较次数达到最多。因为此时每复制一个元素回源数组,都会发生一次比较,只有最大那个元素被复制回源数组前的那一次比较可以免去(因为没有可以比较的元素了)。这个最多的比较次数是(N-1) = O(N) 。
一个比较极端的情况:
前面关于最优情况的算数结果,是基于左右两个子数组的长度相等。考虑一个极端情况:两个子数组的长度之和仍为N,但是左边的子数组元素只有一个(右边N-1个),且这唯一一个元素小于右边子数组的所有元素,此时最少的比较次数为1。从算数的角度来讲,为了保证严谨性,我们列举了极端情况,但是从实际使用的情况来讲,左右两个子数组的长度大多数相等或者相差一个。即使是在迭代法实现的递归排序里,两个子数组的长度可能会相差较多(主要是每一轮循环的最后两个子数组),但是一般不会这么极端。
时间成本-访问数组的次数
首先定义诸如a[i]、a[j]这种读取算是进行了一次数组访问,诸如a[i] = a[j]、a[i] < a[j]这种语句算是进行了两次数组访问。那么一次归并操作要访问数组的次数主要在三个方面:
- 将元素从源数组复制到辅助数组:每复制一个元素进行了两次数组访问,一共2N次。
- 将元素从辅助数组复制回源数组:同上,一共2N次。
- 两个子数组的元素比较的次数:如前所述,最多是(N-1)次比较,一次比较算是进行了两次数组访问,一共(2N-2)次。最少比较1次,那访问数组2次。
所以访问数组的次数最多(6N-2)次,最少(4N+2)次。
此外还能得出一个算术关系:一次归并访问数组的总次数 = 用于复制的访问 + 用于比较的访问 = 4N + 比较次数*2。
空间成本
空间成本比较直观,就是辅助数组长度:N。
自顶向下的归并排序
自顶向下的归并排序,就是本文刚开头说的“(递归地)将数组分成两半分别排序,然后将结果(两个分别有序的子数组)归并成一个更大的有序的数组”。这个递归地将数组分半的过程,就是一个自顶向下的过程。
实现代码
自顶向下的归并排序的代码(Java)如下所示:
public class MergeSort{
private static int[] aux; // 归并操作用的辅助数组
// 供给外部客户端调用的归并排序方法
public static void sort(int[] a){
aux = new int[a.length];
sort(a, 0, a.length - 1);
}
// 内部进行递归操作的归并排序方法
private static void sort(a, int low, int high){
// 递归出口,当该条件成立,说明传进来的数组只有一个元素
// 而只有一个元素的数组,是不需要排序的,所以这是递归出口
if(high <= low){
return;
}
int middle = low + (high - low)/2;
sort(a, low, middle);
sort(a, middle + 1, high);
// merge()的实现见本文前面归并排序的抽象方法
merge(a, low, middle, high);
}
}
时间成本
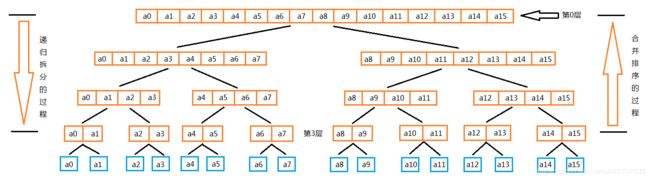
可以看出将一个数组拆分成两个数组是一个二分的过程,所以时间成本的分析可以用一个类似二叉树的结构图来进行(如果具备二叉树的基本知识,会更容易看懂这个分析过程)。如图:
树状图结构说明:
这棵二叉树从上往下看,是归并排序时递归拆分数组的过程,从下往上看,是归并操作对数组进行合并排序的过程。除了元素个数为1的结点,所有结点均表示一次归并操作的结果。如元素个数为2的结点,表示一次归并操作将两个元素为1的结点合并成一个元素个数为2的结点。再如一个元素个数为4的结点,表示一次归并操作将两个元素个数为2的结点合并成一个元素个数为4的结点。由于元素个数为1的结点不参与计算,所以用单独的颜色表示。
计算:
- 时间成本(不论是访问数组还是元素间的比较)主要都在merge()里面,也就是一次次的归并操作,所以时间成本的分析主要也是围绕归并操作来进行。
- 每一个元素个数不为1的结点,都表示一次归并操作的执行结果。这里要强调元素个数不为1的结点才算,最底下元素个数为1的那一层不看,因为它不是归并操作的结果,不需要也不应该参与计算。
- 记这棵树共有n层(再次强调不包括最底下元素个数为1的那一层,以上图为例就是4层),层的序号从0开始算,根结点记为第0层。在第k层,有(2k) 个结点,每个结点有(2(n-k))个元素。根据本文前面对归并操作比较次数的分析(通过归并操作的到一个长度为m的数组,需要进行O(m)次比较)。则通过归并操作得到一个结点需要进行(2(n-k))次比较,所以通过归并操作得到一层所有结点共需进行:(2k)*(2(n-k)) = (2n)次比较。
- 由于这棵树共有n层,所以比较的总次数为:n * (2n)。
- 对N个元素进行归并排序,根据二叉树的性质,树的层数n = lgN,用N替换n,得出对N个元素进行归并排序,在最糟糕的情况下,需要进行NlgN次比较。
- 再根据前面得出的数组访问次数和比较次数的关系(通过归并操作的到一个长度为m的数组,需要进行(4m+比较次数 * 2)次访问),那么得到一个结点共需进行(4 * 2(n-k) + 2 * 2(n-k)) = 6 * 2(n-k)次数组访问,则一层需要6 * 2(n-k) * (2k) = 6 * (2n),n层为6n * (2n)。以N代替n,数组访问6NlgN次。
以上结论是最糟糕的情况下时间成本的分析。简单说下最优情况,如果输入的数组原来就是排好序的,则对应最优情况,计算逻辑和上述基本一致,只是得到一个结点的比较次数由(2(n-k))变成(0.5 * 2(n-k)),对应的比较次数的最终结果变成0.5NlgN,数组访问次数的结果为5NlgN。
时间成本计算结论:不论是最优还是最糟糕的情况,不论是比较次数还是数组访问次数,虽然有常数因子的差异,但是最终的趋势都是O(NlgN)。
空间成本
空间成本就是辅助数组的长度,也就是客户端传入的数组长度:N。
自顶向下的归并排序的优化
只需要在代码里面做少许修改,就能明显优化归并排序,有以下三种优化方案:
- 对小规模子数组使用插入排序。
- 进行归并前判断数组是否已经有序。进行归并前判断数组是否已经有序。
- 不将元素复制到辅助数组,辅助数组也可以直接用来排序。不将元素复制到辅助数组,辅助数组也可以直接用来排序。
现在一个个展开来说。
对小规模子数组使用插入排序
不单单是归并排序,所有基于递归的操作,在待处理的元素个数较少的时候,递归的方法调用都会显得过于频繁。对于大规模数组的处理,归并排序效率明显高于基础排序算法(选择、插入、冒泡),但是元素个数越少,这种优势越不明显。对三两个元素进行递归操作,更加显得得不偿失。于是就有对小规模数组(元素个数小于特定长度)不再使用递归,而是使用基础排序算法(一般是插入,因为插入的性能好于其它几个)。代码修改也很简单,基于前面递归调用的sort()方法进行修改:
void sort(int[] a, int low, int high){
// 当待排序的数组长度缩小到BORDER时,递归调用转变为插入排序,BORDER的值可以由开发者自行定义
if(high <= low + BORDER){
// 假设这是一个已经实现了的插入排序
insertionSort(a, lo, hi);
return;
}
int middle = low + (high - low)/2;
sort(a, low, middle);
sort(a, middle + 1, high);
merge(a, low, middle, high);
}
所有长度小于BORDER的递归调用都免掉了。
判断数组是否已经有序
归并操作将两个分别有序的数组归并成一个更大的有序的数组,如果两个数组不但是分别有序,同时也互相有序了呢?如果a[mid] <= a[mid + 1],整个归并操作都是不需要的,甚至连merge()方法都不需要被调用。这种改动主要是在进行归并操作之前添加判断,可以基于前面递归调用的sort()方法进行修改:
void sort(int[] a, int low, int high){
// 递归出口,当该条件成立,说明传进来的数组只有一个元素
// 而只有一个元素的数组,是不需要排序的,所以这是递归出口
if(high <= low){
return;
}
int middle = low + (high - low)/2;
sort(a, low, middle);
sort(a, middle + 1, high);
// 如果两个子数组不但分别有序,同时也互相有序
if(a[mid] <= a[mid + 1]){
return;
}
// merge()的实现见本文前面归并排序的抽象方法
merge(a, low, middle, high);
}
如果两个数组不但是分别有序,同时也互相有序,对归并操作的调用就可以免掉了。
不将元素复制到辅助数组
归并操作(merge()方法)有相当一部分的时间成本在来回复制数组的操作上,这个对比较大小、排序操作本身并没有实际意义的操作,也是可以省略掉的,不过这就需要点技巧了。需要对进行归并操作的merge()方法和进行递归分组的sort()同时进行修改,先来看代码。
// 内部的,归并方法
private void merge(int[] src, int[] dst, int low, int middle, int high) {
int i = low, j = middle+1;
for (int k = low; k <= high; k++) {
if(i > middle){
dst[k] = src[j++];
} else if (j > high){
dst[k] = src[i++];
} else if (src[j] < src[i]){
dst[k] = src[j++];
} else{
dst[k] = src[i++];
}
}
}
// 内部的,递归调用的排序方法
private void sort(int[] src, int[] dst, int low, int high) {
if (high <= low){
return;
}
int middle = low + (high - lo) / 2;
// 重点在这里
// 每次向下一层进行递归的时候,将源数组(src)和目标数组(dst)的角色互换
sort(dst, src, low, middle);
sort(dst, src, middle+1, high);
merge(src, dst, low, middle, high);
}
// 供给外部调用的,启动整个排序过程的方法
public void sort(int[] a) {
int[] aux = a.clone();
sort(aux, a, 0, a.length-1);
}
上述代码主要改动点:
- 首先在merge()里面进行修改,不再使用辅助数组,而是直接将元素从源数组(src)归并到目标数组(dst),源数组和目标数组由递归的sort()指定。
- 其次是对sort()进行修改,在每一层向下一层进行递归的时候,将源数组和目标数组的角色互换。需要注意的是,本层对merge()的调用,还是要保持源数组和目标数组的关系和传进来的时候一致。其次是对sort()进行修改,在每一层向下一层进行递归的时候,将源数组和目标数组的角色互换。需要注意的是,本层对merge()的调用,还是要保持源数组和目标数组的关系和传进来的时候一致。
- 最后就是在供给外部调用的sort(int[] a)方法里,在启动内部的sort(int[] src, int[] dst, int low, int high)时,要注意将客户端传进来的待排序的数组当作目标数组传进去,将辅助数组当作源数组传进去。最后就是在供给外部调用的sort(int[] a)方法里,在启动内部的sort(int[] src, int[] dst, int low, int high)时,要注意将客户端传进来的待排序的数组当作目标数组传进去,将辅助数组当作源数组传进去。
综合优化——同时优化三个地方
为了方便理解而分开描述的优化方案叙述完了,现在来看同时对这三个地方进行修改的方案,这里不再做过多的描述,直接看代码。(注意在启动递归调用之前对数组的复制操作,这是“不将元素复制到辅助数组”的优化方案能实现的前提)
// 执行归并操作的方法
private void merge(int[] src, int[] dst, int lo, int mid, int hi) {
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++) {
if (i > mid){
dst[k] = src[j++];
} else if (j > hi){
dst[k] = src[i++];
} else if (src[j] < src[i]){
dst[k] = src[j++];
} else{
dst[k] = src[i++];
}
}
}
// 递归的sort()方法
private void sort(int[] src, int[] dst, int lo, int hi) {
// 小规模数组使用插入排序
if (hi <= lo + BORDER) {
insertionSort(dst, lo, hi);
return;
}
int mid = lo + (hi - lo) / 2;
sort(dst, src, lo, mid);
sort(dst, src, mid+1, hi);
// 对于已经互相有序的两个子数组,跳过归并操作,直接从源数组复制到目标数组
if (src[mid] <= src[mid + 1]) {
System.arraycopy(src, lo, dst, lo, hi - lo + 1);
return;
}
merge(src, dst, lo, mid, hi);
}
// 供客户端调用来启动归并排序的方法
public void sort(int[] a) {
// 注意这里的clone()方法,“不将元素复制到辅助数组”的优化方案要能正确执行,
// 关键在于在进行递归之前,就复制了一个数据内容和原数组一样的辅助数组,这样才不会混乱。
int[] aux = a.clone();
sort(aux, a, 0, a.length-1);
}
自底向上的归并排序
归并排序有两种实现方法,一种是比较符合直观逻辑的递归方法,称为自顶向下的归并排序,也就是前文所述的全部内容。另一种是迭代实现的方法,称为自底向上的归并排序。现在开始来讲这个。
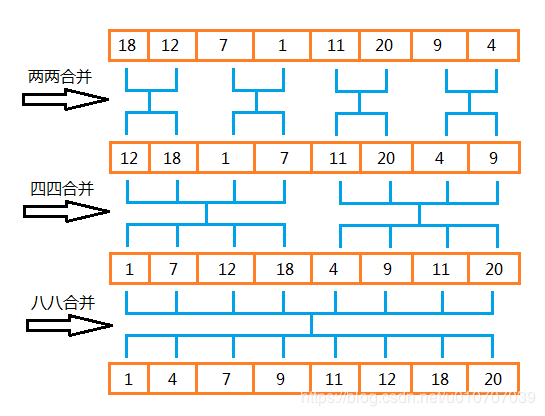
查看本文前面自顶向下的归并排序的示意图,递归的尽头都是将数组拆到只剩1个元素,所以merge()方法也是从两个长度为1的数组开始归并,等凑出两个长度为2的数组,再将两个长度为2的数组归并,以此类推。如果客户端传入的初始数组长度不是2的次幂,可能中间子数组的长度略有不同,比如待归并的两个子数组的长度是3和2,但是整个程序的执行逻辑和过程都是一样的,都是从最小的1个元素开始归并,接着将得到的结果继续归并。循着这样一个思路,我们也可以不通过递归调用来对元素进行分组,而是通过循环来对元素进行分组,只要merge()方法所接受的数组长度从1开始,按照1、2、4这样一点点递增就可以了。执行逻辑如下图:
整个过程看起来和自顶向下的归并排序明显不同,但是有一点本质没变:归并的操作总是从只有1个元素的数组开始,逐步增大,最后完成整个数组的排序。
代码
自底向上的归并排序代码十分简洁,但是重要的是理解这段代码是怎么执行起来的:
/* 自底向上(迭代法)的归并排序*/
void sort(int[] a){
int N = a.length;
// 创建同待排序的数组同样大小的辅助数组
aux = new int[N];
// size表示每次归并时被归并的单个子数组的大小,注意不是归并后的数组大小
for(int size = 1; size < N; size = size + size){
for(int low = 0; low < N - size; low += size + size){
merge(a, low, low + size - 1, Math.min(low + size + size - 1, N - 1));
}
}
}
代码的执行流程如前面示意图所示,比较有必要理清楚的地方是两个循环里面各个边界、叠加值、以及传给merge()的参数值都是怎么算出来的。
如果你真的搞懂了自底向上的归并排序的思路,应该能理解两个循环的职责:
内层循环在控制每次传给merge()的两个子数组是哪两个,主要是通过控制low来设定起点。外层循环在控制每次待排序的子数组的尺寸,从1开始,每次翻倍。
职责都理清楚了,现在首先来看看外层循环是怎么控制的:
- size的含义:这里需要重点说明,将两个子数组归并成一个更大的数组,size是归并前单个子数组的大小,不是归并后的大数组的大小。
- size初始值:待排序的子数组的尺寸从1开始,没有什么好解释的。
- size叠加值:根据自底向上的归并排序思路,待排序数组的尺寸成倍增长。
- size边界:当size刚好等于(或大于)N,说明刚刚完成了最后一次归并,即最大的两个子数组的归并操作,反过来只有size
接着来看内层循环是怎么控制的:
- low初始值:每一次归并结束,待排序数组尺寸翻倍后,都是要从头开始遍历排序的,所以low从0开始。
- low叠加值:size是待排序的子数组的尺寸,所以每次归并完两个子数组后,low是叠加2倍的size而不是1倍的size。
- low边界:主要是根据low+size
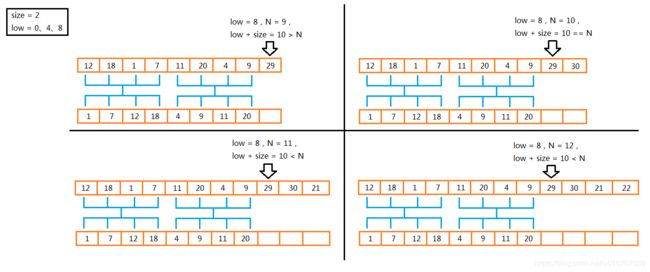
如上图所示,这里有四个数组在进行自底向上的归并排序,它们的元素几乎一样,也处在相同的排序阶段(size = 2,即每次循环将两个长度为2的子数组归并成一个长度为4的数组)。low会先后等于0、4、8。当low等于0、4时,这四个数组的行为是一样的。当low等于8时,本该进行第三次归并操作,但是对于上面的两个数组,他们不需要(也没法)进行第三次归并操作,因为剩余的元素凑不出第二个子数组(第二个子数组一个元素都没有),而一个子数组本来就是有序的,此时low+size>=N。再看下面的两个子数组,它们剩余的元素超出一个子数组的长度,虽然不一定能凑满第二个子数组,但是第二个子数组还是有元素的,所以它们需要被归并。所以只有low+size 继续看传入merge()方法的参数是怎么计算的: 当size=2,low=8时,即将进行第三次归并操作。此时剩余的元素个数超出一个子数组的长度(即第二个子数组有元素),但是第二个子数组凑不满,如果直接用high=low+size+size-1的话,数组就越界了,所以才有Math.min(low+size+size-1, N-1)这个取较小值的操作。如果客户端最初传入的数组长度刚好是2的指数,则high=low+size+size-1总是对的。如果客户端最初传入的数组长度不是2的指数,每个size值对应的循环,进行到最后两个子数组的归并操作时,有可能出现第二个子数组凑不满的情况,此时high=low+size+size-1会导致越界,此时high=N-1才是第二个子数组的边界。 至此关于自底向上的归并排序各个参数的分析,结束。 本文详细介绍了关于归并排序的方方面面,从思想的角度来说,分为两个大方向:一是基于递归思想实现的自顶向下的归并排序,二是基于迭代思想实现的自底向上的归并排序。 不论递归还是迭代,实现排序的核心都是归并操作,因此本文最前面的篇幅都在介绍归并操作,不仅仅是介绍代码,还详细分析了时间成本。 自顶向下的归并排序占据较大篇幅,其实它本身不难理解,只是其中可以优化的地方比较多,所以占的篇幅多些。 自底向上的归并排序相对没那么好理解,所以花了较多篇幅在代码的分析上面,包括对重要参数的初始值、变化量、边界值进行分析。本文没有对自底向上的归并排序做时间成本的分析,因为迭代的过程显然是比递归的过程效率更高,而且两者的主要时间成本都在归并操作上面,由于分析了递归的排序,就没有分析迭代的排序。
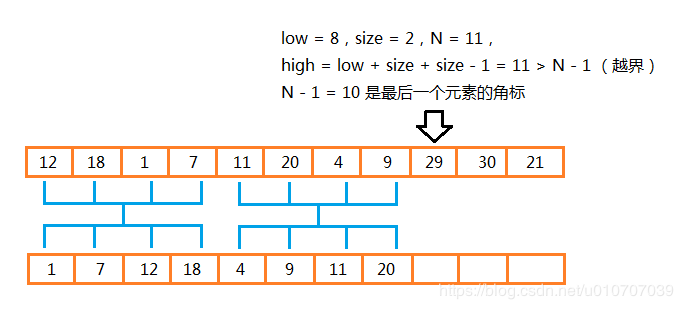
传入merge()的几个参数的含义和之前的是一样的,包括数组、low、middle、high,那么前面两个参数就没什么好解释的了,主要看看后面两个。由于size是待排序的子数组的尺寸,所以middle=low+size-1。同样的由于size是待排序的子数组的尺寸,所以high=low+size+size-1。那么这个N-1和数学函数Math.min()是怎么回事?来看以下这种情况:总结