普利姆算法(Prim)解决修路问题
普利姆算法(Prim)解决修路问题
普利姆算法(Prim)
使用普利姆算法(Prim)求最小生成树
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。

最小生成树
(1)给定一个带权的无向连通图,使边上权的总和为最小。
(2)N个顶点,一定有N-1条边
(3)包含全部顶点
(4)N-1条边全在图中
具体实现方法:
先选中一个节点为初始节点作为一个整体,在剩下所有节点与该节点相连的边中,选择最短的一条边,这条边的节点与之前的节点一起作为一个整体,在新加入这个整体的那个节点,在继续寻找与该节点相连的边中最短的一个,将这个节点的边与之前的节点一起作为一个整体,以此类推,直到遍历完所有的节点。
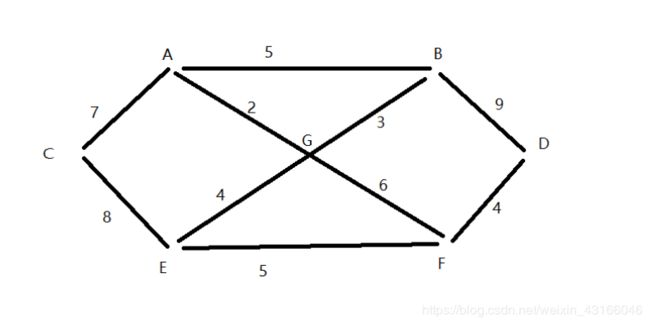
胜路村现在有七个村庄(A,B,C,D,E,F,G),现在需要修路把七个村庄连通
各村庄之间的距离由边线表示
如何保证个村庄都能连通,并且修建里程数最短
尽可能少的路线,连通,且里程数最短
选择A作为出发顶点,步骤如下:
< A > -> G
< A,G > -> B
< A,G,B> -> E
< A,G,B,E > -> F
< A,G,B,E,F > -> D
< A,G,B,E,F,D > < A > -> C
< A,G,B,E,F,D,C >
package nuc.sw.test;
import java.util.Arrays;
public class Prim {
public static void main(String[] args) {
// TODO Auto-generated method stub
char[] data=new char[]{'A','B','C','D','E','F','G'};
int verxs = data.length;
//邻接的关系使用二维数组表示10000表示不联通
int[][] weight=new int[7][];
int N=1000;
weight[0]=new int[]{N,5,7,N,N,N,2};
weight[1]=new int[]{5,N,N,9,N,N,3};
weight[2]=new int[]{7,N,N,N,8,N,N};
weight[3]=new int[]{N,9,N,N,N,4,N};
weight[4]=new int[]{N,N,8,N,N,5,4};
weight[5]=new int[]{N,N,N,4,5,N,6};
weight[6]=new int[]{2,3,N,N,4,6,N};
//创建MGraph对象
MGraph mgraph = new MGraph(verxs);
//创建MinTree对象
MinTree minTree = new MinTree();
minTree.createGraph(mgraph, verxs, data, weight);
minTree.showgGraph(mgraph);
minTree.prim(mgraph, 0);
}
}
/**
* 创建最小生成树
* 2019年7月11日
* @author Wang-peiaaa
*
*/
class MinTree {
//创建图的邻接矩阵
/**
*
* @param graph 传进来的图对象
* @param verx 图的节点个数
* @param data 个顶点得知值
* @param weight 图的邻接矩阵
*/
public void createGraph(MGraph graph , int verx , char[] data , int[][] weight) {
int i , j;
for ( i = 0; i < verx; i++) {//节点
graph.data[i] = data[i];
for ( j = 0; j < verx; j++) {
graph.weight[i][j] = weight[i][j];
}
}
}
//显示出邻接矩阵
public void showgGraph(MGraph graph) {
for (int[] link : graph.weight) {
System.out.println(Arrays.toString(link));
}
}
//编写prim算法 最小生成树
/**
*
* @param graph 图
* @param v 表示从图的第几个顶点开始生成 A->0 , B->1
*/
public void prim(MGraph graph , int v) {
//标记顶点是否被访问过, 默认为0
int visited[] = new int[graph.verxs];
//表示这个节点已经访问过
visited[v] = 1;
//记录节点下标
int h1 = -1;
int h2 = -2;
int minWeight = 10000;
for(int k = 1 ; k < graph.verxs ; k++) {
//确定每一次生成的子图和那个节点最近
//i表示已经被访问过的节点,j表示未被访问过的节点
for(int i =0 ; i < graph.verxs ; i++) {
for(int j = 0 ; j< graph.verxs ; j++) {
if(visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {
//寻找访问过的节点和未访问过的节点之间最小的权值
minWeight = graph.weight[i][j];
h1 = i;
h2 = j;
}
}
}
System.out.println("边<" + graph.data[h1] +","+ graph.data[h2] + "> 权值:" + minWeight);
//将这个点标记为已访问
visited[h2] = 1;
minWeight = 10000;
}
}
}
class MGraph {
int verxs; //表示图的节点个数
char[] data;//存放节点数据
int[][] weight;//存放边,邻接矩阵
public MGraph(int verxs) {
this.verxs=verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
}
最终结果
边
边
边
边
边
边
