Codeforces Round #629 (Div. 3)题解

题意

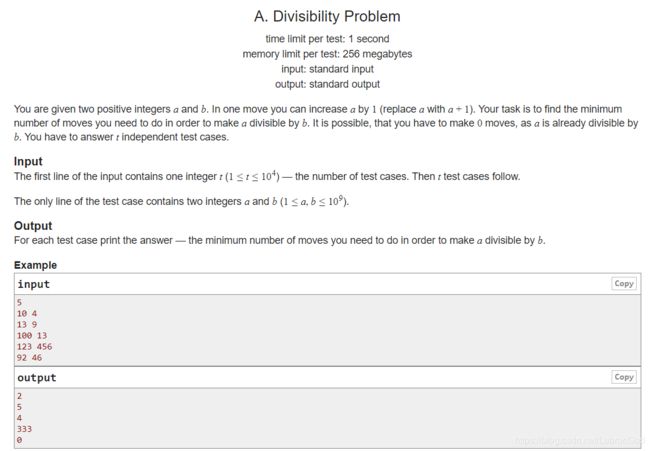
给你两个数a,b,你可以使a增大,求增大多少能使a整除b

AC代码

#include
#include
using namespace std;
int main()
{
   int t;
   cin>>t;
   while(t--)
   {
  	   int a,b;
  	   cin>>a>>b;
  	   if(a%b==0) {//能整除就最好咯啥都不干出0
   	       cout<<0<<endl;
  	   } else if(a>b) {//不能整除但比b大，算出能整除b且大于a的最小值减去a即可
     	   cout<<(int)(a/b+1)*b-a<<endl;
       } else if(a<b) {//比b还小，补到和b一样大即可
   	       cout<<b-a<<endl;
  	   }
   }
}

题意

给你字符串长度n和k，你可以使用两个字符b和n-2个字符a，问按照b往前走（样例那样）排下去，第k个字符串是什么。

思路

就是模拟将两个b往前移，一次只能移动一步，把k步时的b的位置记录输出即可。

AC代码

#include
#include
using namespace std;
typedef long long ll;
int main()
{
	int t;
	cin>>t;
	while(t--)
	{
		int n,m;
		cin>>n>>m;
		int cnt=0;
		int i,j;
		for(i=n-1;i>=1;i--) {
			for(j=n;j>i;j--) {
				cnt++;
				if(cnt==m) break;
			}
			if(cnt==m) break;
		}
		for(int k=1;k<=n;k++) {
			if(k==i||k==j) {
				cout<<"b";
			}else {
				cout<<"a";
			}
		}
		cout<<endl;
	}
}

题意

给你一个数x，求a，b，能使(a+b)%3=x,且在满足条件的所有a，b中，a,b中的最大值最小

思路

先一波无脑拆分，2拆成1，1；1拆成1，0；0就0，0；然后从高位开始遍历拆分后的c,d数组出现第一个不同的元素后，将不同的那一位大的后面剩下的值都加到另外一个数组对应的位上，这样就使得最大值最小了。

AC代码

#include
#include
using namespace std;
int a[50050],c[50050],d[50050];
int main()
{
	int t;
	cin>>t;
	while(t--)
	{
		int n;
		cin>>n;
		memset(c,0,sizeof(c));
		memset(d,0,sizeof(d));
		char ch;
		for(int i=0;i<n;i++) {
			cin>>ch;
			a[i]=ch-'0';
		}
		for(int i=0;i<n;i++) {//无脑拆分
			if(a[i]==1) {
				c[i]=1;d[i]=0;
			} else if(a[i]==2) {
				c[i]=1;d[i]=1;
			} else if(a[i]==0) {
				c[i]=0;d[i]=0;
			}
		}
		for(int i=0;i<n;i++) {//从高位开始遍历
			if(c[i]>d[i]) {//当出现不同的时候
				for(int j=i+1;j<n;j++) {//把该位之后的元素全都丢给另一数组
					if(c[j])  {
						d[j]+=c[j];
						c[j]=0;//使得最大值最小化
					}
				}
				break;
			}else if(d[i]>c[i]) {//同上步骤
				for(int j=i+1;j<n;j++) {
					if(d[j]) {
						c[j]+=d[j];
						d[j]=0;
					}
				}
				break;
			}
		}
		for(int i=0;i<n;i++) {
			cout<<c[i];
		}
		cout<<endl;
		for(int i=0;i<n;i++) {
			cout<<d[i];
		}
		cout<<endl;
	}
}

题意

给一个数组，给他染色，如果t[i]!=t[i-1],则t[i]和t[i-1]不能染同一种颜色，若t[i]=t[i-1],你可以染同一种颜色，也可以染成不同颜色的。求染色用的颜色最少是多少及每个元素的颜色是什么。

思路

把重复的认为是一个数都涂一个色，那么就分成了偶数个和奇数个的问题
偶数个就直接1212，重复部分颜色相同即可
奇数个又分为
①有重复，某一个重复部分变色一次就和偶数一样了
②无重复，也就是1 2 3这样的，前面直接按照偶数输出，末尾输出3就可以了

AC代码

#include
#include
#include
using namespace std; 
int a[200020];
int main() 
{
    int T;
    cin>>T;
    while (T--) 
    {
        int n;
        cin>>n;
        memset(a,0,sizeof(a));
        int num=1,flag=1,t=0;
        for (int i=0; i<n; i++) {
            cin>>a[i];    
            if (i>=1 && a[i]==a[i-1]) {//如果相邻有重复 
                flag=0;
                t=i;//记录重复位置的靠后的那个的下标 
            }
            if (i>=1&&a[i]!=a[i-1]) {
                if (i==n-1 && a[i]==a[0]) {//判断首尾相邻是否重复 
                    flag=0;
                    t=i;
                }
                else {
                    num++;//相邻但不重复的元素个数 ，相邻重复的就被看成一个元素了 
                }
            }
        }
        if (num == 1) {//如果全相等 
            cout<<1<<endl;//只涂一色 
            for (int i=0; i<n; i++) {
                cout<<1<<" ";
            }
            cout<<endl;
        }
        else if (num % 2 == 0) {//若无相邻相等且为偶数个 直接无脑121212 
            int color = 1; 
            cout<<2<<endl<<color<<" "; 
            for (int i=0; i<n-1; i++) {
                if (i!=n-1&&a[i]!=a[i + 1]) {
                    if (color==2) {
                        cout<<1<<" ";
                    }
                    else {
                        cout<<2<<" ";
                    }
                }
            }
        cout<<color<<endl;
        }
        else {//为奇数个元素 
            if (flag==0) {//且有相邻重复的 
                int color=1;
                cout<<2<<endl<<color<<" ";
                for (int i=0; i<n; i++) {
                    if ((i!=n-1 && a[i]!=a[i + 1])||i==t-1) {//当当前元素与下一元素不同或遍历到重复的那坨的开头时改色 
                        if (color==2) {
                            cout<<1<<" ";
                        }
                        else {
                            cout<<2<<" ";
                        }
                    }
                }
            cout<<endl;
            }else{//没有相邻相同且为奇数在偶数基础上把最后一位改成3即可 
                int color=1;
                cout<<3<<endl<<color<<" ";
                for (int i=0; i<n-1; i++) {
                    if (i!=n-1 && a[i]!=a[i + 1]) {
                        if (color==2) {
                            cout<<1<<" ";
                        }
                        else {
                            cout<<2<<" ";
                        }
                    }
                }
            cout<<3<<endl;
            }
        }
    }
    return 0;
}

题意

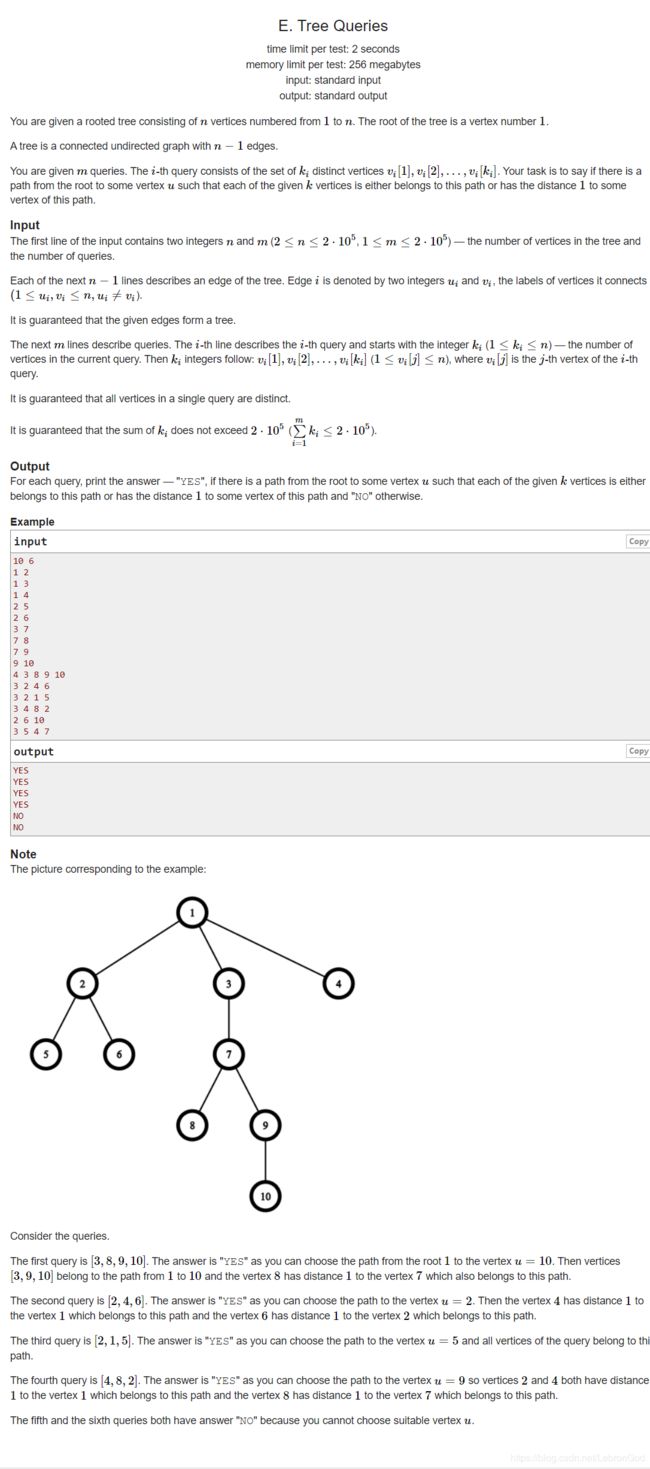
给你一棵树，和m个查询，每个查询描述了一个点集合（第一位是点集合个数），问这个点集合的在不在一条从根节点1开始到某一点的路径上（或离这条路距离为1）。

思路

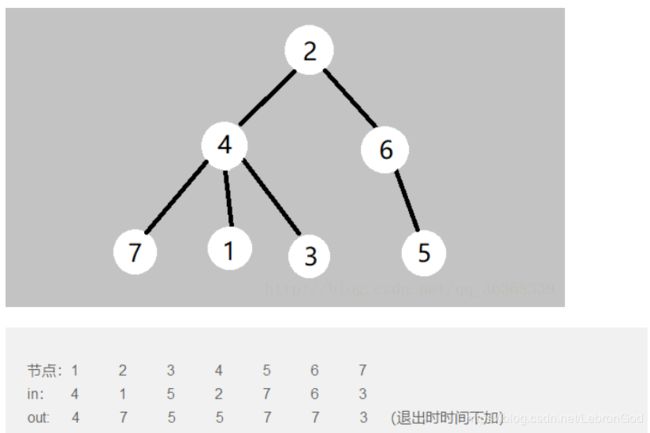
根据到这条路径的距离不大于一可以得出，要么这个点就在这条路上要么就是他的父亲在这条路上，接下来的难点就是如何知道他们的父亲是不是在一条路径上，思考一波（上网查 ）之后，可以搞一手dfs记录时间戳，用dfs遍历一遍这棵树，进入到x节点有一个in时间戳，递归退出时有一个out 时间戳，x节点的两个时间戳之间遍历到的点，就是根为x的子树的所有节点，他们的dfs进入时间戳是递增的。如果在一条路径上，那么dfs过程中这些点的max(in[x])和min(out[x])应该是相等的。即v在不在1到u路径上，可以等价于u是不是v的子树。

AC代码

#include
#include
#include
using namespace std;
const int maxx=2e5+10;
vector<int> G[maxx];
int in[maxx],out[maxx],fu[maxx];
int cnt=0;
void dfs(int u,int par) {
	fu[u]=par;//存储这一对父子关系
	in[u]=++cnt;//存储访问顺序
	for(int i=0;i<G[u].size();i++) {
		int u1=G[u][i];
		if(u1==par) {//父节点就不搜了
			continue;
		} else {
			dfs(u1,u);
		}
	}
	out[u]=cnt;//搜到叶节点后这条路结束
}
int main()
{
	int n,T,u,v;
	cin>>n>>T;
	for(int i=1;i<n;i++) {//建图
		cin>>u>>v;
		G[u].push_back(v);
        G[v].push_back(u);
	}
	dfs(1,0);//从根节点开搜
	while(T--)
	{
		int t;
		cin>>t;
		int l=1,r=n;
		while(t--)
		{
			int ask;
			cin>>ask;
			if(ask!=1){
				ask=fu[ask];//问题改成他的父节点在不在一条路上
			}
			l=max(l,in[ask]);//最后进来的
			r=min(r,out[ask]);//最先出去的
		}
		if(l<=r) {//最后进来的在最先出去的之前即可，说明这一波查询的节点的父节点在一条路上
			cout<<"YES"<<endl;
		} else {
			cout<<"NO"<<endl;
		}
	}
	return 0;
}

题意

给定一个数组a，每次操作你可以使最大值减一或最小值加一，问经过最少多少次这样的操作后，数组a中有k个值相等

思路

先想一个问题这最后k个相等的值会是a数组中不存在的值吗？

答案是不会的，因为如果最后的值在a中不存在，就意味着我们要由0个构造出k个，但最后的值是a中的某个值的话，我们至少都有一个了啊，那是由1+x个到k个明显后者优于前者。

由于只能对最大最小值操作，那么如果操作完后有k个一样的值n，那么这k个值一定是从n+1或者n-1操作得到的，如果你要执行+1这个操作得到n，那就意味着所有的小于n的值都先变成了n-1，执行-1同理都先变成了n+1。因此我们先把将小于n的所有数都变成n−1 的最少步数 和 将大于n 的所有数都变成 n+1 的最少步数 算出来存起，这个先记着。
然后遍历最后可能的n值（即a数组中不重复的值），如果数量大于等于k，那最好一步都不用做输出0，不足则用+1或-1操作补齐（并将操作步数累加）有以下三种情况
① +1 -1 一起上：那就要把最大最小值都搞到n+1和n-1再看每差一个就加一（离成功只有一步之遥）
②+1：把小于当前值的都搞到n-1，前提是他是够的，加上自带的要大于等于k个
③-1：把大于当前值的都搞到n+1，前提是他是够的，加上自带的要大于等于k个

AC代码

#include
#include
using namespace std;
typedef long long ll;
const int maxx=2e5+10;
ll ans=1e18; 
int a[maxx]; 
int num[maxx],cnt[maxx];//num数组存储a中的不重复元素，cnt存储对应值的个数 
ll add[maxx],reduce[maxx],les[maxx],more[maxx];//add存的是通过+1操作的最少步骤，reduce为-1，les为小于当前值有多少个，more同理
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=0;i<n;i++) {
		cin>>a[i];
	}	
	sort(a,a+n);
	int e=0,k=0;
	for(int i=0;i<n;i++) {
		e++;//相同则一直累加 
		if(a[i]!=a[i+1]) {
			num[k]=a[i];
			cnt[k++]=e;//当前a[i]的相同的个数 
			e=0; 
		}
	}
	for(int i=1;i<k;i++)//递推先打出add和reduce 
	{
		int M=num[i]-num[i-1]; 
		add[i]=add[i-1]+les[i-1]*M+cnt[i-1]*(M-1);//当前值只需要变到num[i]-1就行了 
		les[i]=les[i-1]+cnt[i-1];//小于i的数量为小于i-1和i-1的数量之和 
	}
	for(int i=k-2;i>=0;i--)
	{
		int M=num[i+1]-num[i];
		reduce[i]=reduce[i+1]+more[i+1]*M+cnt[i+1]*(M-1);
		more[i]=more[i+1]+cnt[i+1];
	}
	for(int i=0;i<k;i++) {
		if(cnt[i]>=m){//已有m个 
			cout<<0<<endl;
			return 0;
		}
		int cha=m-cnt[i];//还欠多少个
		if(i>0 && i<k-1) {//同时进行+1-1操作的
			ans=min(ans,add[i]+reduce[i]+cha);
		} 
		if(i>0 && les[i]>=cha) {//只进行+1操作 
			ans=min(ans,add[i]+cha);
		}
		if(i<k-1 && more[i]>=cha) {//只进行-1操作 
			ans=min(ans,reduce[i]+cha);
		}
    } 
    cout<<ans<<endl;
	return 0; 
} 

做题解不易点个赞呗