【2020-MOOC-浙江大学-陈越、何钦铭-数据结构】图(第七周的笔记和编程作业)
文章目录
- 〇、前言
- 一、复习
- 二、哈利波特的考试
- 三、课后题
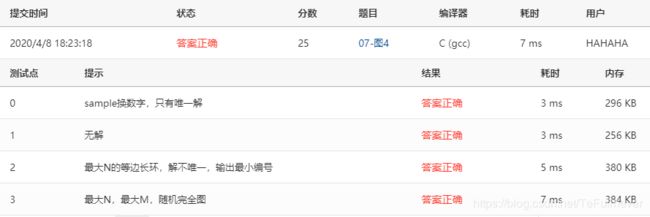
- 1、07-图4 哈利·波特的考试 (25分)
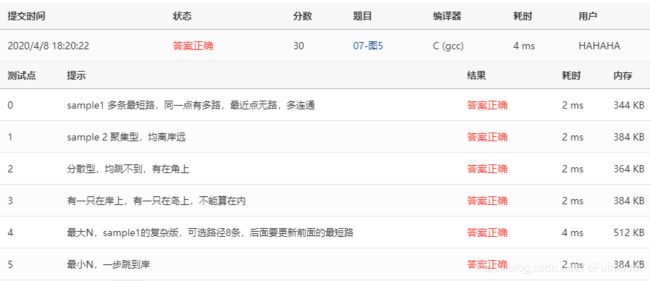
- 2、07-图5 Saving James Bond - Hard Version (30分)
- 3、07-图6 旅游规划 (25分)
- 总结
〇、前言
这两周开始跟着【MOOC-浙江大学-陈越、何钦铭-数据结构】进行数据结构与算法的学习,特此记录复习一下,虽然记不住,但是一直记一直记一直记,成为复读机就好了。

一、复习
这周主要是复习,同时有几个题,今天终于找到了自己数据结构学不懂的问题了,一个大佬说的一句话,让我恍然大悟的感觉。
其实就是C++或者C语言学的不好,基础太差,具体来说,就是代码量不够,导致没法自己解决问题,从而导致了写不出来代码,所以准备刷一下PTA。
二、哈利波特的考试
三、课后题
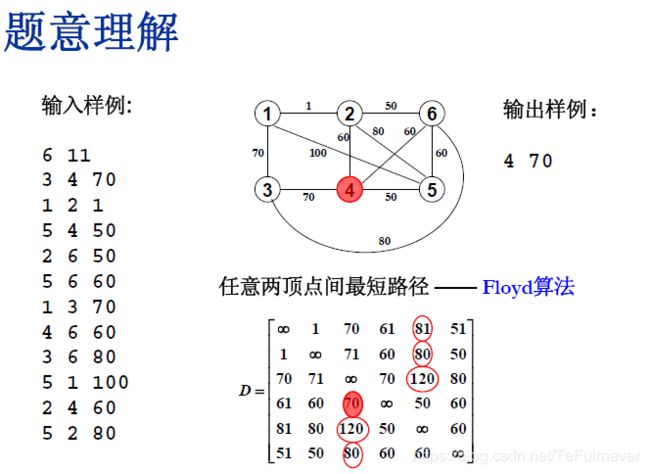
1、07-图4 哈利·波特的考试 (25分)
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
输出样例:
4 70
#include */
WeightType Weight; /* 权重*/
};
typedef PtrToENode Edge;
/* 图结点的定义*/
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数*/
int Ne; /* 边数*/
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵*/
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型*/
void FindAnimal( MGraph Graph ){
WeightType D[MaxVertexNum][MaxVertexNum], MaxDist, MinDist;
Vertex Animal, i;
Floyd( Graph, D );
MinDist = INFINITY;
for ( i=0; i<Graph->Nv; i++ ) {
MaxDist = FindMaxDist( D, i, Graph->Nv );
if ( MaxDist == INFINITY ) { /* 说明有从i无法变出的动物*/
printf("0\n");
return;
}
if ( MinDist > MaxDist ) { /* 找到最长距离更小的动物*/
MinDist = MaxDist; Animal = i+1; /* 更新距离,记录编号*/
}
}
printf("%d %d\n", Animal, MinDist);
}
WeightType FindMaxDist( WeightType D[][MaxVertexNum],Vertex i, int N ){
WeightType MaxDist;
Vertex j;
MaxDist = 0;
for( j=0; j<N; j++ ) /* 找出i到其他动物j的最长距离*/
if ( i!=j && D[i][j]>MaxDist )
MaxDist = D[i][j];
return MaxDist;
}
MGraph CreateGraph( int VertexNum ){
/* 初始化一个有VertexNum个顶点但没有边的图*/
Vertex V, W;
MGraph Graph;
Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图*/
Graph->Nv = VertexNum;
Graph->Ne = 0;
/* 初始化邻接矩阵*/
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V=0; V<Graph->Nv; V++)
for (W=0; W<Graph->Nv; W++)
Graph->G[V][W] = INFINITY;
return Graph;
}
void InsertEdge( MGraph Graph, Edge E ){
/* 插入边 */
Graph->G[E->V1][E->V2] = E->Weight;
/* 若是无向图,还要插入边 */
Graph->G[E->V2][E->V1] = E->Weight;
}
MGraph BuildGraph(){
MGraph Graph;
Edge E;
int Nv, i;
scanf("%d", &Nv); /* 读入顶点个数*/
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图*/
scanf("%d", &(Graph->Ne)); /* 读入边数*/
if ( Graph->Ne != 0 ) { /* 如果有边*/
E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点*/
/* 读入边,格式为"起点终点权重",插入邻接矩阵*/
for (i=0; i<Graph->Ne; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
E->V1--; E->V2--;
/* 注意:如果权重不是整型,Weight的读入格式要改*/
InsertEdge( Graph, E );
}
}
return Graph;
}
void Floyd( MGraph Graph, WeightType D[][MaxVertexNum] ){
Vertex i, j, k;
/* 初始化*/
for ( i=0; i<Graph->Nv; i++ )
for( j=0; j<Graph->Nv; j++ ) {
D[i][j] = Graph->G[i][j];
}
for( k=0; k<Graph->Nv; k++ )
for( i=0; i<Graph->Nv; i++ )
for( j=0; j<Graph->Nv; j++ )
if( D[i][k] + D[k][j] < D[i][j] ) {
D[i][j] = D[i][k] + D[k][j];
}
}
int main(){
MGraph G = BuildGraph();
FindAnimal( G );
return 0;
}
2、07-图5 Saving James Bond - Hard Version (30分)
17 15
10 -21
10 21
-40 10
30 -50
20 40
35 10
0 -10
-25 22
40 -40
-30 30
-10 22
0 11
25 21
25 10
10 10
10 35
-30 10
Sample Output 1:
4
0 11
10 21
10 35
Sample Input 2:
4 13
-12 12
12 12
-12 -12
12 -12
Sample Output 2:
0
#include3、07-图6 旅游规划 (25分)
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40
#include 总结
刷题刷题刷题!!!
数据结构,陈越等,浙大课程原版的书,需要的可以去公众号自取。

如果想要更多的资源,欢迎关注 @我是管小亮,文字强迫症MAX~
回复【数据结构】即可获取我为你准备的大礼!!!
想看更多文(段)章(子),欢迎关注微信公众号「程序员管小亮」~