树(或有向无环图)中根结点到所有叶子的路径
问题:假设现在有一棵树,注意这里的树不一定是二叉树(也即可以是多叉树),我们希望枚举出从根结点到每一个叶子结点的路径,这个算法该如何实现?
下面的例子主要采用Python来实现。为了方便构建一棵树(还有后面的有向图),这里直接使用Python中NetworkX包(NetworkX是一个用Python语言开发的图论与复杂网络建模工具)。首先引入必要的包。
import copy
import networkx as nx
from collections import deque
import matplotlib.pyplot as plt
%matplotlib inline构建一棵多叉树 T:
T = nx.DiGraph()
T.add_nodes_from(['a','b','c','d','e','f','g','i'])
T.add_edges_from([('a','b'),('b','c'),('c','d'),('d','e')])
T.add_edges_from([('b','f'),('f','g'),('f','h'),('b','i')])
nx.draw(T, with_labels=True)
plt.show()执行上述代码,所得之结果如下图所示(注意,树也可以看成是一种特殊的有向图。这里使用的NetworkX主要是用来处理图的,所以绘制出来的树并不像通常我们看到的树那么层次分明,但是本质上它们是一致的):
显然,从根节点a到叶子结点e、g、h、i的路径有[a->b->c->d->e]、[a->b->f->g]、[a->b->f->h]、[a->b->i]。
具体(非递归)算法的设计思路可以从树的深度优先遍历中获得启示。唯一需要注意的是,如果在某结点处存在分叉,我们需要维护额外一个栈结构来保存分叉点前面已经得到路径。下面给出具体实现的代码,注意这是一个非递归的实现:
majorStack = deque([])
minorStack = deque([])
listoflists = []
a_list = []
entry_node = 'a'
def find_all_paths():
max_times = 0
minorStack.append(entry_node)
popCount = {}
while minorStack:
minLast = minorStack.pop()
majorStack.append(minLast)
a_list.append(minLast)
current_s_nodes = list(T.successors(minLast))
if current_s_nodes:
for element in current_s_nodes:
minorStack.append(element)
majLast = majorStack[-1]
#Loop condition:tos is a leaf OR all children of tos have been accessed
while( not list(T.successors(majLast)) or
( popCount.get(majLast, -1) == len(list(T.successors(majLast))))):
last = majorStack.pop()
if majorStack:
majLast = majorStack[-1]
else: # if majorStack is empty, then finish
return
if popCount.get(majLast, -1) == -1:
popCount[majLast]=1
else:
popCount[majLast]=popCount[majLast]+1
# if last is a leaf, then find a path from the root to a leaf
if not list(T.successors(last)):
listoflists.append(copy.deepcopy(a_list))
a_list.pop()
find_all_paths()
print(listoflists)执行上述代码,所得之结果如下:
[['a', 'b', 'i'], ['a', 'b', 'f', 'h'], ['a', 'b', 'f', 'g'], ['a', 'b', 'c', 'd', 'e']]可见,我们的算法成功地找出了根节点到所有叶子结点的路径。
下面,我们想把问题拓展一下,假设要从一个有向图中找到从入口点到出口点的所有路径该怎么解决呢?注意,这里的有向图限定为无环的。例如,这里给出一个基于NetworkX生成的有向无环图范例:
G = nx.DiGraph()
G.add_node('a') #添加一个节点1
G.add_nodes_from(['b','c','d','e','f','g','i']) #加点集合
G.add_edges_from([('a','b'),('b','c'),('c','d'),('d','e')])
G.add_edges_from([('b','f'),('f','g'),('f','h'),('b','j')])
G.add_edges_from([('h','k'),('h','i'),('j','h'),('k','l')])
nx.draw(G, with_labels=True)
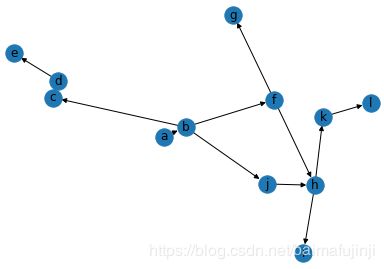
plt.show()执行上述代码,所得之结果如下图所示。可见从入口结点a到出口结点e、g、i、l的路径有[a->b->c->d->e]、[a->b->f->g]、[a->b->f->h->i]、[a->b->f->h->k->l]、[a->b->j->h->i]、[a->b->j->h->k->l]。
基于上面给出的在树中搜索路径的算法,于有向无环图中实现类似的功能其实是非常简单的,我们只要添加一行代码即可:
majorStack = deque([])
minorStack = deque([])
listoflists = []
a_list = []
entry_node = 'a'
def find_all_paths():
max_times = 0
minorStack.append(entry_node)
popCount = {}
while minorStack:
minLast = minorStack.pop()
majorStack.append(minLast)
a_list.append(minLast)
current_s_nodes = list(G.successors(minLast))
if current_s_nodes:
for element in current_s_nodes:
minorStack.append(element)
popCount[element]= -1
majLast = majorStack[-1]
#Loop condition:tos is a leaf OR all children of tos have been accessed
while( not list(G.successors(majLast)) or
( popCount.get(majLast, -1) == len(list(G.successors(majLast))))):
last = majorStack.pop()
if majorStack:
majLast = majorStack[-1]
else: # if majorStack is empty, then finish
return
if popCount.get(majLast, -1) == -1:
popCount[majLast]=1
else:
popCount[majLast]=popCount[majLast]+1
# if last is a leaf, then find a path from the root to a leaf
if not list(G.successors(last)):
listoflists.append(copy.deepcopy(a_list))
a_list.pop()
find_all_paths()
print(listoflists)执行上述代码,所得之结果如下:
[['a', 'b', 'j', 'h', 'i'], ['a', 'b', 'j', 'h', 'k', 'l'], ['a', 'b', 'f', 'h', 'i'], ['a', 'b', 'f', 'h', 'k', 'l'], ['a', 'b', 'f', 'g'], ['a', 'b', 'c', 'd', 'e']]可见所得之结果跟我们预想的是一致的。
【本文完】