算法高级（35）-最优路径选择-导航软件是怎么选择最佳路线的？

前面我们学习了图算法中的最短路径算法，可以参考我的这篇博文常用的图算法：最短路径(Shortest Path)，解决最短路的问题有以下算法，Dijkstra算法，Bellman-Ford算法，Floyd算法和SPFA算法等。简单回顾如下：

1. Dijkstra最短路径算法是基于递推的思想设计的未达顶点的最短路径一定是由已达顶点的最短路径求出。
2. Floyd最短路径算法只是Dijkstra最短路径算法的加强，其本质还是递推。
3. Dijkstra求单源、无负权的最短路。时效性较好，时间复杂度为O（V*V+E）。
4. Floyd求多源、无负权边的最短路。用矩阵记录图。时效性较差，时间复杂度O(V^3)。
5. Bellman-Ford求单源最短路，可以判断有无负权回路（若有，则不存在最短路），时效性较好，时间复杂度O（VE）。
6. SPFA是Bellman-Ford的队列优化，时效性相对好，时间复杂度O（kE）。（k<

Dijkstra算法能解决的是最短路径问题，今天我们再学习一下A*算法，看如何实现路径规划。

一、路径规划

路径规划是指导航软件或机器人的最优路径规划问题，即依据某个或某些优化准则（如工作代价最小、行走路径最短、行走时间最短等），在工作空间中找到一个从起始状态到目标状态能避开障碍物的最优路径。应注意以下几点：

1. 明确起始位置及终点
2. 避开障碍物
3. 尽可能做到路径上的优化
4. 成本最低

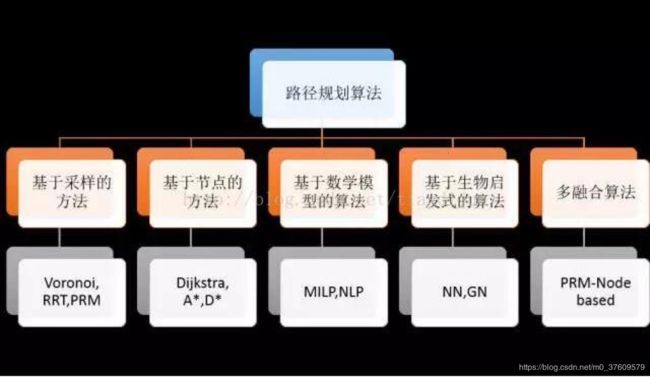
路径规划应用场景极丰富，最常见如游戏中NPC及控制角色的位置移动，百度地图等导航问题，小到家庭扫地机器人、无人机，大到各公司正争相开拓的无人驾驶汽车等。目前路径规划算法可以参考下图所示：

二、A*算法

导航引擎在得到目的地与自身位置信息后，就需要根据地图，计算出最优的路径，在导航中，经常提到的就是A*和Dijkstra算法。

A*算法，A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近，最终搜索速度越快。A*算法是导航路径计算中的标准算法。

A*算法作为Dijkstra算法的扩展，因其高效性而被广泛应用于寻路及图的遍历，如星际争霸等游戏中就大量使用。它比Dijkstra算法多了一个估算函数，若估算函数为0，A*算法也就退化为Dijkstra算法。A*算法是启发式搜索，是一种尽可能基于现有信息的搜索策略，也就是说搜索过程中尽量利用目前已知的诸如迭代步数，以及从初始状态和当前状态到目标状态估计所需的费用等信息。

Dijkstra和A*算法的效果演示动画：

A*算法可以选择下一个被检查的节点时引入了已知的全局信息，对当前结点距离终点的距离作出估计，作为评价该节点处于最优路线上的可能性的量度，这样可以首先搜索可能性大的节点，从而提高了搜索过程的效率。

A*算法的基本思想如下：引入当前节点j的估计函数f*,当前节点j的估计函数定义为：

                            f*(j)= g(j)+h*(j)

其中g(j)是从起点到当前节点j的实际费用的量度，h*(j)是从节点j到终点的最小费用的估计，可以依据实际情况，选择h*(j)的具体形式，h*(j)要满足一个要求：不能高于节点j到终点的实际最小费用。从起始节点点向目的节点搜索时，每次都搜索f*(j)最小的节点，直到发现目的节点。

A*算法的核心是设计估价函数，比较常见的为欧几里德距离和曼哈顿距离距离。

三、A*算法中的几个概念

1. 搜索区域（The Search Area）：图中的搜索区域被划分为了简单的二维数组，数组每个元素对应一个小方格，当然我们也可以将区域等分成是五角星，矩形等，通常将一个单位的中心点称之为搜索区域节点（Node），而非方格（Squares）。
2. 开放列表(Open List)：我们将路径规划过程中待检测的节点存放于Open List中，而已检测过的格子则存放于Close List中。
3. 父节点（parent）：在路径规划中用于回溯的节点，开发时可考虑为双向链表结构中的父结点指针。
4. 路径排序（Path Sorting）：具体往哪个节点移动由以下公式确定：F(n) = G(n) + H(n)G代表的是从初始位置A沿着已生成的路径到指定待检测格子的移动开销。H指定待测格子到目标节点B的估计移动开销。
5. 启发函数（Heuristics Function）：H为启发函数，也被认为是一种试探，由于在找到唯一路径前，我们不确定在前面会出现什么障碍物，因此用了一种计算H的算法，具体根据实际场景决定。在我们简化的模型中，H采用的是传统的曼哈顿距离（Manhattan Distance），也就是横纵向走的距离之和。

四、A*算法的实现流程

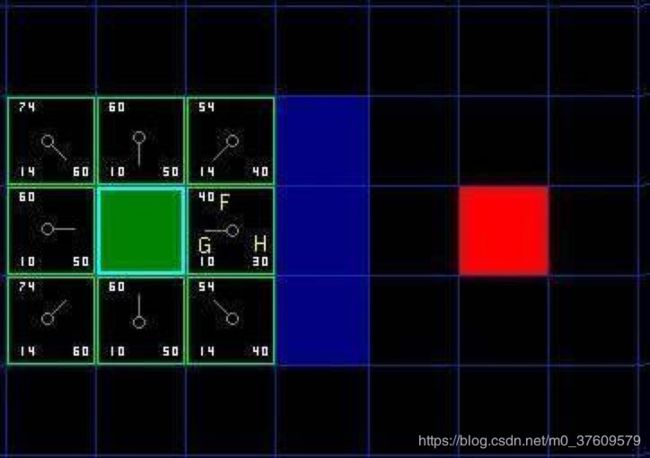
我们假设某人要从 A 点移动到 B 点，但是这两点之间被一堵墙隔开。如图所示，绿色是 A ，红色是 B ，中间蓝色是墙。

1.简化搜索区域(The Search Area)

简化为一个二维数组，每个方格的边长为10，即垂直水平方向移动开销为10。节点对角线为10，因此斜对角移动开销约等于14。

2.开始搜索(Starting the Search)

一旦我们把搜寻区域简化为一组可以量化的节点后，下一步要做的便是查找最短路径。在 A* 中，我们从起点开始，检查其相邻的方格，然后向四周扩展，直至找到目标。

将A点加入到Open List中，图中所示，上下左右移动一格距离为10，斜对角移动距离为14。环绕绿色方块的就是待检测格子，左下角的值就是G值，右下角为H值，左上角对应的就是F值，找到F值最小的节点作为新的起始位置。

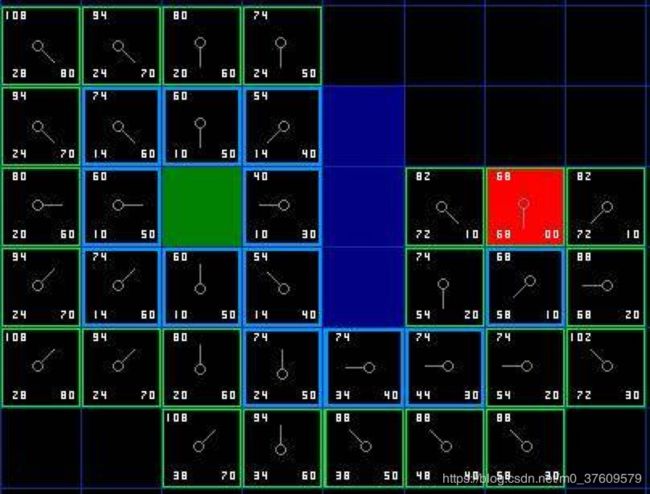
3.继续搜索(Continuing the Search)

 

绿色格子右侧的节点F为40，选作当前处理节点，并将这个点从Open List删除，增加到Close List中，对这个节点周围的8个格子进行判断，若是不可通过或已经在Close List中，则忽略之。否则执行以下步骤：

• 若当前处理格子的相邻格子已经在Open List中，那就计算临近节点经当前处理节点到起点的距离G是否比原G值小，若小，则把相邻节点的父节点（parent）设置为当前处理节点。
• 若当前处理格子的相邻格子不在Open List中，那么把它加入，并将它的父节点设置为该节点。

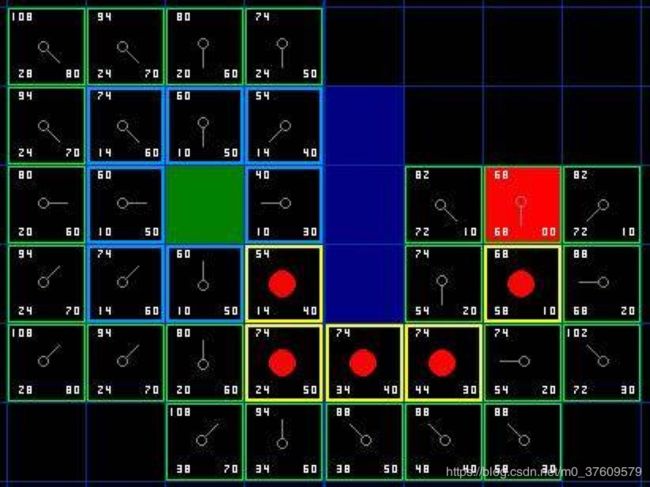
重复前面的步骤，直到终点B加入到了Open List中，再沿着各节点的父节点回溯遍历，将遍历得到的节点坐标保存下来，所得的节点就是最短路径。最终效果如图所示：

那么我们怎么样去确定实际路径呢？很简单，从终点开始，按着箭头向父节点移动，这样你就被带回到了起点，这就是你的路径。如下图所示。从起点 A 移动到终点 B 就是简单从路径上的一个方格的中心移动到另一个方格的中心，直至目标。就是这么简单！

五、A*算法总结

1. 把起点加入 open list 。
2. 重复如下过程：

   1. 遍历 open list ，查找 F 值最小的节点，把它作为当前要处理的节点。

   2. 把这个节点移到 close list 。

   3. 对当前方格的 8 个相邻方格的每一个方格？

      1. 如果它是不可抵达的或者它在 close list 中，忽略它。否则，做如下操作。

      2. 如果它不在 open list 中，把它加入 open list ，并且把当前方格设置为它的父亲，记录该方格的 F ， G 和 H 值。

      3. 如果它已经在 open list 中，检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好，用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样，把它的父亲设置为当前方格，并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话，改变后你可能需要重新排序。

   4. 停止，当你

      • 把终点加入到了 open list 中，此时路径已经找到了，或者

      •  查找终点失败，并且 open list 是空的，此时没有路径。

3. 保存路径。从终点开始，每个方格沿着父节点移动直至起点，这就是你的路径。

六、蚁群算法 

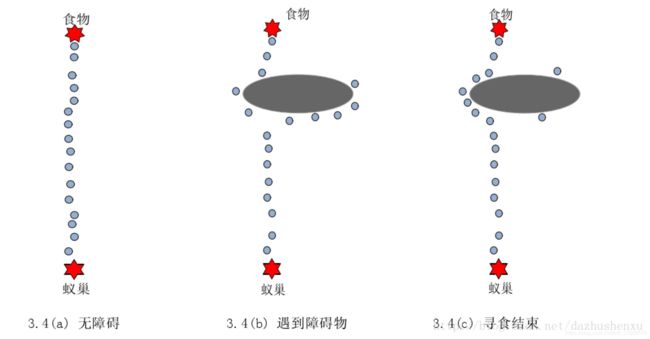
蚁群算法ACO：根据环境中各条路径的残留信息素的量来决定下一步的搜索方向。 可应用于无人机的路径规划。
蚂蚁运动的过程简单归纳为： 
1、当周围没有信息素指引时，蚂蚁的运动具有一定的惯性，并有一定的概率选择其他方向。
2、当周围有信息素的指引时，按照信息素的浓度强度概率性的选择运动方向。
3、找食物时，蚂蚁留下家相关的A信息素，找家时，蚂蚁留下食物相关的B信息素，并随着移动距离的增加，洒播的信息素越来越少。
4、随着时间推移，信息素会自行挥发。

一个简单的例子，如果现在有两条通往食物的路径，一条较长路径A,一条较短路径B,虽然刚开始A,B路径上都有蚂蚁，又因为B比A短，蚂蚁通过B花费的时间较短，随着时间的推移和信息素的挥发，逐渐的B上的信息素浓度会强于A，这时候因为B的浓度比A强，越来越多多蚂蚁会选择B，而这时候B上的浓度只会越来越强。如果蚂蚁一开始只在A上呢，注意蚂蚁的移动具有一定小概率的随机性，所以当一部分蚂蚁找到B时，随着时间的推移，蚂蚁会收敛到B上，从而可以跳出局部最优。 

七、总结

A*算法计算路径中一些改进的方法。

1. 应用地图数据分层的思想，简化地图中道路的网络结构，也能提高路径规划的性能。
2. 起始点与目的地的方向考虑进去，扩展时，有方向性进行扩展，可以大大减少计算量和存储空间。
3. 保存曾经的规划记录，也能达到快速检索的能力。Google的地图规划好像就采用的这种思想。

一些扩展的使用场景：

1. 无人机在不确定环境下自主运动的路径规划
2. 人工鱼群算法
3. 水下机器人路径规划

---

我的微信公众号：架构真经（关注领取免费资源）

参考文章

1. https://blog.csdn.net/iteye_5392/article/details/82309597
2. https://blog.csdn.net/dazhushenxu/article/details/77833023
3. https://blog.csdn.net/tiandijun/article/details/62226163
4. https://blog.csdn.net/autonavi2012/article/details/80923431
5. https://blog.csdn.net/hitwhylz/article/details/23089415
6. https://blog.csdn.net/Changer_sun/article/details/79078848
7. https://blog.csdn.net/viewcode/article/details/7925987