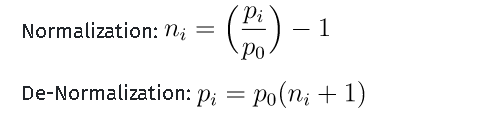LSTM股票预测
使用 Keras 和 Tensorflow 对时间序列数据的预测【对应Python版本为3.5.x 】,特别是在股市数据集上提供股票价格的动量指标。完整的代码可以查看这里 ,其中要求的版本信息在 requirements.txt文件中,由于版本不同可能会报错。接下来简单回顾下LSTM 单元,并用LSTM预测随机时间序列的正弦波 sine wave 。
LSTM NEURONS
传统的神经网络不能够解释依赖于信息和上下文的输入序列, 信息可以是句子中的先前出现的单词,用以允许上下文预测下一个单词可能是什么,或者它可以是序列的时间信息,它将允许该序列的基于时间的元素的上下文。简而言之,传统的神经网络中,各输入是独立的( stand-alone data vector )并且没有记忆的概念。RNN有梯度消失的问题(Vanishing Gradient Problem),而LSTM通过神经元在其管道中保持记忆的上下文,解决了序列和时间问题,因此不存在影响性能的梯度消失问题。
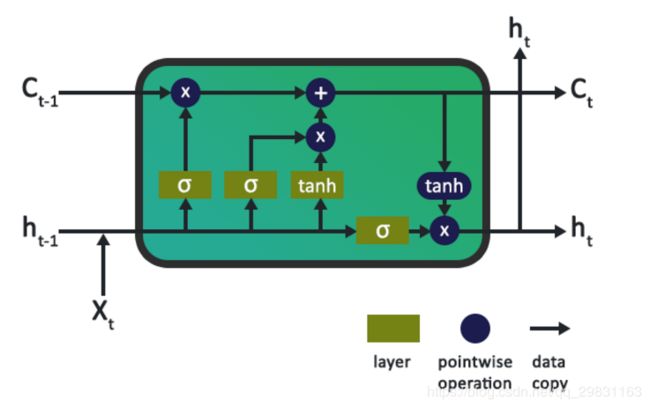
下图是LSTM neuron的内部原理图,其中它包括对数据的输入、输出和遗忘 起到门控作用的逐点操作【pointwise operations】,它作为单元状态【 cell state】的输入,单元状态中保留了网络和输入的长期记忆和上下文信息。
一个简单的例子:正弦波
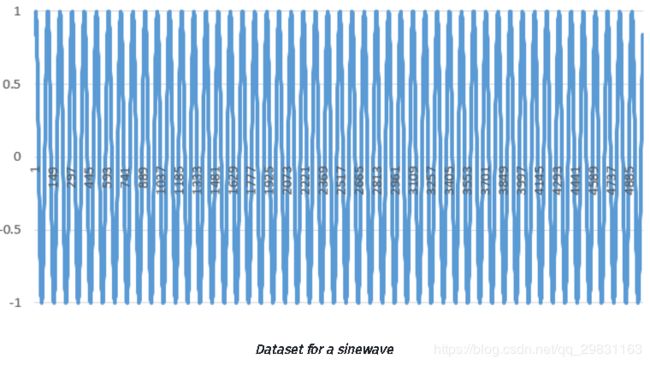
先创建需要的数据,再对函数的震荡( oscillations)建模,模型需要的数据在sinewave.csv 文件中,数据包含5001个数据点的时间段、振幅amplitude 和频率frequency为1的正弦波(角频率为6.28),时间差【时间增量】为0.01。数据可视化的结果如下所示:
有了数据之后,如何实现模型的建立呢?在设定了数据的窗口大小后,我们仅希望LSTM能学到正弦波并预测该序列接下来N步的正弦波形。先把 CSV 文件格式的数据转换并加载到 pandas 数据框【dataframe】,它输出numpy array 格式的数据,用来作为LSTM网络的输入。 Keras 中的LSTM 层接收3维(N,W,F)的numpy array ,其中N是训练序列的数目,W是序列长度,F是每个序列的特征数目。我选择的一个序列长度(读取的窗口大小)为50,这可以让网络在每个序列中知道正弦波的形状,从而教会自身基于先前窗口信息来建立序列的模式。序列本身是滑动的窗口,因此每次滚动1长度后,会保持与先前窗口的恒定重叠。一个长度为50的训练窗口的图形如下:
创建一个 DataLoader的类 class 来加载数据,为数据加载层提供概括信息。能注意到,在初始化DataLoader对象时,传入文件名,以及确定用于训练与测试的数据百分比的分割变量,以及允许选择选择一列或多列数据来进行单维或多维分析的列变量。
class DataLoader():
def __init__(self, filename, split, cols):
dataframe = pd.read_csv(filename)
i_split = int(len(dataframe) * split)
self.data_train = dataframe.get(cols).values[:i_split]
self.data_test = dataframe.get(cols).values[i_split:]
self.len_train = len(self.data_train)
self.len_test = len(self.data_test)
self.len_train_windows = None
def get_train_data(self, seq_len, normalise):
data_x = []
data_y = []
for i in range(self.len_train - seq_len):
x, y = self._next_window(i, seq_len, normalise)
data_x.append(x)
data_y.append(y)
return np.array(data_x), np.array(data_y)有了一个用于加载数据的数据对象后,就要构建深度神经网络模型。 再次为了概括信息,在给定存储在配置文件中的所需架构和超参数的情况下,我们的代码框架使用Model类和config.json文件来轻松构建模型的实例。 构建网络的主函数是build_model()函数,它接收解析的配置文件。此函数代码如下所示,它可以轻松扩展到更复杂的架构上。
class Model():
def __init__(self):
self.model = Sequential()
def build_model(self, configs):
timer = Timer()
timer.start()
for layer in configs['model']['layers']:
neurons = layer['neurons'] if 'neurons' in layer else None
dropout_rate = layer['rate'] if 'rate' in layer else None
activation = layer['activation'] if 'activation' in layer else None
return_seq = layer['return_seq'] if 'return_seq' in layer else None
input_timesteps = layer['input_timesteps'] if 'input_timesteps' in layer else None
input_dim = layer['input_dim'] if 'input_dim' in layer else None
if layer['type'] == 'dense':
self.model.add(Dense(neurons, activation=activation))
if layer['type'] == 'lstm':
self.model.add(LSTM(neurons, input_shape=(input_timesteps, input_dim), return_sequences=return_seq))
if layer['type'] == 'dropout':
self.model.add(Dropout(dropout_rate))
self.model.compile(loss=configs['model']['loss'], optimizer=configs['model']['optimizer'])
print('[Model] Model Compiled')
timer.stop()
加载数据并建立模型后,现在继续用训练数据训练模型。 为此,我们创建了一个单独的运行模块,它将Model和DataLoader 抽象出来的信息组合起来并用于训练、输出和可视化。
下面是训练我们模型的一般运行线程代码【 general run thread code 】。
configs = json.load(open('config.json', 'r'))
data = DataLoader(
os.path.join('data', configs['data']['filename']),
configs['data']['train_test_split'],
configs['data']['columns']
)
model = Model()
model.build_model(configs)
x, y = data.get_train_data(
seq_len = configs['data']['sequence_length'],
normalise = configs['data']['normalise']
)
model.train(
x,
y,
epochs = configs['training']['epochs'],
batch_size = configs['training']['batch_size']
)
x_test, y_test = data.get_test_data(
seq_len = configs['data']['sequence_length'],
normalise = configs['data']['normalise']
)
逐点预测
对于输出进行两种类型的预测:第一种将以逐点方式进行预测,即我们每次仅预测单个点,将此点绘制为预测,然后沿着下一个窗口进行预测,并再次使用完整的测试数据预测下一个点。
def predict_point_by_point(self, data):
#Predict each timestep given the last sequence of true data, in effect only predicting 1 step ahead each time
predicted = self.model.predict(data)
predicted = np.reshape(predicted, (predicted.size,))
return predicted
def predict_sequence_full(self, data, window_size):
#Shift the window by 1 new prediction each time, re-run predictions on new window
curr_frame = data[0]
predicted = []
for i in range(len(data)):
predicted.append(self.model.predict(curr_frame[newaxis,:,:])[0,0])
curr_frame = curr_frame[1:]
curr_frame = np.insert(curr_frame, [window_size-2], predicted[-1], axis=0)
return predicted
predictions_pointbypoint = model.predict_point_by_point(x_test)
plot_results(predictions_pointbypoint, y_test)
predictions_fullseq = model.predict_sequence_full(x_test, configs['data']['sequence_length'])
plot_results(predictions_fullseq, y_test)
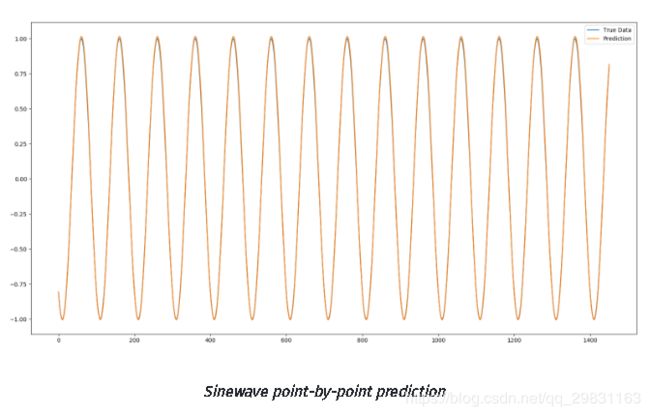
逐点预测的正弦波形图如下:
完整的序列预测
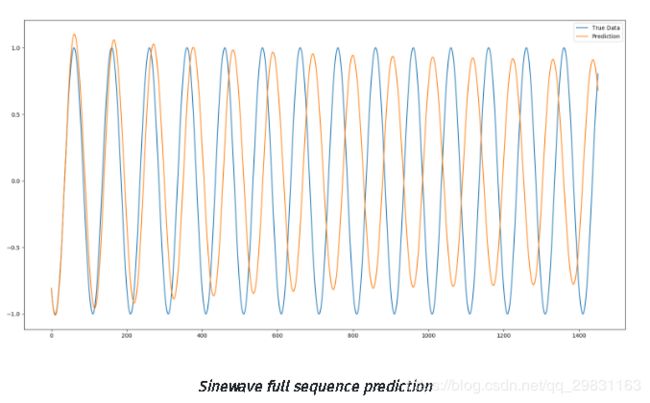
对完整的序列预测的正弦波形如下图所示。
sinewave这个 例子所使用的网络结构和 超参数,可以参考下方的config file.文件
{
"data": {
"filename": "sinewave.csv",
"columns": [
"sinewave"
],
"sequence_length": 50,
"train_test_split": 0.8,
"normalise": false
},
"training": {
"epochs": 2,
"batch_size": 32
},
"model": {
"loss": "mse",
"optimizer": "adam",
"layers": [
{
"type": "lstm",
"neurons": 50,
"input_timesteps": 49,
"input_dim": 1,
"return_seq": true
},
{
"type": "dropout",
"rate": 0.05
},
{
"type": "lstm",
"neurons": 100,
"return_seq": false
},
{
"type": "dropout",
"rate": 0.05
},
{
"type": "dense",
"neurons": 1,
"activation": "linear"
}
]
}
}图形上的正弦波形覆盖了真实数据,可以看出 仅仅1个 epoch 和一个相当小的训练数据集,深度LSTM网络就已经能很好地预测正弦函数。随着预测的时期越来越长,误差幅度【error margin 】也随之增加,因为在预测未来的数据时,先前的误差会被逐渐放大。
sin函数是一个非常简单的具有零噪声的震荡函数,增加训练的 epochs 并拿掉 dropout 层会容易过拟合, 对测试数据也是一样。但对于其它真实数据的例子,模型在训练集上过拟合会导致模型的测试精度直线下降,泛化性能差。
接下来看看这个模型在其它真实数据上的效果。
没那么简单的股市预测
股票市场时间序列不是任何可以映射的特定静态函数。 描述股票市场时间序列运动的最佳属性是随机游走。 作为随机过程,真正的随机游走没有可预测的模式,因此尝试对其进行建模将毫无意义。 幸运的是,许多方面都在持续争论说股票市场不是一个纯粹的随机过程,这使我们能够理解时间序列可能具有某种隐藏模式。 正是这些隐藏的模式,LSTM深度网络是预测的主要候选者。
使用数据文件夹中的sp500.csv文件,它包含2000年1月至2018年9月标准普尔500股票指数【 Equity Index 】的开盘价,最高价,最低价,收盘价以及每日交易量。
第一个例子是仅使用Close price这一列创建一维模型。 调整config.json文件以反映新数据,保持大部分参数相同。 然而,需要做出的一个改变是,与仅具有介于-1到+1之间的数值范围的正弦波不同,收盘价是股票市场不断变化的绝对价格。 这意味着如果不对数据进行标准化处理,它就永远不会收敛。为了解决这个问题,我们将采用每个n大小的训练/测试数据窗口并对每个窗口进行标准化以反映从该窗口开始的百分比变化(因此点i = 0处的数据将始终为0)。 我们将使用以下等式进行归一化,然后在预测过程结束时进行去标准化【De-normalization】,以获得预测中的真实数据:
n = 价格变化的标准化列表[窗口] 【】
p = 调整后的每日收益价格的原始列表 【 raw list [window] of adjusted daily return prices 】
把 normalise_windows() 函数添加到 DataLoader 类中来实现数据变换, 在 config file 文件中包含一个Boolean normalise flag 【布尔标准化标志位】用来denote这些窗口的标准化
def normalise_windows(self, window_data, single_window=False):
'''Normalise window with a base value of zero'''
normalised_data = []
window_data = [window_data] if single_window else window_data
for window in window_data:
normalised_window = []
for col_i in range(window.shape[1]):
normalised_col = [((float(p) / float(window[0, col_i])) - 1) for p in window[:, col_i]]
normalised_window.append(normalised_col)
# reshape and transpose array back into original multidimensional format
normalised_window = np.array(normalised_window).T
normalised_data.append(normalised_window)
return np.array(normalised_data)
窗口标准化了之后,可以像在sinewave数据上那样运行模型,但要做一个重要的改变:不使用framework中的 model.train()方法,而使用创建的model.train_generator() 方法,这么做是因为我们发现,训练大型数据集时很容易耗尽内存,当model.train()函数将整个数据集加载到内存中,然后对内存中的每个窗口标准化时,容易导致内存溢出。相反,我们使用了Keras的fit_generator()函数,允许使用python生成器动态训练数据集来绘制数据,这意味着内存利用率将大大降低。 下面的代码详细说明了用于运行三种类型预测的新运行线程(逐点,完整序列和多序列)。
configs = json.load(open('config.json', 'r'))
data = DataLoader(
os.path.join('data', configs['data']['filename']),
configs['data']['train_test_split'],
configs['data']['columns']
)
model = Model()
model.build_model(configs)
x, y = data.get_train_data(
seq_len = configs['data']['sequence_length'],
normalise = configs['data']['normalise']
)
# out-of memory generative training
steps_per_epoch = math.ceil((data.len_train - configs['data']['sequence_length']) / configs['training']['batch_size'])
model.train_generator(
data_gen = data.generate_train_batch(
seq_len = configs['data']['sequence_length'],
batch_size = configs['training']['batch_size'],
normalise = configs['data']['normalise']
),
epochs = configs['training']['epochs'],
batch_size = configs['training']['batch_size'],
steps_per_epoch = steps_per_epoch
)
x_test, y_test = data.get_test_data(
seq_len = configs['data']['sequence_length'],
normalise = configs['data']['normalise']
)
predictions_multiseq = model.predict_sequences_multiple(x_test, configs['data']['sequence_length'], configs['data']['sequence_length'])
predictions_fullseq = model.predict_sequence_full(x_test, configs['data']['sequence_length'])
predictions_pointbypoint = model.predict_point_by_point(x_test)
plot_results_multiple(predictions_multiseq, y_test, configs['data']['sequence_length'])
plot_results(predictions_fullseq, y_test)
plot_results(predictions_pointbypoint, y_test){
"data": {
"filename": "sp500.csv",
"columns": [
"Close"
],
"sequence_length": 50,
"train_test_split": 0.85,
"normalise": true
},
"training": {
"epochs": 1,
"batch_size": 32
},
"model": {
"loss": "mse",
"optimizer": "adam",
"layers": [
{
"type": "lstm",
"neurons": 100,
"input_timesteps": 49,
"input_dim": 1,
"return_seq": true
},
{
"type": "dropout",
"rate": 0.2
},
{
"type": "lstm",
"neurons": 100,
"return_seq": true
},
{
"type": "lstm",
"neurons": 100,
"return_seq": false
},
{
"type": "dropout",
"rate": 0.2
},
{
"type": "dense",
"neurons": 1,
"activation": "linear"
}
]
}
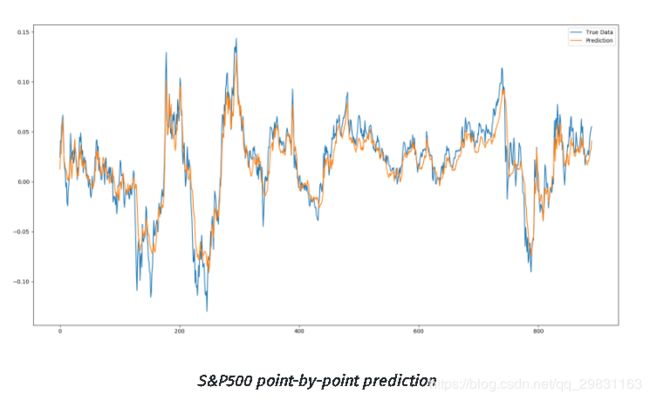
}如上所述,在单个逐点预测上运行数据可以非常接近地匹配收益的效果。 但这有点欺骗性。 经过仔细检查,预测线由奇异的预测点组成,这些预测点在它们后面具有整个先前的真实历史窗口。 因此,网络不需要了解时间序列本身,除了每个下一个点很可能不会离最后一点太远。 因此,即使它得到错误点的预测,下一个预测也会考虑真实历史并忽略不正确的预测,但又会允许发生错误。一个重要的用途是,虽然它不知道确切的下一个价格是多少,但它确实能够准确地表示下一个价格的范围。此信息可用于波动率预测等(能够预测市场中高波动率或低波动率的时段对于特定交易策略可能非常有利),还可用于异常检测的良好指标。异常检测可以通过预测下一个点,然后将其与真实数据进行比较来实现,如果真实数据值与预测点明显不同,则可以将该数据点进行异常标记。
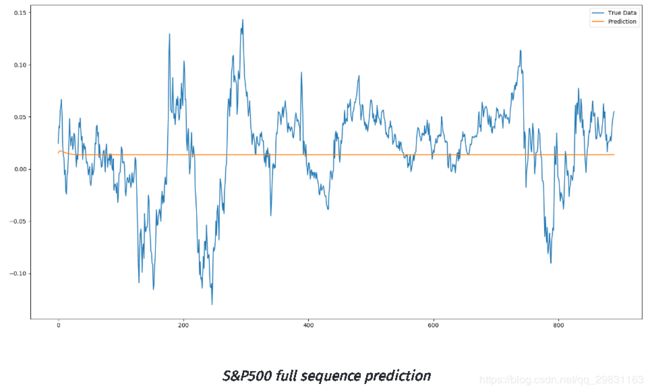
full sequence prediction
全序列预测至少可以说是这个超参数的训练模型中最没用的预测,但我们可以快速发现,最优的模式是收敛到时间序列的某个均衡,平均回归交易者可能会在那个阶段宣称,该模型只是找到价格序列在波动率被消除时将恢复的平均值。
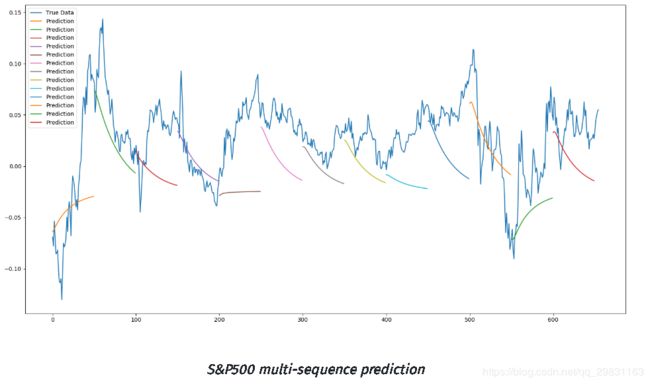
多序列预测
最后,我们对该模型进行了第三种预测,我将其称为多序列预测。 这是完整序列预测的混合,因为它仍然使用测试数据初始化测试窗口,预测下一个点,然后使用下一个点创建一个新窗口。但是,一旦输入窗口完全由过去的预测组成,它就会停止,向前移动一个完整的窗口长度,用真实的测试数据重置窗口,然后再次启动该过程。 实质上,这给出了对测试数据的多个趋势线预测,以便能够分析模型能够获得未来动量趋势的程度。
从多序列预测中可以发现,,网络正确预测了绝大多数时间序列的趋势(和趋势的幅度)。虽然不完美,但它确实表明了LSTM深度神经网络在顺序【sequential 】和时间序列问题中的有用性。 通过仔细调整超参数,肯定可以使精度更高。
多维LSTM 预测
到目前为止,我们的模型仅采用一维输入(用S&P500数据集时的“收盘”价)。 但是对于更复杂的数据集,序列自然存在许多不同的维度,可用于增强数据集,从而提高模型的准确性。对于我们的S&P500数据集,我们可以看到我们有五个可能的维度,包括开盘,最高,最低,收盘和交易量。 我们开发的框架允许使用多维输入数据集,因此我们需要做的就是编辑这些列并适当地设置第一层的input_dim值,以运行我们的模型。 此处我将使用两个维度运行模型; “收盘”和“成交量”。
{
"data": {
"filename": "sp500.csv",
"columns": [
"Close",
"Volume"
],
"sequence_length": 50,
"train_test_split": 0.85,
"normalise": true
},
"training": {
"epochs": 1,
"batch_size": 32
},
"model": {
"loss": "mse",
"optimizer": "adam",
"layers": [
{
"type": "lstm",
"neurons": 100,
"input_timesteps": 49,
"input_dim": 2,
"return_seq": true
},
{
"type": "dropout",
"rate": 0.2
},
{
"type": "lstm",
"neurons": 100,
"return_seq": true
},
{
"type": "lstm",
"neurons": 100,
"return_seq": false
},
{
"type": "dropout",
"rate": 0.2
},
{
"type": "dense",
"neurons": 1,
"activation": "linear"
}
]
}
}
使用多维(收盘和成交量)多序列预测的可视化 结果如下图所示;
我们可以看到随着在【收盘】的基础上再添加第二个维度【成交量】后,输出预测变得更加细化。 预测趋势线似乎更准确地预测即将到来的小幅下跌【dips】,不仅是从一开始的主流趋势,趋势线的准确性似乎也在这种特殊情况下得到改善。
结论
LSTM已成功应用于众多现实问题,从此处所述的经典时间序列问题到文本自动纠正,异常检测和欺诈检测,以及正在开发的自动驾驶汽车技术的核心。目前使用上述vanilla LSTM仍 存在一些局限性,特别是在使用金融时间序列时,该系列本身具有很难建模的非平稳特性(尽管使用贝叶斯深度神经网络方法已经取得了进展) 解决时间序列的非平稳性)。 同样对于一些应用,还发现基于注意力的神经网络机制的新进展已经超过LSTM(并且LSTM与这些基于注意力的机制相结合已经超出了它们自身)。
然而,截至目前,LSTM在更经典的统计时间序列方法上提供了显着的进步,能够非线性地建模关系并且能够以非线性方式处理具有多个维度的数据。
注:本文简单地翻译了这篇英文文章, 开发的框架的完整源代码可以在GitHub上找到 :
参考资料:通过LSTM神经网络预测股市-云栖社区-阿里云