实现对于n阶行列式的计算

实现对于n阶行列式的计算，对于行列式的计算是对于我们的实际有着很大的帮助的。例如我们在现实生活中遇到一个问题，它抽象成一个数学模型或事一个n元1次方程组，现在求解问题。这类问题有很多。这就要借助我们的线形代数的知识来求解。先实现行列式的求解问题：

                行列式的公式为：Sum=∑ (-1)^t*a1p1*a2p2*...*anpn   （这里的t表示排列p1 p2...pn 的逆序数）

这是线形代数的基础知识。我们利用该公式来求解：

实现的程序如下：

#include

#include

#include

struct node{

    int value;

    int size;

    int local;

};

/* 交换两个数据 */

void swap(int* a, int* b)

{

    int c = *a;

    *a = *b;

    *b = c;

}

/*

 *计算n阶行列式中的每一个行列式的值，sum就是计算行列式的最终结果

 */

void print_order_Counters(double **a,int * arr,int size,double *sum)

{

    struct node * pstr=NULL;

    int count=0;

    pstr=(struct node *)calloc(size,sizeof(struct node));

    for(int i=0;i

    {

        pstr[i].value=arr[i];

        pstr[i].size=0;

        pstr[i].local=i;

    }

    for(int i=0;i

    {

        for(int j=pstr[i].local;j>=0;j--)

        {

            if(pstr[i].value

            {

                pstr[i].size++;

            }

        }

    }

    for(int i=0;i

    {

        count+=pstr[i].size;

    }

   // printf("the count is %d\t,-1^square is %f\n",count,pow(-1, count));

    //double temp=a[0][pstr[0].value]*a[1][pstr[1].value]*a[2][pstr[2].value];

    double temp=1;

    for(int i=0;i

        temp*=a[i][pstr[i].value];

    *sum+=temp*pow(-1, count);

   // printf("%f\n",temp);

    free(pstr);

}

void perm(int str[], int index, int str_size,double **arr,double * sum)

{

    int j = 0;

    if(index == str_size)

    {

        /*

        for(i = 0; i < str_size; i++)

        {

            printf("%d ",str[i]);

        }

        printf("\n");

         */

        print_order_Counters(arr,str,str_size,sum);

    }

    else

    {

        for(j = index;j < str_size; j++)

        {

            swap(&str[j],&str[index]);

            perm(str,index+1,str_size,arr,sum);

            swap(&str[j],&str[index]);

        }

    }

}

int main(int argv,const char * argc[])

{

    //计算n阶行列式

    int * index;

    double **arr=NULL;

    double sum=0;

    int n;

    fprintf(stdout, "行列式为:");

    fscanf(stdin, "%d",&n);

    index=new int[n];

    for(int i=0;i

        index[i]=i;

    arr=new double*[n];

    for(int i=0;i

    {

        arr[i]=new double[n];

        fprintf(stdout, "the %d colum is",i+1);

        for(int j=0;j

            scanf("%lf",&arr[i][j]);

    }

    perm(index, 0, n, arr, &sum);

    fprintf(stdout, "the determinant is\n");

    for(int i=0;i

    {

        for(int j=0;j

            fprintf(stdout, "%.02lf\t",arr[i][j]);

        fprintf(stdout, "\n");

    }

    printf("the result is :%.06f\n",sum);

    free(index);

    for(int i=0;i

        free(arr[i]);

    return 0;

}

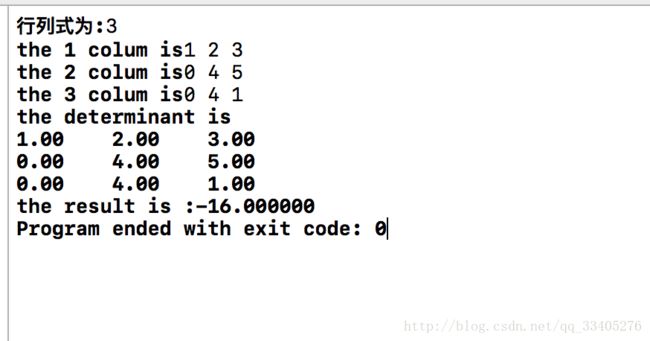
测试用例为：