【数据结构】图
1.存储结构:
- 邻接矩阵
- 邻接表
2.图的遍历:
- 深度优先遍历
- 广度优先遍历
3.算法实现:
定义图的抽象数据类型(ADT):
public interface IGraph{
public int getNumOfVertex(); //获取顶点的个数
boolean insertVex(E v); //插入顶点
boolean deleteVex(E v); //删除顶点
int indexOfVex(E v); //定位顶点的位置
E valueOfVex(int v); //定位指定位置的顶点
boolean insertEdge(int v1, int v2, int weight); //插入边
boolean deleteEdge(int v1, int v2); //删除边
public int getEdge(int v1, int v2); //查找边
String dfs(int v); //深度优先遍历
String bfs(int v); //广度优先遍历
}
邻接矩阵存储:
public class GraphAdjMatrix implements IGraph{
private E[] vexs; //存储图的顶点的一维数组
private int[][] edges; //存储图的边的二维数组
private int numOfVexs; //顶点的实际数量
private int maxNumOfVexs; //顶点的最大数量
private boolean[] visited; //判断顶点是否被访问过
@SuppressWarnings("unchecked")
public GraphAdjMatrix(int maxNumOfVexs, Class type) {
this.maxNumOfVexs = maxNumOfVexs;
edges = new int[maxNumOfVexs][maxNumOfVexs];
vexs = (E[]) Array.newInstance(type, maxNumOfVexs);
}
//得到顶点的数目
@Override
public int getNumOfVertex() {
return numOfVexs;
}
//插入顶点
@Override
public boolean insertVex(E v) {
if(numOfVexs >= maxNumOfVexs){
return false;
}
vexs[numOfVexs++] = v;
return true;
}
//删除顶点
@Override
public boolean deleteVex(E v) {
for(int i = 0; i < numOfVexs; i++){
if(vexs[i].equals(v)){
for(int j = i; j < numOfVexs - 1; j++){
vexs[j] = vexs[j + 1];
}
vexs[numOfVexs - 1] = null;
for (int col = i; col < numOfVexs - 1; col++){
for(int row = 0; row < numOfVexs; row++){
edges[col][row] = edges[col + 1][row];
}
}
for(int row = i; row < numOfVexs -1; row++){
for(int col = 0; col < numOfVexs; col++){
edges[col][row] = edges[col][row + 1];
}
}
numOfVexs--;
return true;
}
}
return false;
}
//定位顶点的位置
@Override
public int indexOfVex(E v) {
for (int i = 0; i < numOfVexs; i++){
if(vexs[i].equals(v)){
return i;
}
}
return -1;
}
//定位指定位置的顶点
@Override
public E valueOfVex(int v) {
if(v < 0 || v >= numOfVexs){
return null;
}
return vexs[v];
}
//插入边
@Override
public boolean insertEdge(int v1, int v2, int weight) {
if(v1 < 0 || v2 < 0 || v1 >= numOfVexs || v2 >= numOfVexs){
throw new ArrayIndexOutOfBoundsException();
}
edges[v1][v2] = weight;
edges[v2][v1] = weight;
return true;
}
//删除边
@Override
public boolean deleteEdge(int v1, int v2) {
if(v1 < 0 || v2 < 0 || v1 >= numOfVexs || v2 >= numOfVexs){
throw new ArrayIndexOutOfBoundsException();
}
edges[v1][v2] = 0;
edges[v2][v1] = 0;
return true;
}
//查找边
@Override
public int getEdge(int v1, int v2) {
if(v1 < 0 || v2 < 0 || v1 >= numOfVexs || v2 >= numOfVexs){
throw new ArrayIndexOutOfBoundsException();
}
return edges[v1][v2];
}
//深度优先遍历
@Override
public String dfs(int v) {
if(v < 0 || v > numOfVexs){
throw new ArrayIndexOutOfBoundsException();
}
visited = new boolean[numOfVexs];
StringBuilder sb = new StringBuilder();
Stack stack = new Stack<>();
stack.push(v);
visited[v] = true;
while (!stack.isEmpty()){
v = stack.pop();
sb.append(vexs[v] + ",");
for(int i = numOfVexs - 1; i >= 0; i--){
if((edges[v][i] != 0 && edges[v][i] != Integer.MAX_VALUE) && !visited[i]){
stack.push(i);
visited[i] = true;
}
}
}
return sb.length() > 0 ? sb.substring(0, sb.length() - 1) : null;
}
//广度优先搜素
@Override
public String bfs(int v) {
if (v < 0 || v >= numOfVexs){
throw new ArrayIndexOutOfBoundsException();
}
visited = new boolean[numOfVexs];
StringBuilder sb = new StringBuilder();
Queue queue = new LinkedList<>();
queue.offer(v);
visited[v] = true;
while (!queue.isEmpty()){
v = queue.poll();
sb.append(vexs[v] + ",");
for (int i = 0; i < numOfVexs; i++){
if((edges[v][i] != 0 && edges[v][i] != Integer.MAX_VALUE) && !visited[i]){
queue.offer(i);
visited[i] = true;
}
}
}
return sb.length() > 0 ? sb.substring(0, sb.length() - 1) : null;
}
}
测试类:
public class TestGraphAdjMatrix {
public static void main(String[] args) {
String[] vexs = {"v1", "v2", "v3", "v4", "v5", "v6"};
int[][] edges =
{ {0, 20, 0, 10, 0, 0},
{20, 0, 10, 0, 0, 35},
{0, 10, 0, 20, 25, 5},
{10, 0, 20, 0, 15, 0},
{0, 0, 25, 15, 0, 0},
{0, 35, 5, 0, 0, 0}
};
IGraph graph = new GraphAdjMatrix(10,String.class);
Scanner sc = new Scanner(System.in);
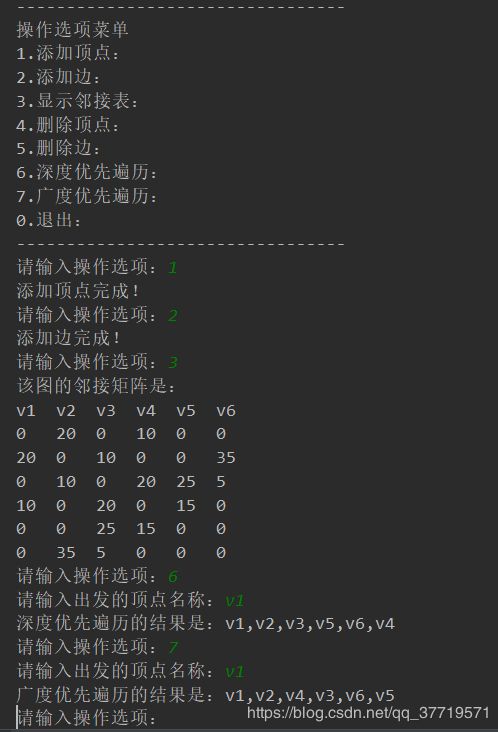
System.out.println("---------------------------------");
System.out.println("操作选项菜单");
System.out.println("1.添加顶点:");
System.out.println("2.添加边:");
System.out.println("3.显示邻接表:");
System.out.println("4.删除顶点:");
System.out.println("5.删除边:");
System.out.println("6.深度优先遍历:");
System.out.println("7.广度优先遍历:");
System.out.println("0.退出:");
System.out.println("---------------------------------");
char ch;
do{
System.out.print("请输入操作选项:");
ch = sc.next().charAt(0);
switch (ch){
case '1':
for (int i = 0; i < vexs.length; i++){
graph.insertVex(vexs[i]);
}
System.out.println("添加顶点完成!");
break;
case '2':
for (int i = 0; i < edges.length; i++) {
for (int j = i + 1; j < edges.length; j++) {
if (edges[i][j] != 0) {
graph.insertEdge(i, j, edges[i][j]);
}
}
}
System.out.println("添加边完成!");
break;
case '3':
int numOfVertex = graph.getNumOfVertex();
if(numOfVertex == 0){
System.out.println("图还没有创建!");
return;
}
System.out.println("该图的邻接矩阵是:");
for (int i = 0; i < numOfVertex; i++) {
System.out.print(graph.valueOfVex(i) + "\t");
}
System.out.println();
for (int i = 0; i < graph.getNumOfVertex(); i++){
for (int j = 0; j < graph.getNumOfVertex(); j++){
System.out.print(graph.getEdge(i, j) + "\t");
}
System.out.println("");
}
break;
case '4':
System.out.print("请输入要删除顶点的名称:");
String vex = sc.next();
graph.deleteVex(vex);
System.out.println(vex + "删除成功!");
break;
case '5':
System.out.print("请输入要删除边的第一个的顶点的名称:");
String vex1 = sc.next();
System.out.print("请输入要删除边的第二个的顶点的名称:");
String vex2 = sc.next();
graph.deleteEdge(graph.indexOfVex(vex1), graph.indexOfVex(vex2));
System.out.println(vex1 + "与" + vex2 + "之间的边被删除");
break;
case '6':
System.out.print("请输入出发的顶点名称:");
vex = sc.next();
String path = graph.dfs(graph.indexOfVex(vex));
System.out.print("深度优先遍历的结果是:");
System.out.println(path);
break;
case '7':
System.out.print("请输入出发的顶点名称:");
vex = sc.next();
String path1 = graph.bfs(graph.indexOfVex(vex));
System.out.print("广度优先遍历的结果是:");
System.out.println(path1);
break;
}
}while (ch != '0');
sc.close();
}
}
- 图的深度优先搜索使用压栈出栈操作实现
- 图的广度优先搜索可以使用队列实现
参考书目:数据结构(java版)