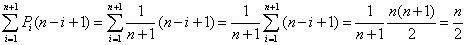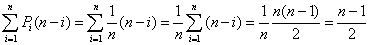线性表
- 一、定义与基本操作
- 二、线性表实现为顺序表
- 1、C 代码:
- 2、顺序表的定义
- 2.1、顺序表的存储空间的分配
- 2.2、顺序表的基本操作
- 1)增
- 2)删
- 3)改
- 4)查
- 5)取值与遍历输出
- 2.3、顺序表的排序
- 3、顺序表的优劣
- 三、顺序表的相关算法
- 2、顺序表翻转
- 3、全部删除指定值的元素
- 4、范围删除
- 5、去重
- 6、表合并
- 7、交换或插入
- 8、半域翻转
- 9、求A+B的中位数
- 10、求主元素
- 11、求最小正整数
一、定义与基本操作
1、线性表的定义
线性表是具有相同数据类型的 n 个数据元素的有限序列,n 即为表长。- n = 0 时,线性表是一个空表。
- 记线性表为 L,则
L=(a1,a2,a3,...,an),其中 a1 为第一个元素称为表头元素,an 为最后一个元素称为表尾元素;除表头元素外,线性表的每个元素有且仅有一个直接前驱,除表尾元素,每个元素有且只有一个直接后继。
- 根据线性表的定义,有如下特点:
1)有限个元素。
2)元素具有逻辑顺序,每个元素都有先后次序。
3)每个元素都是数据元素,且每个元素都是单个元素。
4)元素的数据类型一致,每个元素占据相同大小存储空间。
2、线性表的基本操作:
一个数据结构的基本操作是指其最核心、最基本的操作,其他操作都可以通过这些基本操作的有限次复合来完成。线性表的基本操作有增上改查、排序以及求表长、初始化线性表等。
1)create():构造一个空的线性表。
2)InitList():初始化线性表。
3)getLength():返回线性表表长。
4)getValue():返回指下标的值。
5)getIndex():返回指定值的下标。
6)add():线性表追加元素。
7)Insert():线性表插入元素。
8)Change():修改线性表指定下标元素。
9)DelValue():删除指定值的元素。
10)DelIndex():删除指定下标的元素。
11)Sort():排序元素。
12)Display():输出线性表元素。
13)Empty():判断线性表是否为空。
14)Destroy():销毁线性表。
二、线性表实现为顺序表
1、C 代码:
#pragma once
#include
using namespace std;
constexpr auto Initsize = 20;
typedef struct {
int* data;
int Maxsize, length;
}SeqList;
SeqList create(int maxsize = 20)
{
SeqList list;
list.data = new int[Initsize];
list.length = 20;
list.Maxsize = maxsize;
return list;
}
void initList(SeqList& list, int arr[], int len)
{
if (len <= list.length)
{
for (int i = 0; i < len; i++)
{
list.data[i] = arr[i];
}
list.length = len;
}
else
{
if (list.Maxsize >= len) {
delete[] list.data;
list.data = new int[len];
list.length = len;
for (int i = 0; i < len; i++)
{
list.data[i] = arr[i];
}
}
else
{
cout << "Error! The length of the arr is so long that the Maxsize of sqelist could not hold.";
}
}
}
void AddValue(SeqList& list, int value)
{
list.data[list.length] = value;
list.length += 1;
}
void InsertValue(SeqList& list, int value, int index)
{
if (index > list.length)
{
cout << "Error! the index is invaild!" << endl;;
return;
}
if (index == list.length)
AddValue(list, value);
else
{
for (int i = list.length; i >= index - 1; i--)
{
list.data[i] = list.data[i - 1];
}
list.data[index - 1] = value;
list.length += 1;
}
}
int getValue(SeqList list, int index)
{
if (index >= list.length)
return NAN;
return list.data[index - 1];
}
int getIndex(SeqList list, int value)
{
int i = 0;
for (i = 0; i < list.length; i++)
if (list.data[i] == value)
break;
if (i >= list.length)
return NAN;
return i + 1;
}
int getPreByValue(SeqList list, int value)
{
int cur = getIndex(list, value);
if (cur == 0)
{
cout << "The value is no exist!" << endl;
return NAN;
}
return list.data[cur - 2];
}
int getLastByVlue(SeqList list, int value)
{
int cur = getIndex(list, value);
if (cur == 0)
{
cout << "The value is no exist!" << endl;
return NAN;
}
return list.data[cur];
}
void change(SeqList& list, int index, int value)
{
if (index > list.length)
{
cout << "Error! the index is invaild!";
return;
}
list.data[index - 1] = value;
}
void delValue(SeqList& list, int value)
{
int cur = getIndex(list, value);
if (cur != 0)
{
for (int i = cur - 1; i < list.length - 1; i++)
list.data[i] = list.data[i + 1];
list.length -= 1;
}
else
cout << "What you want delete is no exist in this seqList!" << endl;
}
void delIndex(SeqList& list, int index)
{
if (index > list.length)
{
cout << "Error! The index is invalid!" << endl;
return;
}
for (int i = index - 1; i < list.length - 1; i++)
{
list.data[i] = list.data[i + 1];
}
list.length -= 1;
}
void AscSort(SeqList& list)
{
for (int i = 0; i < list.length; i++)
for (int j = i + 1; j < list.length; j++)
{
if (list.data[i] > list.data[j])
{
int temp = list.data[i];
list.data[i] = list.data[j];
list.data[j] = temp;
}
}
}
void DesSort(SeqList& list)
{
for (int i = 0; i < list.length; i++)
for (int j = i + 1; j < list.length; j++)
{
if (list.data[i] < list.data[j])
{
int temp = list.data[i];
list.data[i] = list.data[j];
list.data[j] = temp;
}
}
}
void display(SeqList list)
{
for (int i = 0; i < list.length; i++)
cout << list.data[i] << " ";
cout << endl;
}
bool empty(SeqList list)
{
if (list.length == 0)
return true;
return false;
}
void destroy(SeqList& list)
{
delete[] list.data;
list.length = 0;
list.Maxsize = 0;
}
2、顺序表的定义
顺序表指采用顺序存储结构进行实现的线性表。,即在内存中用一组连续的存储单元存储线性表中的数据元素,从而使逻辑上相邻的元素在物理位置上也相邻,即彪总的元素的逻辑顺序与物理顺序相同,这也是顺序表的特点。
2.1、顺序表的存储空间的分配
- 创建一个顺序表时,需要为其分配存储空间,有两种策略:
静态分配和动态分配。
- 采用静态分配时,需要实现知道所创建的顺序表的元素的个数,然后一次性将所用空间申请下来,如下:
ElemType data[size]。
- 采用静态分配的顺序表无法增加元素,在所申请空间已全部使用时;强行追加元素则会导致溢出,产生不可预测的后果。
- 采用动态分配时,不必一次性将全部空间申请下来,而是根据需要进行动态扩充,采用动态分配的顺序表关键语句如下:
ElemType *data
- 也就是声明为指针数组,在初始化时申请一个适当大小的存储空间,语句如下:
list.data = new ElemType[initsize];
2.2、顺序表的基本操作
- 顺序表的基本操作有
增删改查与遍历,这是所有顺序表的其他诸如排序等操作的基础。
1)增
- 指向已创建且初始化的线性表中增加元素,有两种方式:
追加和插入。
- 元素追加是在顺序表末尾增加元素,插入元素则在序列中间增加,
最显著的区别就是追加元素不影响已有元素的下标,而插入则会影响插入位置之后的元素的下标。
- 所以二者的时间复杂度是完全不一样的,追加元素的时间复杂度时常数阶,而插入元素的时间复杂度与顺序表规模和所插入的位置有关,最好的时候只需移动一个元素,即插入在末尾,最坏的时候需要移动整个顺序表,即插入位置是第一个元素,所以平均时间复杂度为
O(n)。插入操作移动节点的平均次数为:
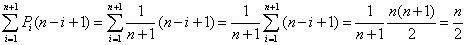
- 进行插入操作时,出于程序健壮性的要求,应当有
判断下标是否合法的语句。
2)删
- 根据指定值删除元素或根据指定下标删除元素,简称为按值删除和按址删除。
- 按址删除平均时间复杂度为
O(n),因为需要将指定下标后的元素都迁移一位,也就是说顺序表的删除就是用后一个存储单元中的内容覆盖当前存储单元的内容,所以移动元素之后一定记得更新顺序表的长度值,即更新为原来长度值减一。
- 按值删除的时间复杂度是
2O(n),因为进行删除之前还需要遍历顺序表元素以进行比较操作,从而找出指定值的元素的位置,然后再将该位置之后的元素都迁移一位。
- 从线性表中删除一个元素,所需的结点的平均移动次数为:
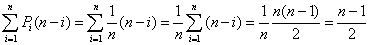
- 同样的要对操作的合法性进行检查,当下标大于顺序表表长时,会发生下标溢出,需要及时终止操作并返回错误信息给用户;但所要删除的值并不在顺序表中时,返回提示信息。
以下的改和查步骤都需要这一步。
3)改
- 此操作就是
给出指定元素的下标,然后更改该元素的值。由于顺序表的特性,可以直接根据下标确定元素的物理位置,因此此操作的时间复杂度都是常数阶。
4)查
- 指的是
根据元素值找出下标。其具体实现就是元素遍历和元素值比较,也即是说要获得指定值的下标,需要从顺序表表头元素开始到表尾元素结束,将每个元素都与指定值比较,若是第一次遇到相等的,就返回该下标。
- 因此最好的情况,指定值与表头元素相等,仅需比较一次,时间复杂度为
O(1)。
- 最坏的情况就是,指定值与表尾元素或不存在于顺序表中,需要比较 n 次,时间复杂度为
O(n)。
- 平均时间复杂度为
O(n)。
5)取值与遍历输出
- 取值就是根据所给下标,在下标合法的情况下,返回该下标对应元素的值。
- 遍历输出就是,从表头开始到表尾结束,将每个元素的值在屏幕中打印输出。
2.3、顺序表的排序
- 顺序表的排序可以分解为顺序表遍历、顺序表元素查找、顺序表元素修改三个基本操作。
- 排序的算法有很多,在后面专门介绍。我这里用的是最简单的
冒泡排序,该算法的原理就是”打擂台“,将当前元素与之后的每一元素进行大小比较,在降序排序的情况下,若其后的元素大于自身则与其互换值。
3、顺序表的优劣
- 顺序表在元素取值、元素修改操作上有很高效,这是顺序表的突出特点,而在元素插入和删除方面则表现不好。因此顺序表适用于频繁进行读取操作而很少进行修改操作的场景。
- 此外,顺序表的内存空间必须是连续的,当计算机内存紧张时,顺序表有可能就无法创建,因为内存中没有一片连续的足够大的空间可供申请。
三、顺序表的相关算法
1、取出最小元素
- 删除顺序表中值最小的元素并返回该值,空出的位置由最后一个元素填补;若顺序表为空则显示出错信息并退出运行。
bool DelMin(SeqList& L, int& value)
{
if (L.length == 0)
{
cout << "顺序表为空!" << endl;
return false;
}
value = L.data[0];
int pos = 0;
for (int i = 1; i < L.length; i++)
{
if (L.data[i] < value)
{
value = L.data[i];
pos = i;
}
}
L.data[pos] = L.data[L.length - 1];
L.length--;
return true;
}
2、顺序表翻转
void reverse(SeqList& L)
{
int temp;
for (int i = 0; i < L.length / 2; i++)
{
temp = L.data[i];
L.data[i] = L.data[L.length - i - 1];
L.data[L.length - i - 1] = temp;
}
}
3、全部删除指定值的元素
void delAllX(SeqList& l, int x)
{
int k = 0;
for (int i = 0; i < l.length; i++)
{
if (l.data[i] != x)
{
l.data[k] = l.data[i];
k++;
}
}
l.length = k;
}
4、范围删除
- 从有序顺序表中删除值位于[s,t]之间的所有元素,若s和t不合理或顺序表为空,则终止操作。
bool DelInS2T(SeqList& l, int s, int t)
{
int i, k = 0;
if (l.length == 0 || s >= t)
return false;
for (i = 0; i < l.length; i++)
{
if (l.data[i] >= s && l.data[i] <= t)
k++;
else
l.data[i - k] = l.data[i];
}
l.length -= k;
return true;
}
5、去重
- 从顺序表中删除重复值,使剩下的元素的值在顺序表中都是唯一的。
bool DeleteSame(SeqList& l)
{
if (l.length == 0)
return false;
int i;
int j;
for (i = 0, j = 1; j < l.length; j++)
{
if (l.data[i] != l.data[j])
{
l.data[++i] = l.data[j];
}
}
l.length = i + 1;
return true;
}
6、表合并
bool merge(SeqList A, SeqList B, SeqList& C)
{
if (A.length + B.length > C.length)
return false;
int i = 0, j = 0, k = 0;
while (i < A.length && j < B.length)
{
if (A.data[i] <= B.data[j])
C.data[k++] = A.data[i++];
else
C.data[k++] = B.data[j++];
}
while (i < A.length)
C.data[k++] = A.data[i++];
while (j < B.length)
C.data[k++] = B.data[j++];
return true;
}
7、交换或插入
- 在递增有序顺序表中查找指定值,若找到则与其后的元素交换位置,若找不到则插入。
- 递增顺序
void SearchExchangeInsertASC(SeqList& l, int x)
{
int low = 0;
int high = l.length - 1;
int mid;
while (low <= high)
{
mid = (low + high) / 2;
if (l.data[mid] == x)break;
else if (l.data[mid] < x)low = mid + 1;
else if (l.data[mid] > x) high = mid - 1;
}
if (l.data[mid] == x && mid != l.length - 1)
{
int t = l.data[mid];
l.data[mid] = l.data[mid + 1];
l.data[mid + 1] = t;
}
if (low > high)
{
int i = l.length - 1;
for (; i > high; i--)l.data[i + 1] = l.data[i];
l.data[i + 1] = x;
l.length += 1;
}
}
void SearchExchangeInsertDSC(SeqList& l, int x)
{
int low = 0;
int high = l.length - 1;
int mid;
while (low <= high)
{
mid = (low + high) / 2;
if (l.data[mid] == x)break;
else if (l.data[mid] < x)high = mid - 1;
else if (l.data[mid] > x) low = mid + 1;
}
if (l.data[mid] == x && mid != l.length - 1)
{
int t = l.data[mid];
l.data[mid] = l.data[mid + 1];
l.data[mid + 1] = t;
}
if (low > high)
{
int i = l.length - 1;
for (; i > high; i--)l.data[i + 1] = l.data[i];
l.data[i + 1] = x;
l.length += 1;
}
}
8、半域翻转
- 即将序列的前半部分与后半部分翻转,也即ab变成ba,调用时直接使用converse
void reverse(int R[], int from, int to)
{
int i, t;
for (i = 0; i < (to - from + 1) / 2; i++)
{
t = R[from + i];
R[from + i] = R[to - i];
R[to - i] = t;
}
}
void converse(int R[], int n, int p)
{
reverse(R, 0, p - 1);
reverse(R, p, n - 1);
reverse(R, 0, n - 1);
}
9、求A+B的中位数
int MSearch(int A[], int B[], int n)
{
int s1 = 0, d1 = n - 1, m1, s2 = 0, d2 = n - 1, m2;
while (s1 != d1 || s2 != d2)
{
m1 = (s1 + d1) / 2;
m2 = (s2 + d2) / 2;
if (A[m1] == B[m2]) return A[m1];
if (A[m1] < B[m2])
{
if ((s1 + d1) % 2 == 0)
{
s1 = m1;
d2 = m2;
}
else
{
s1 = m1 + 1;
d2 = m2;
}
}
if (A[m1] > B[m1])
{
if ((s2 + d2) % 2 == 0)
{
d1 = m1;
s2 = m2;
}
else
{
d1 = m1;
s2 = m2 + 1;
}
}
}
return A[s1] < B[s2] ? A[s1] : B[s2];
}
10、求主元素
- 所谓主元素就是一个在序列中重复出现的值并且重复出现的次数大于序列长度的一半。
- (0,5,5,3,5,7,5,5)的主元素是5,而(0,5,5,3,5,1,5,7)没有主元素。
- 当序列中存在主元素时返回主元素,否则返回-1。
int Majority(int A[], int n)
{
int t;
int i;
int count = 1;
t = A[0];
for (i = 1; i < n; i++)
{
if (A[i] == t)
count++;
else
{
if (count > 0)
count--;
else
{
t = A[i];
count = 1;
}
}
}
if (count > 0)
{
for (i = count = 0; i < n; i++)
{
if (A[i] == t)
count++;
}
}
if (count > n / 2) return t;
else return -1;
}
11、求最小正整数
- 给定一个 n 长的序列,从中找出1~n中没有在序列中出现的最小正整数。
- 例如,(-5,3,2,3)的最小正整数就是1,(1,2,3)的最小正整数是4。
int findMissMin(int a[], int n)
{
int i;
int* b = new int[n];
memset(b, 0, sizeof(int) * n);
for (i = 0; i < n; i++)
if (a[i] > 0 && a[i] <= n)
b[a[i] - 1] = 1;
for (i = 0; i < n; i++)
if (b[i] == 0)break;
return i + 1;
}