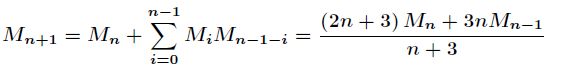卡特兰数 默慈金数 默慈金三角形 反射原理
卡特兰数
公式
递推式： f ( n ) = ∑ f ( i ) ∗ f ( n − i − 1 ) f(n) = ∑f(i) * f(n-i-1) f(n)=∑f(i)∗f(n−i−1) 0 ≤ i ≤ n − 1 0≤i≤n-1 0≤i≤n−1
变式1： f ( n ) = C ( n 2 n ) / ( n + 1 ) f(n) = C\tbinom{n}{2n} / (n+1) f(n)=C(2nn)/(n+1)
变式2： f ( n ) = C ( n 2 n ) f(n) = C\tbinom{n}{2n} f(n)=C(2nn) - C ( n + 1 2 n ) C\tbinom{n+1}{2n} C(2nn+1) （应用最广）
变式3： f ( n ) = f ( n − 1 ) ∗ ( 4 ∗ n − 2 ) / ( n + 1 ) f(n)=f(n-1)*(4*n-2)/(n+1) f(n)=f(n−1)∗(4∗n−2)/(n+1)
应用：
问题1 ：
n个-1和n个+1排成2n个数。要求任意前k个数和大于等于0。求放置方案数（《组合数学》 P168）
解法：
全集为 C ( n 2 n ) C\tbinom{n}{2n} C(2nn)
对于不合理集和，假设取最小的k使得a1+…+ak = -1。且易得ak=-1,a1+…+ak-1 = 0。
将前k个数1变成-1，-1变成1。得到一个新的数列b1,b2,b3…b2n。
可知b数列1的个数为n+1, -1的数目为n-1。每一个这样的b数列，都能对应一个相应的不合理a数列。
而b数列个数为 C ( n + 1 2 n ) C\tbinom{n+1}{2n} C(2nn+1)
所以合理a数列数目为 C ( n 2 n ) C\tbinom{n}{2n} C(2nn) - C ( n + 1 2 n ) C\tbinom{n+1}{2n} C(2nn+1)（变式2）
这被称为反射原理。在《计算机程序设计艺术第一卷》P508有相应介绍
类似的，只要满足类似的限制关系：n个x n个y放置，且满足任意前k个数里面x ≥ y（这个关系可以被定量化），就是卡特兰数。
变式1：
- n个左括号，n个右括号匹配方式数：左括号大于等于右括号。
- n个数，进出栈方式：进栈数小于等于出栈数。
- n个0，n个1，且任意前k个数0的数目不小于1的数目：0,1数目限制关系。
- 2n个数排成2行，每行递增，且第二行对应数大于第一行。可变形为n个0,n个1放置。0表示对应的人在第一排，1表示对应的人在第二排。那么只要0数目大于等于1，那么就合理（左数和上数确定，当前数肯定确定了）。转化为问题2。
- 售票问题：n个50元和n个100元，要求能够找零。限制关系明显。
上述讨论的问题都是代数式的。对应也有几何式的问题。
问题2:
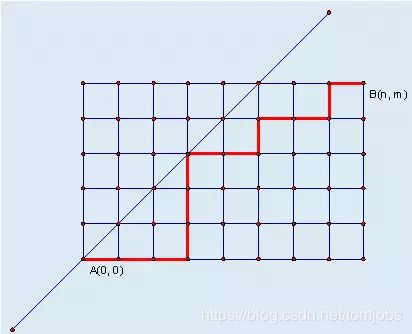
n ∗ n n*n n∗n 的格子，可以向左走也可以向上走，不可以穿过y = x的线。求从(0,0)走到(n,n)有多少种方式。
解法：
限制关系其实很明显：向x走的步数不大于向y走的步数。由此转化为了问题1。
变式1：
BZOJ3907
那么假设终点是(n,m)怎么办呢？
首先我们知道总方案数是： C ( n n + m ) C\tbinom{n}{n+m} C(n+mn)
只要算出不合理方案就可以得到合理方案数，怎么算呢？
其实在问题1的时候我们就已经算出来了。
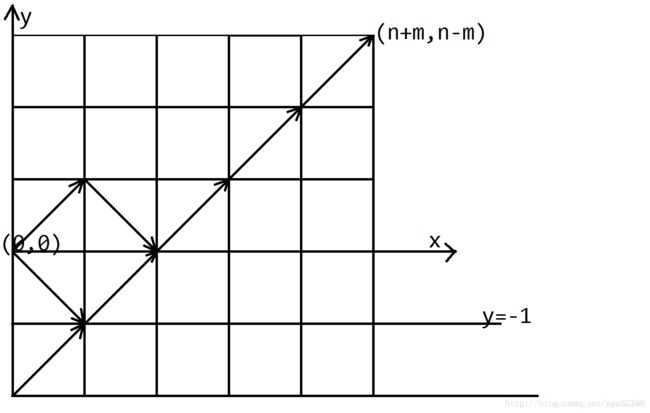
问题1中我们对数列用了反射原理，同理在此处运用反射原理，在第一次穿过y = x线的地方进行对称，对称点为(-1,1)，关于y = x + 1对称（画图可以看出来）
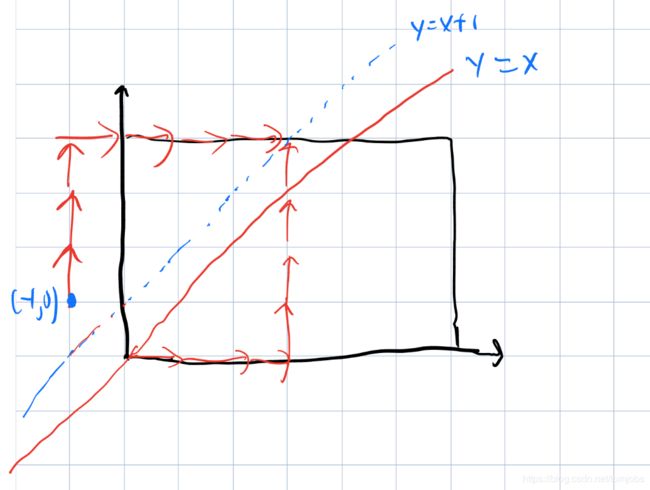
假设第一次发生不合理是第k步。那么将前k步反过来。可以得到n+1步走向x，m-1步走向y。
得到不合理方案为： C ( n + 1 n + m ) C\tbinom{n+1}{n+m} C(n+mn+1)
答案为 C ( n n + m ) C\tbinom{n}{n+m} C(n+mn) - C ( n + 1 n + m ) C\tbinom{n+1}{n+m} C(n+mn+1)
变式2：
P1641 [SCOI2010]生成字符串
假设n个1，m个0。要求任意前k个数1的个数不小于0的个数。
反射原理可以秒解。几何表示也同变式1
（图自洛谷 xyz32768）
题解会写按照y = -1对称反转前k步。其实就是反射原理的几何表示。当然用几何表示更为直观。
默慈金三角形
公式
写题时候发现的东西，资料不是很多，参考一下吧。
当 n = 1 时。
f(1,0) = f(1,1) = 1.
当 n ≥ 2 , m = 0 n ≥ 2,m = 0 n≥2,m=0
f ( i , j ) = f ( i − 1 , j ) + f ( i − 1 , j + 1 ) f(i,j) = f(i-1,j) + f(i-1,j+1) f(i,j)=f(i−1,j)+f(i−1,j+1)
当 n ≥ 2 , m ≥ 1 n ≥ 2,m ≥ 1 n≥2,m≥1
f ( i , j ) = f ( i − 1 , j − 1 ) + f ( i − 1 , j ) + f ( i − 1 , j + 1 ) f(i,j) = f(i-1,j-1) + f(i-1,j) + f(i-1,j+1) f(i,j)=f(i−1,j−1)+f(i−1,j)+f(i−1,j+1)
1: 1 1
2: 2 2 1
3: 4 5 3 1
4: 9 12 9 4 1
5: 21 30 25 14 5 1
6: 51 76 69 44 20 6 1
7: 127 196 189 133 70 27 7 1
8: 323 512 518 392 230 104 35 8 1
9: 835 1353 1422 1140 726 369 147 44 9 1
10: 2188 3610 3915 3288 2235 1242 560 200 54 10 1
应用
问题1
CF896D
假设售货亭有票没前，50元一张票，n个人，有50元和100元，或者可以选择刷卡。求售货亭剩下k个50元的方案数。
答案对应于 默慈金三角形 的 f ( n , k ) f(n,k) f(n,k).
其实这也可以看做卡特兰数的一个变形，相当于是问题2，只不过多了一个不放数字的过程。那么就要多枚举一次，可以推出一个n方公式。
（博主不才，只推出了n方，但肯定是可以优化的）
对于所有的 i - j = k 相加就是答案。
C ( i n ) C\tbinom{i}{n} C(ni) ( C ( ( i − k ) / 2 i ) C\tbinom{(i-k)/2}{i} C(i(i−k)/2) - C ( ( i − k ) / 2 − 1 i ) C\tbinom{(i-k)/2-1}{i} C(i(i−k)/2−1))
如果问题变成求 l ≤ k ≤ r l ≤ k ≤r l≤k≤r的和
那么全部加起来以后，中间消掉了，变成
C ( i n ) C\tbinom{i}{n} C(ni) ( C ( ( i − l ) / 2 i ) C\tbinom{(i-l)/2}{i} C(i(i−l)/2) - C ( ( i − r ) / 2 − 1 i ) C\tbinom{(i-r)/2-1}{i} C(i(i−r)/2−1))
默慈金数
公式
（图自Acdreamer)
也可以看作卡特兰数的变形。
意义
对于其公式证明资料不多（英文）。
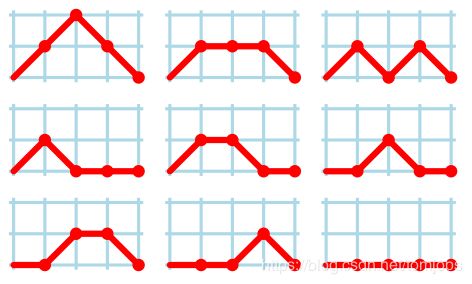
其意义为：n个格子，可以放1，可以放0，也可以不放，要求前k个数1的个数不小于0的个数，要求最后1的个数等于0的个数。求方案数。
同时对应的是默慈金三角形的第一列。相当于售票处剩下0个50元。
假设有2i个格子放了数字，单独考虑这2i个格子实际就是卡特兰数。那么就是在n个格子里面选2i个格子，再乘上卡特兰数。（公式2）
公式2也可以看作默慈金三角形公式的一个特例。
应用
问题1
hdu5673 Robot
从(0,0)出发，可以向左走，可以向右走，可以不走，走n次，不可以走入负轴。求最后走回原点的方案数。
裸的默慈金数
问题2
51nod 1556 计算.
有一个1*n的矩阵 固定第一个数为1 其他填正整数 且相邻数的差不能超过1 求方案数%1e9+7的结果
实际是问题1变形为，终点为大于等于0的任何位置。
假设M数列为回到原点的方案（默慈金数），F数列为任意合理位置的方案数。
对应 M(1) = 1,M(2) = 2
F(0) = 1,F(1) = 2, F(2) = 5.
F(n) = F(n - 1) * 3 - M(n - 1)。
答案为 F(n-1)。
实际F数组对应的是默慈金三角形的行和。