数据结构期末复习小结

最小生成树

Kruskal(克鲁斯卡尔)算法

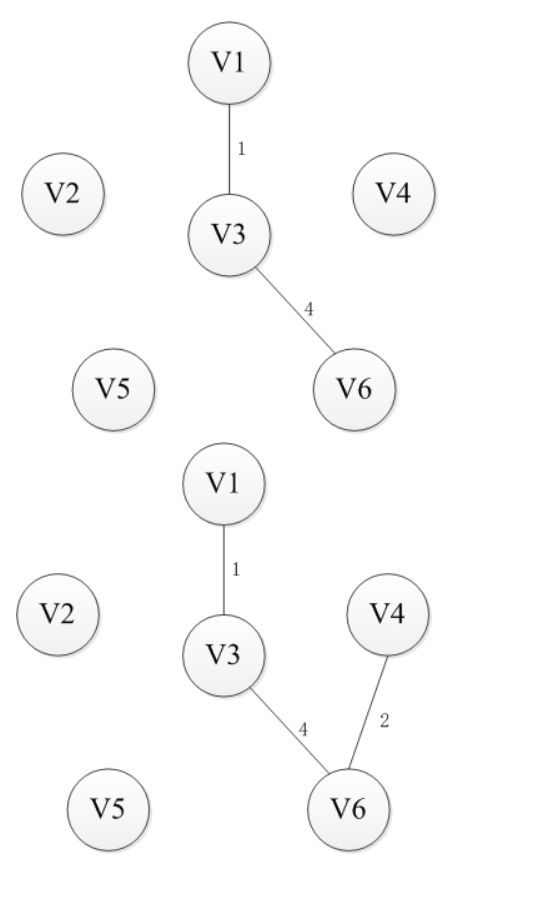
最小生成树，算法思想：首先按照边的权值进行从小到大开始排序，每次从剩余的边中选择权值较小的且边的两个顶点不在同一个集合内的边，加入到生成树，直到n-1条边为止。（并查集，并且在查找集合中涉及路径压缩）图解如下

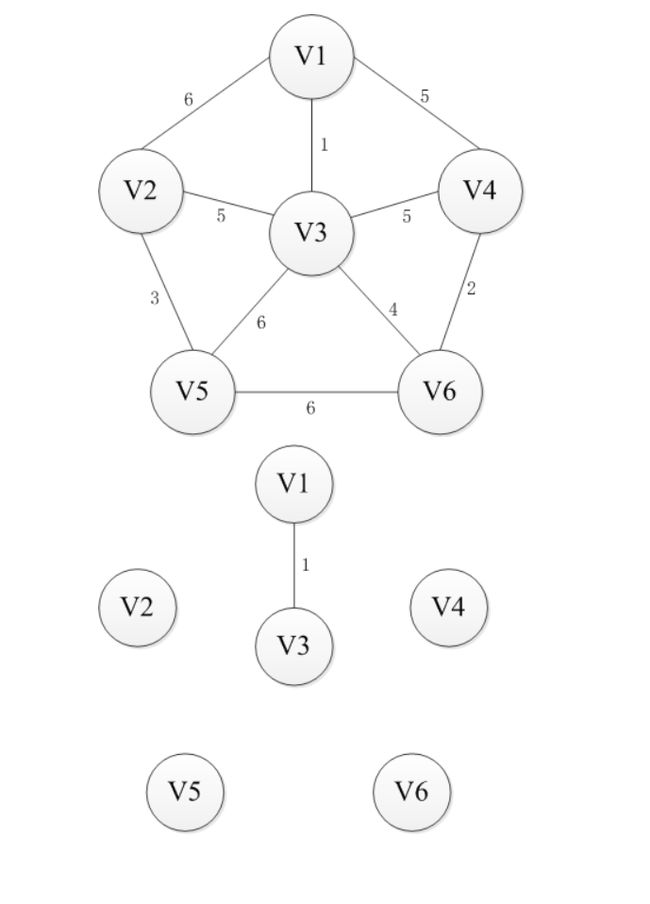
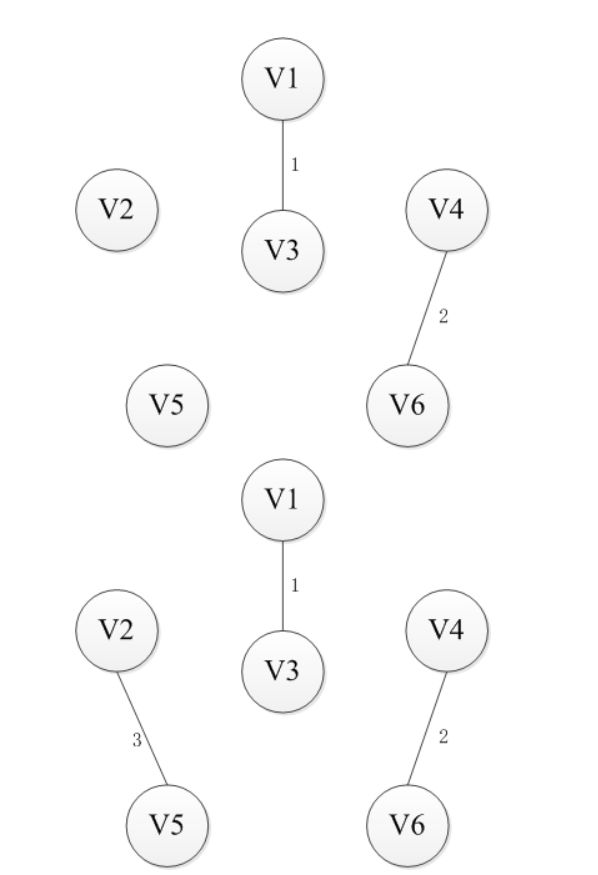
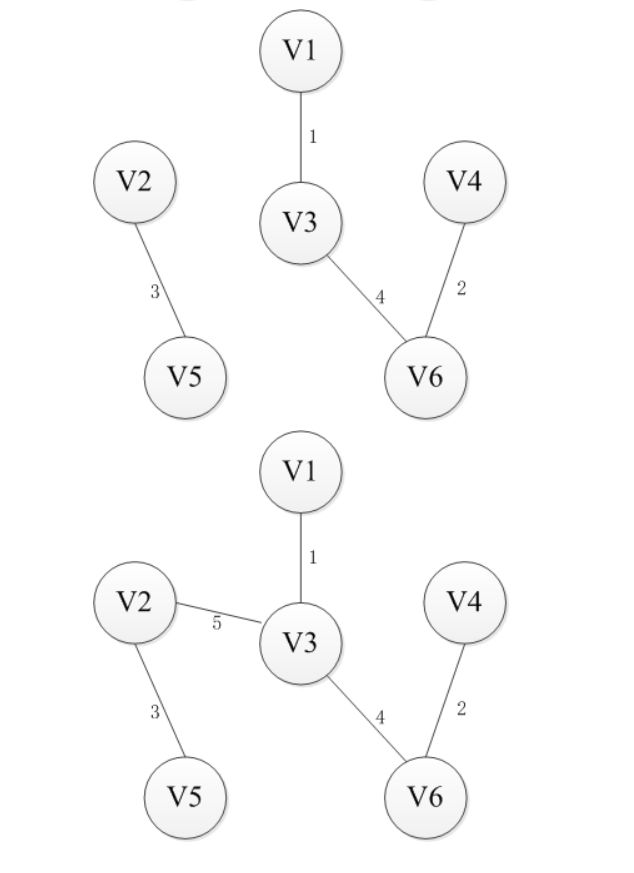
prime（普利姆）算法

将顶点分为两类，树顶点（已被选入生成树的顶点），非树顶点（还未被选入生成树的顶点），首先选择任意一个顶点加入生成树，接下来要找出一条边添加到生成树，这需要枚举每一个树顶点到每一个非树顶点的所有边，然后找到最短边加入到生成树，照此方法，重复操作n-1次，直到将所有顶点加入到生成树中

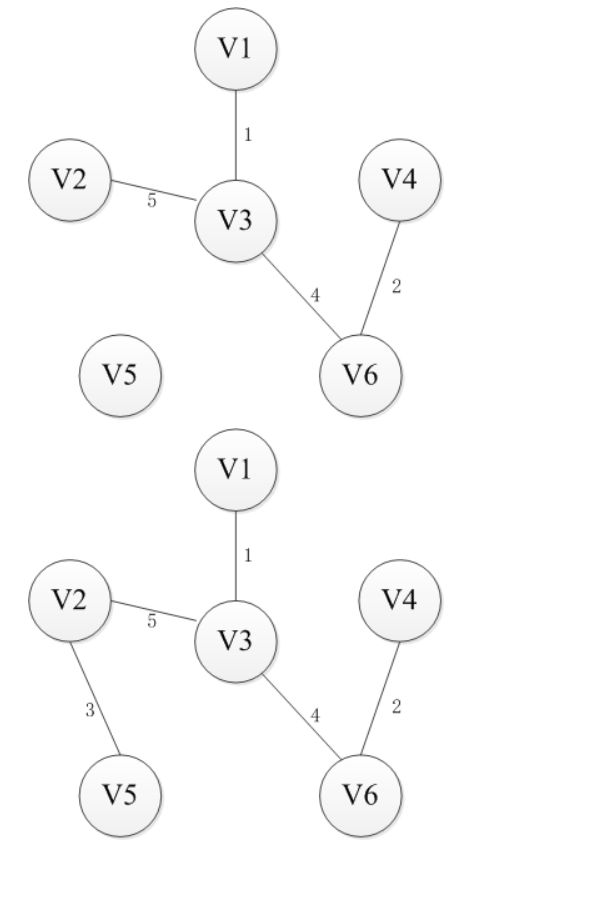
最短路

Floyd（弗洛伊德）算法

解决的是多源最短路径的问题，就是任意两点通过中转点找到最短路径

Dijkstra(迪杰斯特拉)算法

单源最短路

哈夫曼编码

致读者： 博主是一名数据科学与大数据专业大二的学生，真正的一个互联网萌新，写博客一方面是为了记录自己的学习历程，一方面是希望能够帮助到很多和自己一样处于困惑的读者。由于水平有限，博客中难免会有一些错误，有纰漏之处恳请各位大佬不吝赐教！之后会写大数据专业的文章哦。尽管当前水平可能不及各位大佬，但我会尽我自己所能，做到最好☺。——天地有正气，杂然赋流形。下则为河岳，上则为日星。

假设用于通信的电文由字符集{a,b,c,d,e,f,g}中的字母构成。它们在电文中出现的频度分别为{0.31,0.16,0.10,0.08,0.11,0.20,0.04}

为这7个字母设计哈夫曼编码

为这7个字母设计等长编码，至少需要几位二进制数？

哈夫曼编码比等长编码使电文总长压缩多少？

请画出哈夫曼树的构造过程

对于这个题目来说，要简单也真的简单，最重要的是我们要理解哈夫曼编码的本质。

确定权值

在这里我们先统计各个字符出现的权值，当然用0.31 是可以的，但是由于写博客的原因，我就暂时，假定有100个字符，也就是写成整数权值 31。

于是我们得到一个权重表（从小到大排序）

字符	权值
g	4
d	8
c	10
e	11
b	16
f	20
a	31

然后我们把权值对应的信息存储到一个 结点 中，并假定这些结点都存储到队列里面，这个队列都按照权值从小到大的顺序排序。

初始化结果：

建树

每次从队列中取出两个结点。然后构成一个结点，重新放回队列。

然后再次重复操作，直至，队列剩余一个结点为止。

编码

上面的树我已经编号码了。唔…失误失误

按照编码的规则，从根节点开始往左边的结点 编码 0 往右边的结点编码 1。

直到到达叶子结点，然后叶子结点对应的编码就是从根节点到叶子结点编码连起来。

等长编码

对于一个无记忆离散信源中每一个符号，若采用相同长度的不同码字代表相应的符号，就称为等长编码。一般来说，若要实现无失真的编码，这不但要求信源符号与码字是一一对应的，而且要求码符号序列的反变换也是唯一的。也就是说，一个码的任意一串有限长的码符号序列（码字）只能被唯一地翻译成所对应的信源符号序列。

说那么多干啥，一点用都没有。

所谓的等长编码：例如对字符串 “ac“ 来说，只要两个字符，所以我们可以使用 0 或者 1 来编码。

最常见的就是 ASSIC 编码，8位等长的二进制0-127来表示字符。

同样的道理，这个题目中一共有 7 不同个字符，所以我们应该如何表示呀，肯定就是找到最小的2^n大于7，显然这个就是3，类似的思想还有老鼠试毒药的问题。

关于压缩的计算，就更简单了。如图：

拓展与思考

为什么哈夫曼编码能够压缩或者加密呢？

个人认为是因为对于这样的存储方法，其实是有频数最多的字符，往靠近根结点的地方建树，而频数较低的，就往深处或者底部，建立结点。这样的话，对于 频数 较高的字符获得的编码长度比较小，而 频数 小的字符获得的编码长度长。

举个例子：

对于98个字符‘a’和1个字符’b‘和1个字符’c‘

如果用等长的二进制编码，至少需要两位，但是98个’a‘占用的空间就显得浪费了。

后记：博主终于码完了，如果觉得以上内容有帮助的话，能不能留下你的小心心呢？❤你的赞和支持，就是博主最大的动力！！

邻接表和邻接矩阵

问题：
( 15分 )

某国有7个城市，它们互相之间没有公路相通，因此交通十分不便。为解决这一“行路难”的问题，政府决定修建公路，经过调研，如果把这7个城市之间的关系看成一个图，字母代表城市名称，数字代表修路的花费：

请回答以下问题：

（1）请画出该图对应的邻接表，并写出深度优先和广度优先遍历序列

（2）为了最大限度的节约资金，政府只允许修6条路，通过这6条路就能把这7个城市相连通，请从城市A出发用普利姆算法进行6条路的选择，画出求解过程。

提示：一个图的邻接表答案不唯一，但是邻接表对应的遍历序列答案是唯一的。

该图是带权图，邻接表中也要存储每条边的权值信息。

答案及解析（如有不对，欢迎指正）
(1)

邻接表如下

深度优先序列为：ABCDFEG

广度优先序列为：ABDGCFE

标准答案：

DFS序列：A B C D F E G

BFS序列：A B D G C F E

(2)

标准答案：

平衡二叉排序树

问题

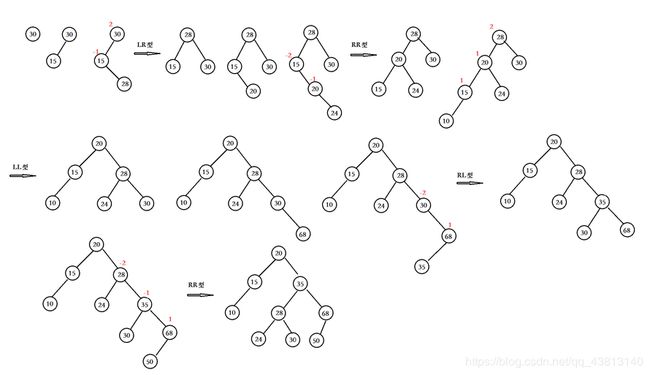
依次输入表（30,15,28,20,24,10,68,35,50）中的元素，生成一棵平衡的二叉排序树。请画出构造过程，并在其中注明每一次平衡化的类型（LL型、RR型、LR型、RL型）

标准答案：

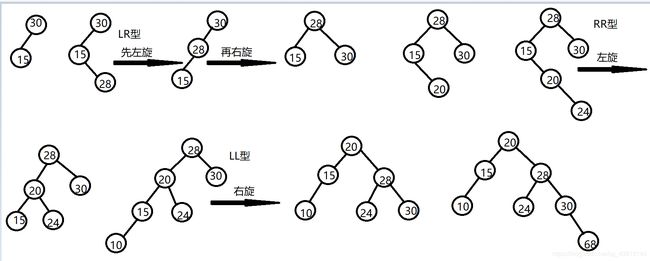
平衡树思想

在网上找到比较好理解的图解

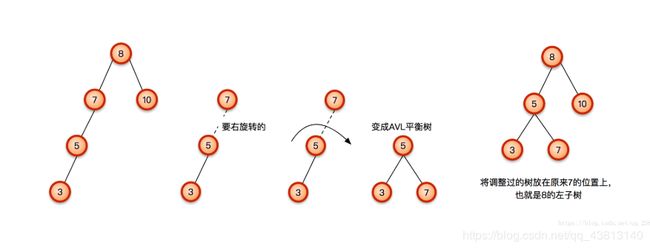
LL型右旋转
因为左子树5的高度更高，所以要把左子树5向上提一下，这时旋转就很明显了，抓着5向上一提，7就掉到5的右边了，成了5的右子树。

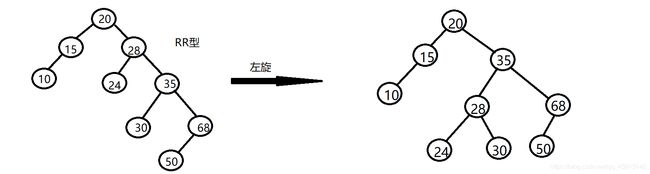
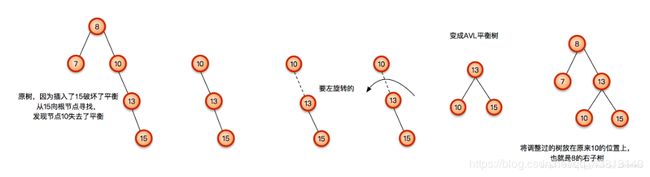
RR型左旋转

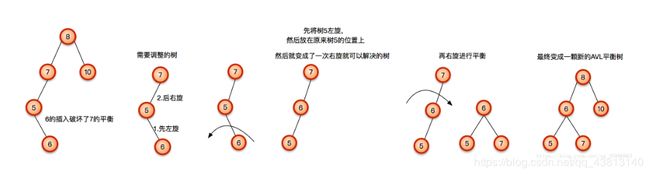
LR型 先左旋再右旋

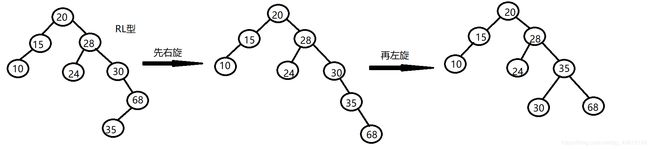
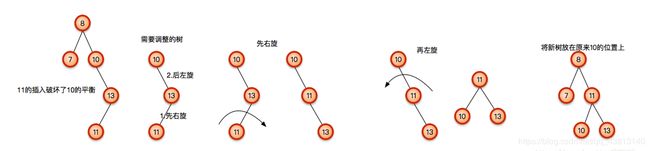
RL 先右旋再左旋

总结：
LL 右旋转
RR 左旋转
LR 先左旋后右旋
RL 先右旋后左旋

哈希

给定一组查找关键字(19,14,23,1,65,20,84,27,55,11,10,79)

哈希函数为：H(key)=key % 13, 哈希表长为m=15，设每个记录的查找概率相等。

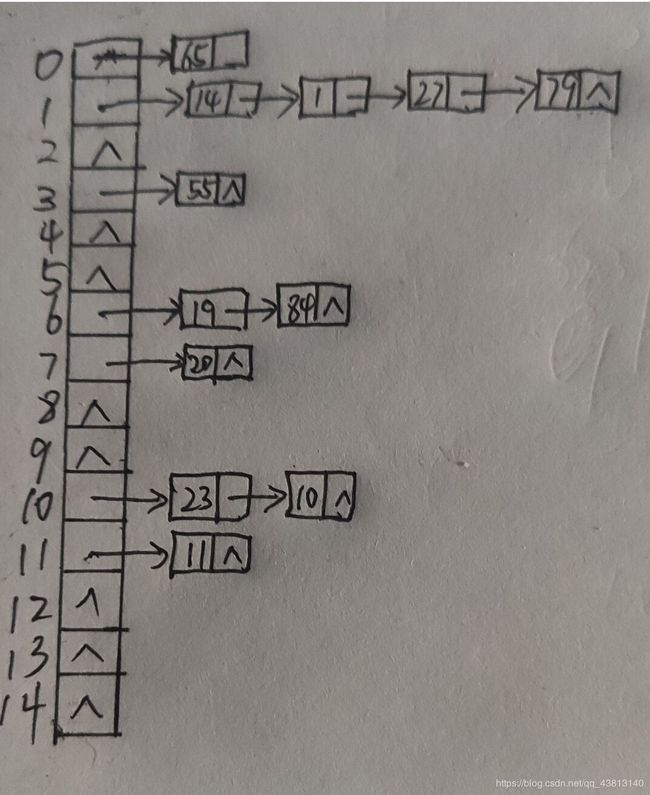
1. 请画出按照线性探测再散列处理冲突得到的哈希表（给出求解过程），并计算查找成功和查找失败时的平均查找长度各是多少。

2. 请画出按照链地址法处理冲突得到的哈希表，并计算查找成功和查找失败时的平均查找长度各是多少。

ps:老师改题啦，原来和下面的那题是一样的，题目任你改做不出算我输，哈哈哈（低调低调）

由第一个H（19） = 19MOD 13 = 6以此类推

19	14	23	1	68	20	84	27	55	11	10	79
6	1	10	1	0	7	6	1	3	11	10	1

可以得到散列表为

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
65	14	1	21	55	79	19	78	84		23	11	10

key	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
count	1	1	2	3	2	5	1	1	3		1	1	3

查找成功的平均长度：（1+1+2+3+2+5+1+1+3+1+1+3）÷12 = 24/12 = 2;

key	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
count	10	9	8	7	6	5	4	3	2	1	4	3	2

查找失败得平均长度：（10+9+8+7+6+5+4+3+2+1+4+3+2）÷13 = 64/13；

（2）

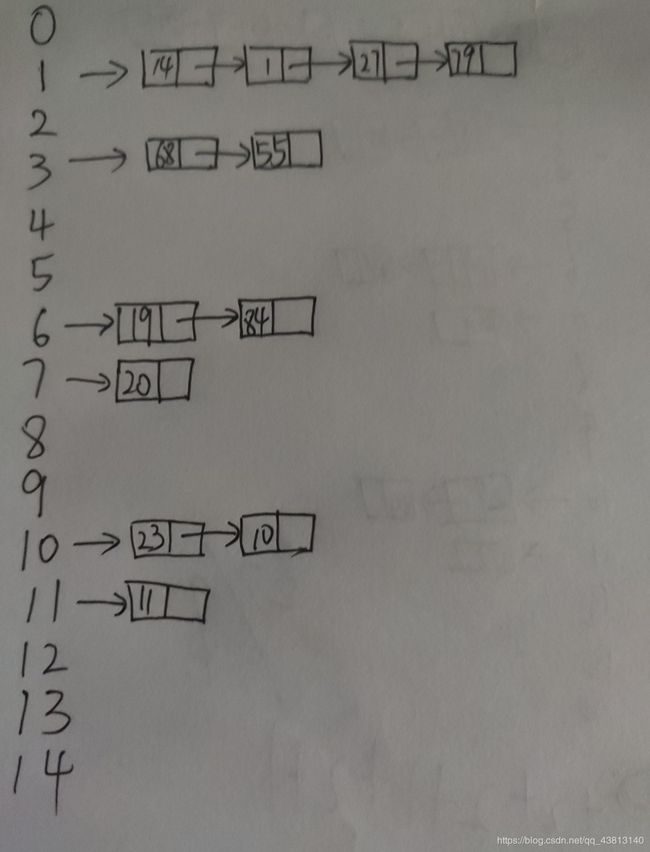
链地址法：

查找成功的平均长度：（1×7+2×3+3×1+4×1）÷12 = 20/12=5/3；

查找失败的平均长度：（2+5+1+2+1+1+3+2+1+1+3+2+1）÷13 = 25/13；

**请回答采用线性探测再散列和链地址法处理冲突构建的哈希表中，查找失败时的平均查找长度如何计算？

例：已知一组关键字(19,14,23,1,68,20,84,27,55,11,10,79)

​ 哈希函数为：H(key)=key MOD 13, 哈希表长为m=15，

​ 设每个记录的查找概率相等，采用以上两种方法处理冲突，查找失败时的平均查找长度各是多少**

这题可真得是出到点子上去啦，看视频，找资料，网上有得解释真的是有点误人子弟，随后加上问了老师一番才有了确定的结果

没错我们主要得难点还是查找失败得分母到底是什么呢，还有一个网上解释错得，但广为流传得，

但是还是全部体系得去写吧毕竟也许以后就忘了

线性探测

（1）

有第一个H（19） = 19MOD 13 = 6，后面得以此类推，

19	14	23	1	68	20	84	27	55	11	10	79
6	1	10	1	3	7	6	1	3	11	10	1

可以得到散列表为

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
	14	1	68	27	55	19	20	84	79	23	11	10

key	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
count		1	2	1	4	3	1	1	3	9	1	1	3

查找成功的平均长度：（1+2+1+4+3+1+1+3+9+1+1+3）÷12 = 30/12 = 2.5;

key	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
count	1	13	12	11	10	9	8	7	6	5	4	3	2

查找失败得平均长度：（1+13+12+11+10+9+8+7+6+5+4+3+2）÷13 = 7

ps:查找失败得平均长度分母是MOD后面得数也就是13

（2）链地址法：

查找成功的平均长度：（1×6+2×4+3×1+4×1）÷12 = 21/12；

查找失败的平均长度：（1+5+1+3+1+1+3+2+1+1+3+2+1）÷13 = 25/13；

ps：它的分母也是mod后面的数13 ，并且查的范围是0-12；

线性探测法例题

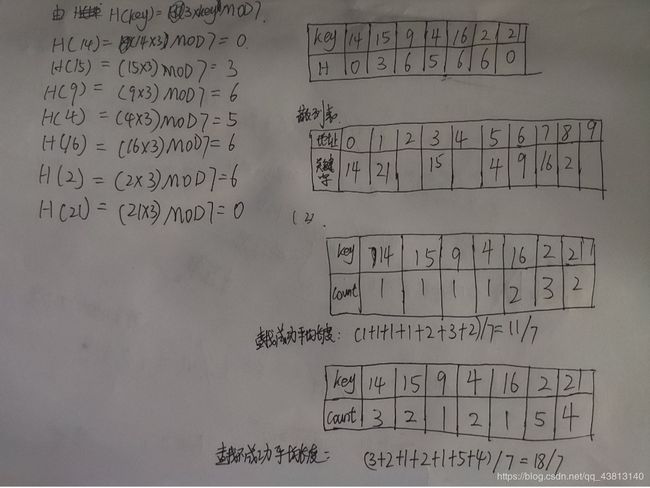
将关键字序列（14、15、9、4、16、2、21）散列存储到散列表中。散列表的存储空间是一个下标从0开始的一维数组。散列函数为： H(key) = (key x 3) MOD 7，处理冲突采用线性探测再散列法，要求装填因子为0.7。
(1) 请画出所构造的散列表；
(2) 分别计算等概率情况下查找成功和查找不成功的平均查找长度。

当时由于老师让及时做出来，就有点匆忙，能懂哪个意思就行

链地址法例题

题目
将关键字序列{1 13 12 34 38 33 27 22} 散列存储到散列表中。散列函数为：H(key)=key mod 11，处理冲突采用链地址法，求在等概率下查找成功和查找不成功的平均查找长度

1mod11=1，所以数据1是属于地址1
13mod11=2，所以数据13是属于地址2
12mod11=1，所以数据12也是属于地址1（这个数据是数据1指针的另一个新数据）
34mod11=1，所以数据34是属于地址1（这个数据是数据12指针的另一个新数据）
38mod11=5，所以数据38是属于地址5
33mod11=0，所以数据33是属于地址0
27mod11=5，所以数据27是属于地址5，（这个数据是数据38指针的另一个新数据）
22mod11=0，所以数据22是属于地址0，（这个数据是数据33指针的另一个新数据）

链地址法处理冲突构造所得的哈希表如下：

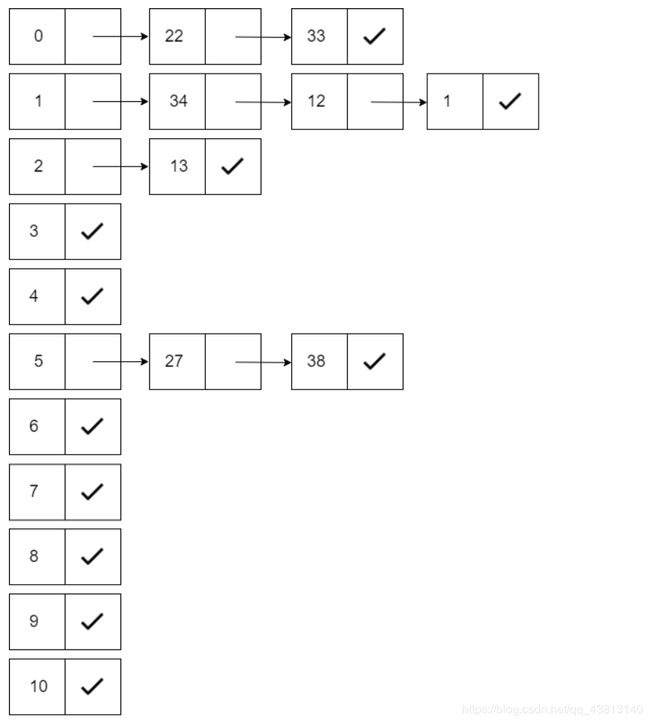
查找成功时： ASL=（3×1+2×3+1×4）/8=13/8，

查找不成功时：ASL=(3+4+2+1+1+3+1+1+1+1+1)/11=19/11；或者 ASL=(7×1+1×2+2×3+1×4 )/11=19/11，

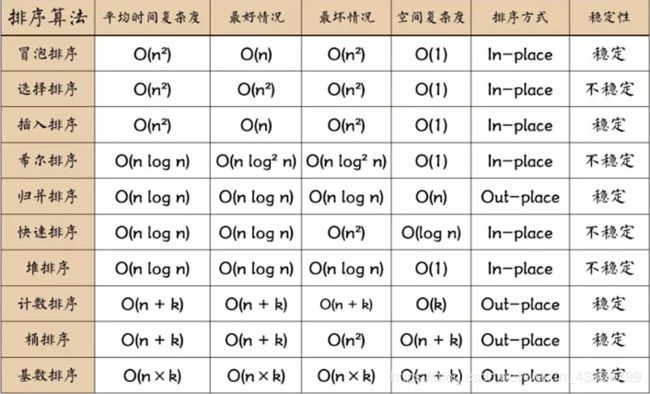
排序

树小结

1.节点的度：一个节点含有的子树的个数称为该节点的度；

2.树的度：一棵树中，最大的节点度称为树的度；

3.叶节点或终端节点：度为零的节点；

4.非终端节点或分支节点：度不为零的节点；

5.父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；

6.孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；

7.兄弟节点：具有相同父节点的节点互称为兄弟节点；

8.节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

9.深度：对于任意节点n,n的深度为从根到n的唯一路径长，根的深度为0；

10.高度：对于任意节点n,n的高度为从n到一片树叶的最长路径长，所有树叶的高度为0；

11.堂兄弟节点：父节点在同一层的节点互为堂兄弟；

12.节点的祖先：从根到该节点所经分支上的所有节点；

13.子孙：以某节点为根的子树中任一节点都称为该节点的子孙。

14.森林：由m（m>=0）棵互不相交的树的集合称为森林；

顺序表操作集

 
/* 你的代码将被嵌在这里 */
List MakeEmpty(){
    List L = (List)malloc(sizeof(struct LNode));
    L->Last = -1;
    return L;
}
Position Find( List L, ElementType X ){
    for(int i = 0; i <= L->Last; i++)
        if(X == L->Data[i])
            return i;
    return ERROR;
}
bool Insert( List L, ElementType X, Position P ){
    if(L->Last == MAXSIZE - 1){
        printf("FULL");
        return false;
    }
    //插入的位置是否合法
    if(P < 0 || P > L->Last + 1){
        printf("ILLEGAL POSITION");
        return false;
    }
    for(int i = L->Last + 1; i > P; i--)
        L->Data[i] = L->Data[i - 1];
    L->Data[P] = X;
    L->Last++;
    return true;
}
bool Delete( List L, Position P ){
    if(P < 0 || P > L->Last){
        printf("POSITION %d EMPTY",P);
        return false;
    }
    for(int i = P; i < L->Last; i++)
        L->Data[i] = L->Data[i + 1];
    L->Last--;
    return true;
}

带头结点的链式表操作集

/* 你的代码将被嵌在这里 */
List MakeEmpty(){
    //分配空间
    List head = (List)malloc(sizeof(struct  LNode));
    //设置数据和指向
    head->Data = 0;
    head->Next = NULL;
    return head;
}
bool Insert( List L, ElementType X, Position P ){
    List apply = NULL;
    while(L->Next != P && L->Next != NULL)
        L = L->Next;
    if(L->Next == NULL && P != NULL){
        //如果已经到了链尾,说明P肯定不在链表里，而此时P又不为NULL，则一定是P出现了错误 
        printf("Wrong Position for Insertion\n");
        return false;        
    }else{
        //有三种情况：第一种L->Next!=NULL，P！=NULL是普通情况 
        //第二种L->Next!=NULL，P==NULL 这种情况不存在，
        //因为若P==NULL，则退出while循环后L->Next或者走到L->Next=NULL或者L->Next=P仍为NULL，所以此种情况不存在。 
        //第三种L->Next==NULL，P==NULL 则插在链表末尾
        apply = (List)malloc(sizeof(struct LNode));
        apply->Data = X;
        L->Next = apply;
        apply->Next = P;
        return true;
    }
}
Position Find( List L, ElementType X ){
    while(L->Next != NULL){
        if(L->Next->Data == X){
            return L->Next;
        }
        L = L->Next;
    }
    return ERROR;
}
bool Delete( List L, Position P ){
    if(L->Next== NULL||P==NULL){    //如果只有头结点或者删除的位置是NULL，则不能删除 
        printf("Wrong Position for Deletion\n");
        return false;        
    }
    while(L->Next != P && L->Next != NULL)
        L = L ->Next;
    if(L->Next == NULL){    //P一定在链表上，如果始终没有找到P，则删除错误 
        printf("Wrong Position for Deletion\n");
        return false;        
    }
    else{   //否则删除P 
        L->Next = P->Next;
        free(P);
        return true;
    }
}

树的四种遍历

void InorderTraversal( BinTree BT ){
    //left root right
    if(!BT) return;
    InorderTraversal(BT->Left);
    printf(" %c", BT->Data);
    InorderTraversal(BT->Right);
}
void PreorderTraversal( BinTree BT ){
    //root left right
    if(!BT) return;
    printf(" %c", BT->Data);
    PreorderTraversal(BT->Left);
    PreorderTraversal(BT->Right);
}
void PostorderTraversal( BinTree BT ){
    //left right root
    if(!BT) return;
    PostorderTraversal(BT->Left);
    PostorderTraversal(BT->Right);
    printf(" %c", BT->Data);
}
void LevelorderTraversal( BinTree BT ){
    BinTree a[100];
    int Left = 0, Right = 0;
    a[Right++] = BT;
    if(!BT) return;
    while(Left != Right){
        printf(" %c", a[Left]->Data);
        if(a[Left]->Left) a[Right++] = a[Left]->Left;
        if(a[Left]->Right) a[Right++] = a[Left]->Right;
        Left++;
    }
}