动态规划 简单题目集锦（一） UPC

题目

探索数字迷塔

题目描述
晶晶最近迷上了数字迷宫游戏，整天沉浸在一串串看似简单的数字中自得其乐。数字迷宫游戏的魅力体现在变化中隐含着不变的规律，归纳是探究数字迷宫的法宝之一。下图就是一个由线连接起来的数字小方格组成的数字迷塔。

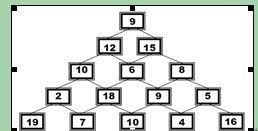
这个迷塔共n层，它由n×(n+1)/2个小方格组成。每个小方格中都有一个数字，并且连着下一层的两个小方格。现从塔顶走到塔底，每一步只能走到相邻的方格中，则经过方格的数字之和最大值是多少？这个问题晶晶已经琢磨一天了，她感觉异常棘手。你能帮帮她吗？

输入
输入数据共n+1行，第1行是一个整数n(1≤n≤1000)，表示数字迷塔的高度，接下来用n行数字表示数字迷塔，其中第i行有i个正整数，且所有的正整数均不大于100。

输出
输出可能得到的最大和。

样例输入
5
9
12 15
10 6 8
2 18 9 5
19 7 10 4 16
样例输出
59

提示
样例说明：9→12→10→18→10

AC代码：

#include 

using namespace std;
int a[1010][1010];
int dp[1010];

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= i; j++) {
            scanf("%d", &a[i][j]);
            dp[j] = a[i][j]; //初始化第n层
        }
    }
    for (int i = n - 1; i >= 1; i--) {//从第n-1层往上
        for (int j = 1; j <= i; j++) {//dp[j]表示从第i层一直到第n层最大的数字之和  第i层的每一个都选它左下方和右下方的最大的，
            dp[j] = max(dp[j] + a[i][j], dp[j + 1] + a[i][j]);//空间优化 用一维数组，每次更新后，之前的都用不到了
        }
    }
    printf("%d\n", dp[1]);
    return 0;
}

圣诞树

题目描述
圣诞特别礼物挂在一棵圣诞树上，这棵树有n层，每层有一件礼物，每件礼物都有一个价值，有的礼物还有一些连接线，与下层的礼物相连。领取礼物的规则如下：任选一件礼物，它的下面如果有连接线，则可以继续取它连接的礼物，依此类推直至取到没有连接线的礼物才结束。你如果是第一个去取，怎样取才能获得最大的价值呢？请你编一程序解决这一问题。

输入
第1行只有一个数据n(n≤100)，表示有n层礼物，以下有n行数据，分别表示第1～n层礼物的状态，每行至少由一个数据构成，且第一个数据表示该礼物的价值，后面的数据表示它与哪些层的礼物相连，如果每行只有一个数据则说明这层礼物没有与下层礼物相连，每个数据大小均不超过10000。

输出
只有一个数，表示获得的最大价值。

样例输入
3
12 2 3
20
30
样例输出
42

AC代码

#include 

using namespace std;
struct node {
    int val;
    int l[102];
    int c;
} a[110];
int dp[110];//dp[i]表示从i开始到最后所能获得的最大价值

int main() {
#ifdef ONLINE_JUDGE
#else
    freopen("in.txt", "r", stdin);
#endif

    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i].val);
        int cnt = 0;
        while (getchar() == ' ') {
            scanf("%d", &a[i].l[++cnt]);
        }
        a[i].c = cnt;
    }
    int ans = 0;
    //每一层只能选择与这一层相连的某一层，所以后面对前面有影响，后面的确定了，前面的自然就确定了
    //从后往前遍历每一层，每次选出与这一层相连的能获得的价值最大的，也就是dp最大
    for (int i = n; i >= 1; i--) {
        int mx = 0;
        for (int j = 1; j <= a[i].c; j++) {
            mx = max(dp[a[i].l[j]], mx);
        }
        dp[i] = a[i].val + mx;
        ans = max(ans, dp[i]);
    }
    printf("%d\n", ans);
    return 0;
}

传球游戏

题目描述
上体育课时，墨老师经常带着同学们一起做游戏。这次，墨老师带着同学们一起做传球游戏，游戏规则是这样的：N个同学站成一个圆圈，其中的一个同学手里拿着一个球，当老师吹哨子时开始传球，每个同学可以把球传给自己左右的两个同学中的一个（左右任意），当老师再次吹哨子时，传球停止，此时拿着球没传出去的那个同学就是败者，要给大家表演一个节目。

聪明的张琪曼提出一个有趣的问题：有多少种不同的传球方法可以使得从张琪曼手里开始传的球，传了Ｍ次以后，又回到张琪曼手里。两种传球的方法被称作不同的方法，当且仅当这两种方法中，接到球的同学按接球顺序组成的序列是不同的。比如有3个同学1号、2号、3号，并假设张琪曼为1号，球传了3次回到张琪曼手里的方式有1à2à3à1和1à3à2à1，共两种。

输入
有两个用空格隔开的整数N，M（3≤N≤30，1≤M≤30）。

输出
有一个整数，表示符合题目的方法数。

样例输入
3 3
样例输出
2

AC代码

#include 

using namespace std;
int dp[33][33];//dp[i][j]表示传到第i个人传j次总的方法数 等于左边和右边传j-1次总的方法数的和

int main() {
#ifdef ONLINE_JUDGE
#else
    freopen("in.txt", "r", stdin);
#endif

    int n, m;
    scanf("%d%d", &n, &m);
    dp[1][0] = 1;//第一个人传0次传到第一个人手里的方法数为1
    for (int i = 1; i <= m; i++) {  //m次
        for (int j = 2; j < n; j++) {
            dp[j][i] = dp[j + 1][i - 1] + dp[j - 1][i - 1];
        }
        dp[1][i] = dp[2][i - 1] + dp[n][i - 1];
        dp[n][i] = dp[1][i - 1] + dp[n - 1][i - 1];
    }
    printf("%d\n", dp[1][m]);
    return 0;
}

黑熊过河

题目描述
晶晶的爸爸给晶晶出了一道难题：有一只黑熊想过河，但河很宽，黑熊不会游泳，只能借助河面上的石墩跳过去，它可以一次跳一墩，也可以一次跳两墩，但是每跳一次都会耗费一定的能量，黑熊最终可能因能量不够而掉入水中。所幸的是，有些石墩上放了一些食物，这些食物可以给黑熊增加一定的能量。问黑熊能否利用这些石墩安全地抵达对岸？请计算出抵达对岸后剩余能量的最大值。

输入
第1行包含两个整数P(黑熊的初始能量)，Q(黑熊每次起跳时耗费的能量)，0≤P,Q≤1000；
第2行只有一个整数n(1≤n≤106），即河中石墩的数目；
第3行有n个整数，即每个石墩上食物的能量值ai(0≤ai≤1000)。

输出
仅1行，若黑熊能抵达对岸，输出抵达对岸后剩余能量的最大值；若不能，则输出“NO”。

样例输入
12 5
5
0 5 2 0 7
样例输出
6
AC代码

#include 

using namespace std;
int a[1010];
int dp[1010];//dp[i]表示跳到第i个石头时最少消耗的能量，最后可以跳到n+1，即河对岸

int main() {
    int p, q;//初始能量 每次起跳时耗费的能量
    scanf("%d %d", &p, &q);
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    dp[0] = p;//没起跳时能量为p
    if (p >= q) {//判断第一次起跳能量够不够
        dp[1] = p + a[1] - q;
    } else {
        dp[1] = -1;//如果能量不够标记为-1
    }
    for (int i = 2; i <= n + 1; i++) {
        //每次起跳前判断这次起跳的能量够不够 即判断 dp[i - 1] >= q 和 dp[i - 2] >= q ，取可以跳到第i个位置的最大值，若跳不到就标记为-1
        dp[i] = max(dp[i - 1] >= q ? dp[i - 1] + a[i] - q : -1, dp[i - 2] >= q ? dp[i - 2] + a[i] - q : -1);
    }
    if (dp[n + 1] >= 0) {//n+1表示跳到了河对岸，判断到跳到河对岸时剩余的能量
        printf("%d\n", dp[n + 1]);
    } else {
        printf("NO\n");
    }
    return 0;
}

抢金块

题目描述
地面上有一些格子，每个格子上面都有金块，但不同格子上的金块有不同的价值，你一次可以跳S至T步(2≤S

输入
第1行是格子个数n (n<1000)；
第2行是S和T，保证T大于S(2≤S 第3行是每个格子上的金块价值Pi (Pi<10000)。

输出
输出最多可以获得的金块的总价值。

样例输入
10
2 3
4 5 8 2 8 3 6 7 2 9
样例输出
36

提示
样例说明：跳1、3、5、8、10，总价值：4+8+8+7+9=36。

AC代码

#include 

using namespace std;
int a[1024];
int dp[1024];//dp[i]表示从1开始跳到i个格子获得的金块的最大价值

int main() {
    int n, s, t;
    scanf("%d %d %d", &n, &s, &t);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    dp[1] = a[1];
    for (int i = 2; i <= n; i++) {
        for (int j = i - s; j >= i - t && j >= 1; j--) {//每次可以跳s到t步
            dp[i] = max(dp[i], dp[j] + a[i]);
        }
    }
    printf("%d\n", dp[n]);
    return 0;
}

维修栅栏

题目描述
农场的栅栏年久失修，出现了多处破损，晶晶准备维修它，栅栏是由n块木板组成的，每块木板可能已经损坏也可能没有损坏。晶晶知道，维修连续m个木板(这m个木板不一定都是损坏的)的费用是sqrt(m)。可是，怎样设计方案才能使总费用最低呢？请你也来帮帮忙。

输入
第1行包含一个整数n(n≤2500)，表示栅栏的长度；
第2行包含n个由空格分开的整数（长整型范围内）。如果第i个数字是0，则表示第i块木板已经损坏，否则表示没有损坏。

输出
仅包含一个实数，表示最小维修费用；注意：答案精确到小数点后3位。

样例输入
9
0 -1 0 1 2 3 0 -2 0
样例输出
3.000

AC代码

#include 

using namespace std;
int a[2510];
double dp[2510];//dp[i]表示修前i个所花的最少费用

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
    }
    dp[0] = 0;//初始化dp[0]为0，下面用到dp[0]，不修时费用为0
    for (int i = 1; i <= n; ++i) {
        if (a[i]) {//a[i]不为0时，所花最少费用为前一个花的费用
            dp[i] = dp[i - 1];
        } else {//a[i]为0时，加1表示维修这一个栅栏花费1
            dp[i] = dp[i - 1] + 1;
        }
        for (int j = 0; j < i; ++j) {//从0到i选出分成两块，前一部分(j之前的）为前面维修的最小花费 即dp[j]，后一部分(j之后的)为维修第i块的花费sprt(i-j)，选出最小值
            dp[i] = min(dp[i], dp[j] + sqrt(i - j));
        }
    }
    printf("%.3lf\n", dp[n]);
    return 0;
}

攀登宝塔

题目描述
有一天，贝贝做了一个奇怪的梦，梦中他来到一处宝塔，他想要从塔的外面爬上去。这座宝塔的建造特别，塔总共有n层，但是每层的高度却不相同，这造成了贝贝爬过每层的时间也不同。贝贝会用仙术，每用一次可以让他向上跳一层或两层，这时不会耗费时间，但是每次跳跃后贝贝都将用完灵力，必须爬过至少一层才能再次跳跃。贝贝想用最短的时间爬到塔顶，可是他找不到时间最短的方案，所以请你帮他找一个时间最短的方案，让他爬到塔顶（可以超过塔高）。贝贝只关心时间，所以你只要告诉他最短时间是多少就可以了。

输入
第1行一个数n (n≤10000)，表示塔的层数。
接下来的n行每行一个不超过100的正整数，表示从下往上每层的所需的时间。

输出
一个数，表示最短时间。

样例输入
5
3
5
1
8
4
样例输出
1

AC代码

#include 

using namespace std;
int a[2510];
int dp[2510][2];//dp[i][0]表示用法力 dp[i][1]表示不用法力

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
    }
    dp[1][0] = 0;
    dp[1][1] = a[1];
    for (int i = 2; i <= n; ++i) {
        dp[i][0] = min(dp[i - 1][1], dp[i - 2][1]);//登上第i层用法力等于前一层或两层用法力的最小值
        dp[i][1] = min(dp[i - 1][0] + a[i], dp[i - 1][1] + a[i]);//登上第i层不用法力等于前一层不用法力和前一层用法力的最小值 加上这一层消耗的时间
    }
    printf("%d\n", min(dp[n][0], dp[n][1]));
    return 0;
}

fstring字符串

题目描述
一个只包含A，B，C三种字符的字符串，如果其中有连续的3个由A，B，C各一个组成的子串，则称这个字符串为fstring字符串。
例如：BAACAACCBAAA就是一个fstring字符串，而AABBCCAABB则不是。
你的任务是计算只包含A，B，C三种字符且长度为n的这种字符串有多少个不是fstring字符串。

输入
一个整数n(l≤n≤30)。

输出
一个整数。

样例输入1
3
样例输出1
21
样例输入2
2
样例输出2
9

AC代码

#include 

using namespace std;
long long dp[33];

int main() {
    int n;
    long long cnt = 1;
    scanf("%d", &n);
    dp[1] = 3;
    dp[2] = 9;
    dp[3] = 21;
    for (int i = 4; i <= n; i++) {
        dp[i] = dp[i - 1] * 3 - dp[i - 2] - dp[i - 3];
    }
    printf("%lld\n", dp[n]);
    return 0;
}

防卫导弹

题目描述
一种新型的防卫导弹可截击多个攻击导弹。它可以向前或向下飞行，但不可以向后或向上飞行。它有一个缺点，尽管它发射时可以达到任意高度，但它只能截击比它上次截击导弹时所处高度低或者高度相同的导弹。现对这种新型防卫导弹进行测试，在每一次测试中，发射一系列的测试导弹，该防卫导弹所能获得的信息包括各进攻导弹的高度，以及它们的发射次序。求在每次测试中，该防卫导弹最多能截击的进攻导弹数量。

输入
第1行有若干个整数hi(0≤hi≤32767)，表示进攻导弹的高度，其中导弹数不超过4000个。

输出
一个整数，表示最多能截击的进攻导弹数。

样例输入
36 25 45 17 22 28
样例输出
3

AC代码

#include 

using namespace std;
int a[4002];
int dp[4002];//求最长不递增子序列的长度

int main() {
#ifdef ONLINE_JUDGE
#else
    freopen("in.txt", "r", stdin);
#endif
    int n = 0;
    int ans = 0;
    while (scanf("%d", &a[++n]) != EOF) {}
    n--;
    for (int i = 1; i <= n; ++i) {
        dp[i] = 1;
        for (int j = 1; j < i; ++j) {
            if (a[j] >= a[i]) {
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
        ans = max(ans, dp[i]);
    }
    printf("%d\n", ans);
    return 0;
}