机器学习实战笔记2——KNN及其实现

任务安排

1、机器学习导论       8、核方法
2、KNN及其实现      9、稀疏表示
3、K-means聚类      10、高斯混合模型
4、主成分分析          11、嵌入学习
5、线性判别分析      12、强化学习
6、贝叶斯方法          13、PageRank
7、逻辑回归              14、深度学习

KNN及其实现

Ⅰ 分类与聚类

      首先，我们先来区分下两个重要概念，分类与聚类
分类：
      事先已知道数据集中包含多少种类，从而对数据集中每一样本进行分类，且所分配的标签必须包含在已知的标签集中，属于监督学习。
聚类：
      将数据对象的集合分成相似的对象类（簇）的过程。使得同一类（簇）中的对象之间具有较高的相似性，而不同类（簇）中的对象具有较高的相异性，并且事先不知道数据集本身有多少类别，属于无监督学习。
      正所谓，物以类聚，人以群分，对于分类和聚类的应用也大相径庭
      分类应用：对一个学校的在校大学生进行性别分类，我们知道有且仅可分为“男”，“女”两类
      聚类应用：对于在校大学生，同学们根据自己的兴趣爱好等因素聚成 $n$ 个小团体
由此我们知道，分类与聚类：
不同点：
      分类已知种类个数与类型进行区分；
      聚类的种类个数与类型均未知；
共同点：
      分类与聚类的类中有很高相似性，类间有很高相异性

Ⅱ 定义

      KNN 算法，是数据挖掘分类技术中最简单的一种
      KNN（K-NearestNeighbor），K 最近邻分类算法，K 是指最近的 K 个邻居，而测试样本可以根据这 K 个邻居的特征值来代表，KNN 算法，就是通过测量不同特征值之间的距离来实现的

★Ⅲ 算法剖析

输入：训练样本 {$xi，yi$}${}_{i=1}^n$，测试样本 $x$，近邻个数 $K$，距离函数 $dist$
输出：测试样本的预测类别 $y$
      1.计算测试数据与各个训练数据之间的距离；
      2.按照距离的递增关系进行排序；
      3.选取距离最小的 K 个点；
      4.分别确定前 K 个点所在类别的出现频率；
      5.返回前 K 个点中出现频率最高的类别作为测试数据的预测分类；
（老师还给了个看着挺复杂的公式）

$$y\leftarrow \arg max\sum _{i=1}^K\delta (y,f(si)){(}_{y\in f(X)}$$

      记 $x$ 的 $K$ 个最近邻为 $S1、S2\dots \dots Sk$
      $f(X)$ 是类别映射函数
      脉冲函数 $\delta (x,y)$ 当且仅当 $x=y$ 时取1，其他为0
      通俗点理解，右边的 $\sum$ 函数是计数器，符合一类的+1，最终把最多的一类赋值给 $y$（即 $x$ 的预测类别）

Ⅳ 距离的求法

      分析了这么多，归根结底，KNN 算法的核心是求距离（即每个训练样本点与测试样本点之间的距离），下面介绍几种常见距离：

★1、欧几里得距离（Euclidean Distance）：

就是我们最常见的距离求法，衡量多维空间各点之间的绝对距离
$$dist(X,Y)=\sqrt{\sum _{i=1}^n(xi-yi{)}^2}$$

2、明可夫斯基距离（Minkowski Distance）：

明氏距离是欧氏距离的推广，是对多个距离度量公式的概括性表述，当p=2时即欧几里得距离
$$dist(X,Y)=(\sum _{i=1}^n|xi-yi{|}^p{)}^{1/p}$$

3、曼哈顿距离（Manhattan Distance）：

曼哈顿距离来源于城市区块距离，是将多个维度上的距离进行求和后的结果，是明氏距离中p=1的情况
$$dist(X,Y)=\sum _{i=1}^n|xi-yi|$$

4、向量空间余弦相似度（Cosine Similarity）：

（点乘公式的变形）余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上
$$sim(X,Y)=cos\theta =\frac{x\cdot y}{||x||\cdot ||y||}$$

Ⅴ 优缺点

      1.如上面方块三角的例子所示，当样本不平衡时，取的 K 不同，$y$ 的结果也不同，准确率也随之下降
      2.计算量大，尤其是特征数非常多的时候。
      3.KD 树，求树之类的模型建立需要大量的内存。
      4.是慵懒散学习方法，基本上不学习，导致预测时速度比起逻辑回归之类的算法慢。
      5.相比决策树模型，KNN 模型的可解释性不强。
（3、5点的例子我也不太懂，老师说后续课程会学到）

Ⅵ 分类精度

被正确分类的样本数占样本总数的个数
$$ACC=\frac{n_{correct}}{n_{total}}$$
例：
有一个用来对猫（cats）、狗（dogs）、兔子（rabbits）进行分类的系统
总共有 27 只动物：8 只猫， 6 条狗， 13 只兔子
混淆矩阵，是为了进一步分析性能而对该算法测试结果做出的总结
结果的混淆矩阵为：

$分类精度=（5+3+11）/27\approx 0.704$ （主对角线元素相加/总数）

Ⅶ 算法优化

（作了解即可）

1、距离加权最近邻算法：

对 KNN 的一个显而易见的改进是对 K 个近邻的贡献加权，根据它对相对查询点 $x_q$ 的距离，将较大的权值赋给较近的近邻。
$$\hat{f}(x)\leftarrow \arg \underset{y\in f(X)}{\max }\sum _{i=1}^k{\omega }_i\delta (y,f(xi))$$
很好理解，生活中肯定也是与你关系越好的朋友，与你相似度越高，越能代表你

2、回归（regression）最近邻算法

$$\hat{f}(x)\leftarrow \frac{{\sum }_{i=1}^{k}f(x_i)}{k}$$
上节课有提到过，回归用于连续型变量的预测，如经济走向等

3、加权回归最近邻算法

$$\hat{f}(x)\leftarrow \frac{{\sum }_{i=1}^k{\omega }_i\delta (y,f(xi))}{{\sum }_{i=1}^k{\omega }_i}$$
———————————————分割线———————————————
（算是明白了，老师就是只讲理论原理，代码实现让我们自个儿搞定，虽然挺锻炼能力的，但是着实很累啊！！！）

今日任务

1、Sklearn 中的 make_circles 方法生成训练样本，并随机生成测试样本，用KNN分类并可视化

2、Sklearn 中的 datasets 方法导入训练样本，并用留一法产生测试样本，用 KNN 分类并输出分类精度。[留一法：留一个样本进行测试，其它所有的用来训练，遍历所有样本]
            data = sklearn.datasets.iris.data
            label = sklearn.datasets.iris.target
3、下载 CIFAR图像数据集，并跑一下图像分类（选做）
4、颜值打分数据和模型下载

任务解决

1、这次没有完整的代码 copy 了，有点失落，只能借鉴下前辈写的类似的KNN 用法依样葫芦了
关键点：
①随机生成测试样本，那么横纵坐标分别用 random 得到（默认是0~1）
有可能会想到效仿代码第 8 行生成一个样本

x2, y2 = make_circles(n_samples=1, factor=0.5, noise=0.1)

实则不可取，这个生成的点是在两个圈上的随机，并非实质上的随机（无法在空白处生成点）；看见一个 make_blobs 函数，应该是可以用来生成单个随机点的，不过画图的时候数组取值要稍微注意下
②KNN实现

from sklearn.datasets import make_circles
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import numpy as np
import random

fig = plt.figure(1)
x1, y1 = make_circles(n_samples=400, factor=0.5, noise=0.1) 
# 模型训练 求距离、取最小K个、求类别频率
knn = KNeighborsClassifier(n_neighbors=15)
knn.fit(x1, y1)   # X是训练集(横纵坐标) y是标签类别
# 进行预测
x2 = random.random() # 测试样本横坐标
y2 = random.random() # 测试样本纵坐标

X_sample = np.array([[x2, y2]])   # 给测试点
y_sample = knn.predict(X_sample)   # 得预测类别
neighbors = knn.kneighbors(X_sample, return_distance=False)

plt.subplot(121)
plt.title('make_circles 1')
plt.scatter(x1[:, 0], x1[:, 1], marker='o', c=y1)
plt.scatter(x2, y2, marker='*', c='b')

plt.subplot(122)
plt.title('make_circles 2')
plt.scatter(x1[:, 0], x1[:, 1], marker='o', c=y1)
plt.scatter(x2, y2, marker='*', c='b')
for i in neighbors[0]:
    # plt.plot([x1[i][0], X_sample[0][0]], [x1[i][1], X_sample[0][1]], '-', linewidth=0.6, c='b')   连线
    plt.scatter([x1[i][0], X_sample[0][0]], [x1[i][1], X_sample[0][1]], marker='o', c='b', s=50)

plt.show()

效果图（如果觉得效果不好可以再多连个线）

本以为到这就算结束了，没想到老师让我们自己敲KNN的代码，不用Python 的库，行8，有点脑阔疼
放代码（效果无异，不过应该时间复杂度偏高）

from sklearn.datasets import make_circles
import matplotlib.pyplot as plt
import numpy as np
import random
import heapq

fig = plt.figure(1)
x1, y1 = make_circles(n_samples=400, factor=0.5, noise=0.1)
distance = []
k = 15
x2 = random.random()
y2 = random.random()

for i in range(0, 400):
    dx = x1[:, 0][i] - x2
    dy = x1[:, 1][i] - y2
    d = (dx**2+dy**2)**1/2
    distance.append(d)

min_index = map(distance.index, heapq.nsmallest(k, distance))
# 求最大的的k个数即用nlargest(此方法仅适用无重复情况，重复情况需改进)

plt.subplot(121)
plt.title('make_circles 1')
plt.scatter(x1[:, 0], x1[:, 1], marker='o', c=y1)
plt.scatter(x2, y2, marker='*', c='b')

plt.subplot(122)
plt.title('make_circles 2')
plt.scatter(x1[:, 0], x1[:, 1], marker='o', c=y1)
plt.scatter(x2, y2, marker='*', c='b')
for q in list(min_index):
    plt.scatter(x1[q, 0], x1[q, 1], marker='o', c='b', s=50)

plt.show()

补充一点numpy的知识

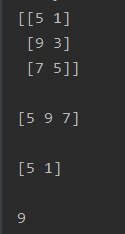
import numpy as np
x1 = np.array([[5, 1], [9, 3], [7, 5]])
print(x1)
print()
print(x1[:, 0], end="\n\n")
print(x1[0, :], "\n")
print(x1[:, 0][1])

输出结果

2、关键点：
①导入经典数据集鸢尾花iris
Iris 鸢尾花数据集是一个经典数据集，在统计学习和机器学习领域都经常被用作示例。数据集内包含 3 类共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这 4 个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica）中的某一品种。
②留一交叉验证
用 KNN 库

from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, LeaveOneOut
import matplotlib.pyplot as plt

iris = datasets.load_iris()

X = iris.data
y = iris.target
loo = LeaveOneOut()
# knn = KNeighborsClassifier(15)   # 默认k=5
# correct = 0

# for train, test in loo.split(X):
#     # print("留一划分：%s %s" % (train.shape, test.shape))
#     # X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.4, random_state=0)
#     knn.fit(X[train], y[train])
#     y_sample = knn.predict(X[test])
#     if y_sample == y[test]:
#         correct += 1
#
# print('Test accuracy:', correct/len(X))
K = []
Accuracy = []
for k in range(1, 16):
    correct = 0
    knn = KNeighborsClassifier(k)
    for train, test in loo.split(X):
        # print("留一划分：%s %s" % (train.shape, test.shape))
        # X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.4, random_state=0)
        # train_test_split 用于任意划分训练集与测试集 test_size是测试集百分比
        knn.fit(X[train], y[train])
        y_sample = knn.predict(X[test])
        if y_sample == y[test]:
            correct += 1
    K.append(k)
    Accuracy.append(correct/len(X))
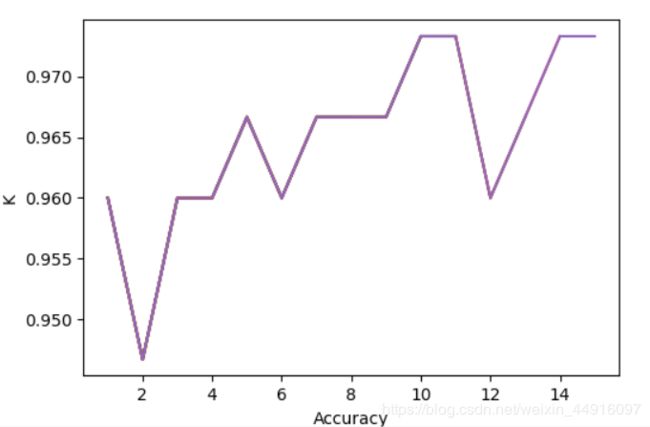
    plt.plot(K, Accuracy)
    plt.xlabel('Accuracy')
    plt.ylabel('K')
    print('K： ', k)
    print('Test Accuracy: ', correct/len(X))

plt.show()

效果图

顺便可视化了一下

有个实时可视化的画法，太久没写有点忘了，后续补

用自写 KNN，借鉴 knn算法(纯python实现)

from sklearn.model_selection import LeaveOneOut
import numpy as np
from sklearn import neighbors, datasets


def myknn(test, train, labels, k):
    # 返回所属类别
    m, n = train.shape   # shape(m, n)m列n个特征
    # 计算测试数据到每个点的欧式距离
    distances = []
    for i in range(m):
        sum = 0
        for j in range(n):
            sum += (test[j] - train[i][j]) ** 2
        distances.append(sum ** 0.5)

    sortDist = sorted(distances)
    # print(sortDist)
    # k 个最近的值所属的类别
    classCount = {}
    for i in range(k):
        voteLabel = labels[distances.index(sortDist[i])]
        classCount[voteLabel] = classCount.get(voteLabel, 0) + 1   # 0:map default
    sortedClass = sorted(classCount.items(), key=lambda d: d[1], reverse=True)
    return sortedClass[0][0]


k_neighbors = 15
iris = datasets.load_iris()
X = iris.data
y = iris.target
# print(data)
# print(label)
# print(classify(data[137], data, label, n_neighbors))

loo = LeaveOneOut()

correct = 0
for train_index, test_index in loo.split(X, y):
    # print("训练集:", train_index)
    # print("测试集为:", test_index[0])
    # print("X_train:", data[train_index])
    # print("X_test:", label[test_index])

    # 放在自己写的KNN跑结果
    if myknn(X[test_index[0]], X, y, k_neighbors) == y[test_index[0]]:
        correct += 1

    # print("正确数：", correct)
    # print("")

print('K: ', k_neighbors)
print("正确率为：", correct / len(X))

3、KNN 分类器进行图像分类——（降维方法）主成分分析PCA，线性判别分析LDA