VINS-Mono论文翻译

VINS-Mono源码PC版: https://github.com/HKUST-Aerial-Robotics/VINS-Mono
VINS-Mono源码ios版: https://github.com/HKUST-Aerial-Robotics/VINS-Mobile

摘要

一个摄像机和一个低成本惯性测量单元(IMU)构成了一个单目视觉惯性系统(VINS)，这是用于度量六自由度(DOF)状态估计的最小传感器套件(在尺寸、重量和功率方面)。在这篇文章，我们提出了VINS-Mono：一种鲁棒且通用的单目视觉惯性状态估计器。我们的方法从一个健壮的估计器初始化过程开始。采用一种基于紧耦合、非线性优化的方法，通过融合预积分后的IMU测量值和特征观测值，获得高精度的视觉惯性里程计。结合紧耦合方法，回环检测模块能够以最小的计算代价实现重定位。此外，我们还执行4自由度的位姿图优化，以加强全局一致性。更进一步，该系统可以通过一种有效的方法保存和加载地图来实现地图重用。通过全局位姿图优化，可以将当前和以前的地图融合在一起。我们在公共数据集和实际实验上验证了系统的性能，并与其他最先进的算法进行了比较。我们还在微型飞行器(MVP)平台上进行了机载闭环自主飞行，并将算法移植到基于ios的演示中。特别强调的是，本文提出的工作是一个可靠、完整和通用的系统，适用于需要高精度定位的不同应用。我们为PC和iOS移动设备开源了我们的实现方法。

关键词

单目视觉惯性系统（VINS），状态估计，传感器融合，SLAM

1.引言

  状态估计无疑是机器人导航、自主驾驶、虚拟现实和增强现实(AR)等广泛应用中最基本的模块。由于单目相机体积小、成本低、硬件设置简单，仅使用单目摄像机的方法获得了社会的极大兴趣。然而，单目视觉系统无法恢复度量尺度，因此限制了它们在机器人中的实际应用。近年来，利用低成本惯性测量单元(IMU)辅助单目视觉系统的发展趋势日益明显。这种单目视觉惯性系统(VINS)的主要优点是具有可观测的度量尺度，以及翻滚角(roll)和俯仰角(pitch)。这让需要有尺度的状态估计的导航任务成为可能。此外，对IMU测量值的积分可以通过弥补由于光照变化、无纹理区域或运动模糊造成的视觉轨迹损失，显著提高运动跟踪性能。单目VINS不仅广泛应用于地面机器人和无人机上，也可应用于移动设备上。对自我和环境感知而言，它在尺寸、重量、功耗等方面都有很大的优势。
  但是，有几个问题影响了单目VINS的使用。第一个是严格的初始化。由于缺乏直接的距离测量，很难直接将单目视觉结构与惯性测量融合。同时，我们也认识到VINS是高度非线性的，因此在估计器初始化方面我们遇到了重大的挑战。在大多数情况下，系统应该从一个已知的静止位置启动，并在开始时缓慢而小心地移动，这限制了它在实践中的使用。另一个问题是视觉惯性里程计 (VIO)的长期漂移是不可避免的。为了消除漂移，必须进行回环检测、重定位和全局优化。除了这些关键问题之外，对地图保存和重用的需求还在增长。
  为了解决这些问题，我们提出了一种鲁棒的、通用的单目视惯性状态估计器VINS-Mono，这是我们之前三部作品[6]-[8]的结合和延伸。VINS-Mono包含以下特性：
　　**1)**鲁棒的初始化过程，能够从未知的初始状态引导系统。
　　**2)**基于优化的紧耦合单目VIO，包括相机与IMU的外参标定以及IMU偏移矫正。
　　**3)**在线重定位和4自由度(DOF)全局位姿图优化
　　**4)**位姿图重用，可以保存、加载和融合多个局部位姿图。
  在这些特性中，鲁棒的初始化、重定位和位姿图重用是我们的技术贡献，它们来自于我们之前的工作[6]-[8]。工程方面的贡献包括开源系统集成、无人机导航的实时演示和移动应用程序。整个系统已经被成功应用于小规模AR场景，中型无人机导航和大规模状态估计任务，如图1所示。
　　　　　　　　
　　　　　　　　　　　　(a) 轨迹(蓝色)和特征位置(红色)
　　　　　　　　
　　　　　　　　　(b) 轨迹覆盖与用于可视化比较的谷歌地图
　　　　　　
　　　　　　　　图1 单目视觉惯性状态估计器的室外实验结果

  在正常行走条件下，采用手持式单目摄像机imu采集数据。它包括两个完整的圆圈内的领域和两个半圆形附近的车道。轨迹总长度为2.5 km。实验视频可以在多媒体附件中找到。
  本文其余部分的结构如下。在第二部分中，我们讨论了相关的文献。在第三部分中，我们概述了整个系统的框架。在第四部分中，给出了视觉的预处理和IMU测量值的预积分步骤。在第五部分中，我们讨论了估计器的初始化过程。在第六部分中，提出了一种紧耦合、自标定、非线性优化的单目VIO。在第七部分中，提出了紧耦合重定位。在第八部分中，讨论了全局位姿图优化和重用。在第九部分中，展示了实验结果。最后，在第十部分中，本文对未来可能的研究方向进行了探讨和展望。

2.相关工作

  基于单目视觉的状态估计/里程计/SLAM方面的学术著作非常广泛。值得注意的方法包括PTAM[1]、SVO[2]、LSD-SLAM[3]、DSO[5]和ORB-SLAM[4]。显然，任何给出完整的相关回顾的尝试都是不完整的。然而，在本节中，我们跳过了关于纯视觉方法的讨论，只关注与单目视觉惯性状态估计最相关的结果。
  处理视觉和惯性测量最简单的方法是松耦合的传感器融合[9]，[10]，其中IMU作为一个独立的模块来辅助视觉结构。融合通常由扩展卡尔曼滤波器(EKF)完成，其中IMU用于状态传播，而视觉位姿用于更新。进一步说，紧耦合视觉惯性算法要么基于EKF[11]-[13]，要么基于图优化[14]-[19]，其中相机和IMU测量值是从原始测量水平联合优化的。一个流行的基于EKF的VIO方法是MSCKF [11]，[12]。MSCKF在状态向量中维护以前的多个摄像机姿态，并使用多个摄像机视图中相同特征的视觉测量来形成多约束更新。SR-ISWF[20][21]是MSCKF的扩展。它采用平方根形式[14]实现单精度表示，避免了较差的数值性质。该方法采用逆滤波器进行迭代再线性化，与基于优化的算法等价。批量图优化或集束调整技术（BA）维护和优化所有测量值以获得最优状态估计。为了实现恒定的处理时间，基于图的VIO方法[15]、[17]、[18]通常通过边缘化过去的状态和测量值来优化最近状态的有界滑动窗口。由于非线性系统迭代求解的计算要求较高，很少有基于图的方法能够在移动电话等资源受限的平台上实现实时性。
  对于视觉测量处理，根据残差模型的定义，可以将算法分为直接法和间接法。直接法[2]，[3]，[22]最小化光度误差，而间接法[12]，[15][17]最小化几何位移。直接方法由于其吸引区域小，需要良好的初始估计，而间接方法在提取和匹配特征方面消耗额外的计算资源。由于其成熟度和鲁棒性，间接方法在实际工程应用中更常见。然而，直接法更容易扩展到稠密建图，因为它们是直接在像素级别上操作的。
  IMU通常以比摄像机更高的速率获取数据。不同的方法被提出来处理高速率的IMU测量值。最直接的方法是在基于EKF的方法中使用IMU进行状态传播[9][11]。在图优化公式中，为了避免重复的IMU积分，提出了一种有效的方法，即IMU预积分(IMU pre-integration)。该技术在文献[23]中首次被提到，它使用欧拉角参数化旋转误差。Shen等人利用连续时间误差状态动力学推导了协方差传递方程。在[19]和[24]中，通过加入后验IMU偏置校正，进一步完善了积分理论。
  精确的初始值对于引导任何单目VINS都是至关重要的。在[17]和[25]中提出了一种利用短期IMU预积分相对旋转的线性估计初始化方法。该方法不能对原始投影方程中的陀螺偏差和图像噪声进行建模。在[26]中介绍了单目视觉惯性初始化问题的一种封闭形式解决方案。后来，在[27]中提出了通过增加陀螺仪偏差校准来扩展这种封闭形式解决方案。这些方法无法对惯性积分的不确定性进行建模，因为它们依赖于长时间内IMU测量值的双重积分。在[28]中，提出了一种基于SVO[2]的重新初始化和故障恢复算法。需要一个额外的向下的距离传感器来恢复尺度。在[18]中引入了一种建立在流行的ORB-SLAM[4]之上的初始化算法。据研究，其尺度收敛所需的时间超过10秒。这可能会给需要在一开始就进行规模评估的机器人导航任务带来问题。
  VIO方法，不管它们所依赖的基本数学公式是什么，在全局的平移和旋转中长期受到漂移的影响。为此，回环检测在长期操作中起着重要的作用。ORBSLAM[4]能够闭合回环并重用地图，它利用了词袋模型[29]。一个7自由度[30]的(位置，方向和尺度)位姿图优化遵循回环检测。

3.概述

  所提出的单目视惯性状态估计器的结构如图2所示。该系统从测量预处理(参见第四部分)开始，在预处理过程中提取和跟踪特征，对两个连续帧间的IMU测量值进行预积分。初始化过程(参见第五部分)提供了所有必要的值，包括姿态、速度、重力向量、陀螺仪偏差和三维(3-D)特征位置，用于引导后续基于非线性优化的VIO。VIO(参见第六部分)与重定位(参见第七部分)模块紧密地融合了预积分的IMU测量和特征观测。最后，位姿图优化模块((参见第八部分)接受几何验证的重定位结果，并进行全局优化以消除漂移。实现了位姿图的重用。VIO和位姿图优化模块在单独的线程中并行运行。

　　　　　　　　　　　　　　　　　图2 所提出的单目VINS的完整传递框图

  与最先进的适用于双目相机的VIO算法OKVIS[15]相比，我们的算法是专门为单目相机设计的。因此，我们特别提出了一个初始化过程，关键帧选择标准。并且为了更好地跟踪性能，使用操作了一个大视场(FOV)相机。此外，我们的算法提出了一个带有闭合回环和位姿图重用模块的完整系统。
  现在，我们定义了贯穿本文的符号和坐标系定义。我们认为$(\cdot {)}^w$是世界坐标系(world frame)。重力的方向与世界坐标系的$z$轴对齐。$(\cdot {)}^b$是本体坐标系(body frame)，我们把它定义为与IMU坐标系相同。$(\cdot {)}^c$是相机坐标系(camera frame)。我们使用旋转矩阵$R$和Hamilton四元数$q$来表示旋转。我们主要在状态向量中使用四元数，但也用旋转矩阵表示三维向量的旋转。$q_b^w$和$p_b^w$表示从本体坐标系到世界坐标系的旋转和平移。$b_k$表示获取第k个图像时的本体坐标系。$c_k$表示获取第k个图像时的相机坐标系。⊗代表了两个四元数乘法操作。世界坐标系中的重力向量为$g^w=[0,0,g{]}^T$。最后，我们将(^)表示为某一具体量的噪声测量值或估计值。

4.测量预处理

  本节介绍惯性和单目视觉测量的预处理步骤。对于视觉测量，我们跟踪连续帧之间的特征，并检测最新帧中的新特征。对于IMU测量，我们在两个连续的帧之间对它们进行预积分。

A.视觉处理前端

  对于每一幅新图像，利用KLT稀疏光流算法对现有的特征点进行跟踪[31]。同时，检测新的角点特征[32]以保证每幅图像特征的最小数目(100-300)。该检测器通过在两个相邻特征之间设置最小像素间隔来执行均匀的特征分布。二维特征首先是不失真的，然后在通过外点剔除后投影到一个单位球面上。使用基本矩阵模型的RANSAC算法[33]进行外点剔除。
  在此步骤中还将选择关键帧。我们有两个关键帧选择标准。第一个是与上一个关键帧的平均视差。如果在当前帧与最新关键帧之间被跟踪特征点的平均视差超过一定阈值，则将该帧视为新的关键帧。请注意，不仅平移，旋转也会产生视差。然而，特征点无法在纯旋转运动中三角化。为了避免这种情况，我们在计算视差时使用陀螺仪测量值的短期积分来补偿旋转。注意，这种旋转补偿仅用于关键帧选择，而不涉及VINS公式中的旋转计算。为此，即使陀螺仪存在较大的噪声或偏置，也只会产生次优的关键帧选择结果，不会直接影响估计质量。另一个标准是跟踪质量。如果跟踪的特征数量低于某个阈值，我们将该帧视为一个新的关键帧。这个标准是为了避免完全丢失特征轨迹。

B.IMU预积分

  我们遵循我们之前基于连续时间四元数的IMU预积分[16]的推导，并包括了对IMU偏置的处理，如[19]和[24]。我们注意到我们当前的IMU预积分过程与[19]和[24]的数值结果几乎相同，但使用了不同的推导方法。所以，我们在这里只做一个简单的介绍。关于基于四元数的推导的详细信息可以在附录A中找到。
  1) IMU噪声与偏置: IMU测量值是在机体坐标系内测量的，它是平衡重力和平台动力的合力，受加速度偏置$b_a$、陀螺仪偏置$b_w$和加性噪声的影响。原始的陀螺仪和加速度计测量值$\hat{w}$和$\hat{a}$，被给出：
　　　　　　　　　　　
  我们假设加速度、陀螺仪测量的加性噪声是高斯白噪声，$n_a\sim N(0,{\sigma }_a^2)$，$n_w\sim N(0,{\sigma }_w^2)$。加速度计偏置和陀螺仪偏置被建模为随机游走，其导数为高斯白噪声，$n_{b_a}\sim N(0,{\sigma }_{b_a}^2)$，$n_{b_w}\sim N(0,{\sigma }_{b_w}^2)$。
　　　　　　　　　　　
  2)预积分: 对于连续两帧$b_k$和$b_{k+1}$，在时间间隔内$[b_k,b_{k+1}]$内存在多个惯性测量值。给出了偏置估计值后，将它们从局部坐标系$b_k$下进行积分
　　　　　　　　　　　
这里，
　　　　　　　
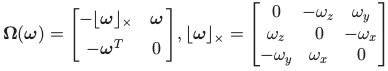
$\alpha ,\beta ,\gamma$的协方差$P_{b_{k+1}}^{b_k}$也相应的传递。可以看出，以$b_k$为给定偏置的参照系，仅用IMU测量值就可以得到如公式(3)所示的预积分项。
  3)偏差纠正: 如果估计偏置变化小,我们根据偏置调整，${\alpha }_{b_{k+1}}^{b_k}$，${\beta }_{b_{k+1}}^{b_k}$，${\gamma }_{b_{k+1}}^{b_k}$的一阶近似值，如
　　　　　　　　　　　
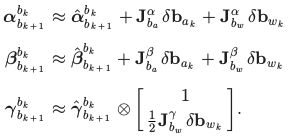
否则，当偏差估计发生显著变化时，我们在新的偏差估计下进行重新传播。这种策略为基于优化的算法节省了大量的计算资源，因为我们不需要重复传播IMU测量值。

5.估计器初始化

  单目紧耦合VIO是一个高度非线性的系统，需要在一开始就进行准确的初始化估计。通过将IMU预积分与纯视觉结构进行松耦合对齐，我们得到了必要的初始值。

A.滑动窗口(Sliding Window)纯视觉SfM

  初始化过程从纯视觉SfM估计相机尺度位姿(up-to-scale)和特征位置图开始。我们在一个滑动窗口中维护多个帧，以满足有限的计算复杂度。首先，我们检查最新帧和所有之前帧之间的特征对应。如果我们能在滑动窗口中的最新帧和任何其他帧之间，找到稳定的特征跟踪(超过30个跟踪特征)和足够的视差(超过20个像素)，我们使用五点算法[34]恢复这两帧之间的相对旋转和尺度平移。然后，我们任意设置尺度，并对这两帧中观察到的所有特征进行三角化。基于这些三角化的特征，采用PnP[35]来估计窗口中所有其他帧的位姿。最后，应用全局光束平差法(BA)[36]最小化所有特征观测值的总重投影误差。由于我们还没有任何关于世界坐标系的知识，所以我们将第一个相机坐标系$(\cdot {)}^{c_0}$设置为SfM的参考坐标系。所有帧的位姿$({\overline{p}}_{c_k}^{c_0},q_{c_k}^{c_0})$和特征位置表示都是相对于坐标系$(\cdot {)}^{c_0}$的。给定相机与IMU之间的外部参数$(p_c^b,q_c^b)$，可以将相机帧坐标系下的位姿转换为本体坐标系 (IMU帧) 下的位姿，如
　　　　　　　　　　　　　　　
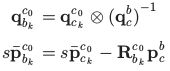
其中s为未知尺度参数，将在下一节中求解。

B.视觉惯性校准

  视觉惯性对准的示意图如图3所示，其基本思想是将尺度视觉结构与IMU预积分匹配。
　　　　　　　　
　　　　　　　　　　　　　图3 估计器初始化的视觉惯性对准过程演示
  1)陀螺仪偏置标定: 考虑窗口内连续两帧$b_k$和$b_{k+1}$，从视觉SfM中得到旋转$q_{b_k}^{c_0}$和$q_{b_{k+1}}^{c_0}$，从IMU预积分得到相对约束${\hat{\gamma }}_{b_{k+1}}^{b_k}$。我们将IMU预积分项相对于陀螺仪的偏置进行线性化，并最小化以下代价函数:
　　　　　　　　　　　　　
其中B代表窗口中所有帧的索引。通过这种方法，我们得到了陀螺仪偏置$b_w$的初始标定结果。然后，我们用新的陀螺仪偏置重新传递所有的IMU预积分项${\hat{\alpha }}_{b_{k+1}}^{b_k}$，${\hat{\beta }}_{b_{k+1}}^{b_k}$，${\hat{\gamma }}_{b_{k+1}}^{b_k}$。
  2)速度、重力矢量、尺度初始化: 陀螺仪偏置初始化后，我们继续初始化导航的其他必要状态，即速度、重力矢量、尺度。
　　　　　　　　　　　　　　
其中$V_{b_k}^{b_k}$为拍摄第k帧图像时在本体坐标系下的速度，$g^{c_0}$为$c_0$坐标系下的重力矢量，s是单目SfM到公制单位的尺度。
  考虑到窗口中连续的两帧$b_k$和$b_{k+1}$，我们有如下等式:
　　　　　　　　　　
我们可以将(6)和(9)合并成以下线性测量模型:
　　　　　　　　　
这里，
　　　　　　　　　　
可以看出$R_{b_k}^{c_0}$，$R_{b_{k+1}}^{c_0}$，${\overline{p}}_{c_k}^{c_0}$和${\overline{p}}_{c_{k+1}}^{c_0}$是从带尺度的单目视觉中得到的，$\nabla t_k$是连续两帧之间的时间间隔。通过求解线性最小二乘问题：
　　　　　　　　　　　　　　　　　
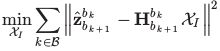
我们可以得到窗口中每一帧的本体坐标系速度，视觉参照系$(\cdot {)}^{c_0}$中的重力向量，以及尺度参数。
  3)重力细化: 通过约束大小，可以细化之前线性初始化步骤得到的重力向量。在大多数情况下，重力矢量的大小是已知的。这导致重力矢量只剩下2个自由度。因此，我们在其切线空间上用两个变量扰动重力，使其保持2自由度。扰动将重力向量表示为$g(\overline{\hat{g}}+\delta g)$，$\delta g=w_1{b}_1+w_2{b}_2$，其中$g$是已知的重力大小。$\overline{\hat{g}}$是表示重力方向的单位矢量。$b_1$和$b_2$是跨越正切平面的两个正交基，如图4所示。$w_1$和$w_2$分别为$b_1$和$b_2$上的对应位移。我们可以任意在正切空间中找到任何一组和。然后，我们用$g(\overline{\hat{g}}+\delta g)$代替$g$，解出二维向量$\delta g$和其它状态变量。这个过程需要迭代几次，直到$\overline{\hat{g}}$收敛(由于重力的大小已知，$g$位于半径$g\approx 9.81m/s^2$的球体上)。
　　　　　　　　　　
　　　　　　　　　　　图4 2自由度重力扰动图解
   4)完成初始化: 细化重力矢量后，通过将重力旋转到$z$轴上，我们能得到世界坐标系与摄像机坐标系$c_0$之间的旋转$q_{c_0}^w$。然后我们将所有变量从参考系$(\cdot {)}^{c_0}$旋转到世界坐标系$(\cdot {)}^w$。本体坐标系的速度也将被旋转到世界坐标系。视觉SfM的平移分量将被缩放到公制单位。此时，初始化过程已经完成，所有这些度量值都将被输入到一个紧耦合的单目VIO中。

6. 紧耦合单目VIO

   在估计器初始化之后，我们使用一个基于滑动窗口的紧耦合单目VIO进行高精度和鲁棒的状态估计。滑动窗口的阐述正如图5所示。在滑动窗口中存在多个摄像机姿态、IMU测量和视觉测量。它是一个带有IMU、视觉和回环测量的紧耦合阐述。
　　　
　　　　　　　　　图5 带有重新定位的单目VIO滑动窗口的图解

A.公式

   滑动窗口中的全状态向量被定义为：
　　　　　　　　　　
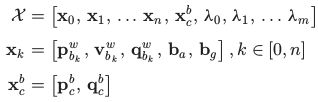
其中，$X_k$是捕获第k帧图像时的IMU状态。它包含了IMU在世界坐标系下的位置、速度和方向，以及在IMU本体坐标系下的加速度计偏置和陀螺仪偏置。$n$是关键帧的总数，$m$是滑动窗口中的特征总数，${\lambda }_l$是第一次观测到第$l$个特征的逆深度。
  我们使用视觉惯性BA。我们最小化所有测量残差的先验和Mahalanobis范数之和，得到最大后验估计：
　　　　　　　　　
其中Huber范数[37]被定义为：
　　　　　　　　　　　　　
$r_B({\hat{z}}_{b_{k+1}}^{b_k},\chi )$和$r_C({\hat{z}}_l^{c_j},\chi )$分别是IMU和视觉测量的残差。残差的详细定义将在第六节的B和C中提出。B是所有IMU测量的集合，C是在当前滑动窗口中至少观察到两次的一组特征。$\left\{r_p,H_p\right\}$是来自边缘化的先验信息。Ceres求解器[38]被用来求解这个非线性问题。

B.IMU测量残差

  考虑滑动窗口中连续两帧$b_k$和$b_{k+1}$内的IMU测量，预积分IMU测量的残差可以定义为：
　　　　　　　　　
其中，$[\cdot {]}_{xyz}$是提取四元数$q$的向量部分，以进行误差状态表示。$\delta {\theta }_{b_{k+1}}^{b_k}$是四元数的三维误差状态表示。 $[{\hat{\alpha }}_{b_{k+1}}^{b_k}$，${\hat{\beta }}_{b_{k+1}}^{b_k}$，${\hat{\gamma }}_{b_{k+1}}^{b_k}]$是两个连续图像帧间的IMU测量值的预积分项。加速度计和陀螺仪偏置也包括在在线校正的剩余项中。

C.视觉测量残差

  与传统的针孔相机模型在广义像面上定义重投影误差不同，我们定义了相机在单位球面上的测量残差。几乎所有类型相机的光学，包括广角相机、鱼眼相机或全向相机，都可以建模为连接单位球面表面的单位射线。考虑第$i$幅图像中第一次观测到的第$l$个特征，定义第 $j$幅图像中该特征观测的残差为：
　　　　　　　　　　　　　
其中，$[{\hat{u}}_l^{c_i},{\hat{v}}_l^{c_i},]$是在第$i$幅图像中第一次观测到的第$l$个特征。是在第$j$幅图像中对相同特征的观察。${\pi }_c^{-1}$是利用摄像机内参将像素位置转换成单位向量的反投影函数。由于视觉残差的自由度为2，我们将残差向量投影到正切平面上。如图6所示，$b_1$和$b_1$是在正切平面${\hat{\overline{p}}}_l^{c_j}$上的两个任意选择的正交基。：(14)中使用的方差$p_l^{c_j}$也从像素坐标传播到单位球面上。　
　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　图6 在单位球面上的视觉残差图解

D.边缘化

  为了限制基于优化的VIO的计算复杂度，引入了边缘化。我们有选择地从滑动窗口中将IMU状态$X_k$和特征${\lambda }_l$边缘化，同时将对应于边缘状态的测量值转换为先验。
  正如图7所示，当第二个最新帧是一个关键帧时，它将留在窗口中，而最老的帧与其相应的测量值将被边缘化。但如果第二个最新帧是一个非关键帧，我们丢掉视觉测量值，保留连接到这个非关键帧的IMU测量值。为了保持系统的稀疏性，我们不会边缘化非关键帧的所有测量值。我们的边缘化方案的目的是在窗口中保持关键帧的空间分隔。这确保了特征三角化有足够的视差，并且最大化了在大激励下获得加速度计测量值的可能性。
　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　图7 边缘化策略图解
　　边缘化是利用Schur补[39]进行的。我们基于所有与被移除状态相关的边缘化测量值构建了一个新的先验。新的先验项被添加到现有的先验项中。我们注意到边缘化导致线性化点的早期固定，这可能导致次优估计结果。但是，由于VIO可以接受小的漂移，所以我们认为边缘化带来的负面影响并不严重。

E.摄像机速率状态估计的纯运动视觉惯性BA

  对于手机等计算能力较低的设备，由于非线性优化计算量较大，紧耦合的单目VIO无法实现相机速率的输出。为此，在充分优化的基础上，我们采用了一种轻量级的纯运动视觉惯性优化，将状态估计提高到相机速率(30Hz)。
  纯运动视觉惯性优化的代价函数与(14)中单目VIO的代价函数相同。然而，我们并没有优化滑动窗口中的所有状态，而是只优化了固定数量的IMU最新状态的姿态和速度。我们将特征深度、外部参数、偏置和不希望优化的旧IMU状态视为常量。我们确实使用了所有的视觉和惯性测量来进行纯运动的优化。这使得状态估计比单帧PnP方法更平滑。图8给出了该策略的图解。与在最先进的嵌入式计算机上可能导致超过50ms的完全紧耦合单目VIO相比，这种纯运动的视觉惯性优化大约只需5ms来计算。这使得低延迟的相机频率进行位姿估计对无人机和AR应用特别有利。
　　　　　　　　　　
　　　　　　　　　　　　　图8 相机速率级输出的纯运动优化图解

F.IMU前向传递以达到IMU速率状态估计

  IMU测量的速率比视觉测量高得多。虽然我们的VIO频率受到图像捕获频率的限制，但是我们仍然可以用最近的IMU测量直接传播最新的VIO估计来实现IMU速率级的性能。高频状态估计可以作为回环检测的状态反馈。利用这种IMU速率状态估计进行的自主飞行实验在第九节的C中给出。

7. 重定位

  我们的滑动窗和边缘化方案限制了计算复杂度，但也为系统引入了累积漂移。为了消除漂移，提出了一种与单目VIO无缝集成的紧耦合重定位模块。重定位过程从一个回环检测模块开始，该模块识别已经访问过的位置。然后建立回环检测候选帧和当前帧之间的特征级连接。这些特征的对应关系紧密地集成到单目VIO模块中，以最小的计算量获得无漂移状态估计。多特征的多次观测直接用于重定位，具有较高的精度和较好的状态估计平滑性。重定位过程如图9(a)所示。
　　　　　　　　　
　　　　　　　　　　　　　图9 重定位和位姿图优化过程图示
　　 (a)重新定位过程。它开始于纯VIO的姿态估计(蓝色)。记录过去的状态(绿色)。如果最新的关键帧检测到一个回环(参见第7节的A)，如第2幅图中的红线所示，则发生了重新定位。注意，由于使用了特征级对应关系进行重新定位，我们能够合并多个来自过去关键帧的回环检测约束(参见第7节的C)，如后三个图所示。

A.回环检测

  我们利用DBoW2[29]，一种最先进的词袋位置识别方法来进行回环检测。除了用于单目VIO的角点特征外，另外500个角点被检测并由BRIEF描述子[40]描述。额外的角点特征用于在回环检测中实现更好的召回率。描述子被视为查询视觉数据库的视觉单词。DBoW2在时间和空间一致性检查后返回回环检测候选帧。我们保留所有用于特征检索的BRIEF描述子，丢弃原始图像以减少内存消耗。

B.特征恢复

  当检测到一个回环时，通过恢复特征对应关系，建立局部滑动窗口与闭环候选帧之间的连接。通过BRIEF描述子匹配找到对应关系。描述子匹配可能会导致一些误匹配对。为此，我们使用了两步进行几何异常值剔除，如图10所示。(a) BRIEF描述子匹配结果。(b)第一步操作:2D – 2D异常值剔除结果。©第二步操作:3D – 2D异常值剔除结果。
　　　　　　　　　
　　　　　　　图10 为了特征恢复，在回环闭合时进行描述子匹配和异常值去除
　　1)2D- 2D: RANSAC[33]的基本矩阵检验。我们利用当前图像和回环候选图像中恢复的特征二维观测进行基本矩阵检验。
　　2)3D- 2D: RANSAC[35]的PnP检验。基于特征在局部滑动窗口中已知的三维位置，以及回环候选图像中的二维观测值，进行PnP检验。
剔除外点后，我们将此候选帧视为正确的回环检测并执行重定位。

C.紧耦合重定位

重定位过程有效地将当前滑动窗口与过去的姿态对齐。在重定位过程中，我们将所有闭环帧的位姿都视为常量。我们使用所有的IMU测量值，局部视觉测量值和恢复的特征对应关系，共同优化滑动窗口。我们可以轻松地为闭合回环帧观察到的恢复特征编写视觉测量模型，使其与VIO中的视觉测量相同，如公式(17)所示。唯一的区别是，从位姿图(见第8节)或直接从上一个里程计的输出（如果这是第一次重定位）获得的回环帧的姿态$({\hat{q}}_v^w,{\hat{p}}_v^w)$被视为常数。为此，我们可以稍微修改(14)中的非线性代价函数，附加回环项为：
　　 　　　　　　　　　　
其中L为闭环帧中恢复的特征的观测集。$(l,v)$表示在闭环帧$v$中观察到的第$l$个特征。注意，虽然代价函数与(14)稍有不同，但是待解状态的维数是相同的，因为回环帧的位姿被视为常量。当使用当前滑动窗口建立多个闭合回环时，我们同时使用来自所有帧的所有闭环特征对应关系进行优化。这为重定位提供了多视图约束，从而获得更高的精度和更好的平滑性。第8节将讨论重定位后保持一致性的全局优化。

8. 全局位姿图优化和地图重用

  重定位后，将进行额外的位姿图优化步骤，以确保将过去的位姿集合注册到全局一致的配置中。

A.四个累积漂移方向

  由于重力惯性测量的好处，横滚角和俯仰角是完全可以观测到的。如图11所示，随着物体的运动，三维位置和旋转相对于参照系发生变化。然而，我们可以通过重力矢量来确定水平面，这意味着我们可以一直观察到绝对的横滚角和俯仰角。因此，横滚和俯仰是世界坐标系中的绝对状态，而$(x,y,z)$和偏航是相对于参考系的相对估计。累积漂移只发生在$(x,y,z)$和偏航角中。为了充分利用有效的信息，有效地校正漂移，我们对无漂移横滚和俯仰进行了修正，只进行了四自由度的位姿图优化。
　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　图11 四个漂移方向的图解

B.在位姿图中添加关键帧

  关键帧在VIO处理之后添加到姿态图中。每个关键帧作为位姿图中的一个顶点，通过两种类型的边与其他顶点连接，如图12所示。
　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　图12 位姿图说明　　
  1) 顺序边(Sequential Edge): 关键帧与之前的关键帧建立若干条顺序边。顺序边表示直接从VIO获取的两个关键帧之间的相对转换。考虑到关键帧$i$及其先前的一个关键帧$j$，顺序边只包含相对位置${\hat{p}}_{ij}^i$和偏航角${\hat{\psi }}_{ij}$。
　　　　　　　　　　　　　　　　　
　　2) 回环边(Loop Closure Edge)：如果关键帧有一个回环连接，则它通过位姿图中的回环边连接闭合回环帧。同样，回环边只包含一个与(19)定义相同的4自由度相对位姿变换。回环边的值由重定位结果得出。

C. 4自由度位姿图优化

  我们将帧$i$和$j$之间边的残差定义为：
　　 　　　　　　　　　
其中，${\hat{\varphi }}_i$和${\hat{\theta }}_i$是从单目VIO获得的横滚和俯仰角的合理估计。　
　　通过最小化以下代价函数，对顺序边和回环边的整个图进行优化：
　　　　　　　　　　　　　　
其中，S是所有顺序边的集合，L是回环边的集合。虽然紧耦合的重定位已经有助于消除错误的回环, 但我们添加了另一个Huber范数$\rho (\cdot )$ ，进一步减少任何可能的错误回环的影响。相反，我们不对顺序边使用任何鲁棒范数，因为这些边是从VIO中提取出来的，VIO已经包含了足够多的外点剔除机制。位姿图的优化和重定位(见第7节的C)在两个单独的线程中异步运行。这使得在最优化的位姿图可用时，可以立即使用它进行重新定位。同样，即使当前的位姿图优化尚未完成，仍然可以使用已有的位姿图配置进行重定位。这一过程如图9(b)所示。
　　(b)全局位姿图优化。当一个关键帧从滑动窗口被边缘化时，它被添加到位姿图中。如果在这个关键帧和任何其他过去的关键帧之间有一个回环，则表示为4自由度相对刚体变换的闭环约束也将添加到位姿图。使用所有相关的位姿约束在一个单独的线程中对位姿图进行优化(见第7节的C)，重定位模块总是根据最新的位姿图配置运行。

D.位姿图管理

该位姿图不仅可以优化当前地图，而且可以将当前地图与以前构建的地图合并。如果我们加载了一个以前构建的地图并检测到两个地图之间的回环连接，我们就可以将它们合并在一起。由于所有的边都是相对约束条件，因此位姿图优化通过回环连接自动将两个地图合并在一起。如图13所示，通过回环边将当前地图拉到之前的地图中。每个顶点和每条边都是相对变量。因此，我们只需要固定位姿图中的第一个顶点。黄色的图形是之前构建的地图。蓝色的图是当前的地图。根据回环连接合并两个地图。
　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　图13 地图合并说明

E.位姿图保存

我们的姿态图的结构非常简单。我们只需要保存顶点和边，以及每个关键帧(顶点)的描述子。原始图像被丢弃，以减少内存消耗。具体来说，我们为第$i$个关键帧保存的状态是
　　　　　　　　　　　　　　　
其中，$i$是帧的索引，${\hat{p}}_i^w$和${\hat{q}}_i^w$分别是来自VIO的位置和旋转。如果这个帧有一个回环帧，$v$是回环帧的索引。${\hat{p}}_{iv}^w$和${\hat{\psi }}_{iv}$是通过重定位得到的两帧之间的相对位置和偏航角。$D(u,v,des)$是特征集。每个特征都包含二维位置及其BRIEF描述子。

F.位姿图加载

  我们使用相同的保存格式来加载关键帧。每个关键帧都是位姿图中的一个顶点。顶点的初始姿态为${\hat{p}}_i^w$和${\hat{q}}_i^w$。回环边由回环信息${\hat{p}}_{iv}^w$和${\hat{\psi }}_{iv}$直接建立。每个关键帧与它的邻居关键帧建立几个顺序边，如公式(19)。加载位姿图后，我们立即执行一次全局4自由度位姿图。位姿图的保存和加载速度与位姿图的大小呈线性相关。

9．实验结果

  我们执行数据集、现实世界的实验以及两个应用程序来评估提出的VINS-Mono系统。在第一个实验中，我们将提出的算法与另一个最先进的算法在公共数据集上进行了比较。我们进行了数值分析，以显示我们的系统在细节上的准确性。然后，我们在室内环境中测试我们的系统，以评估在重复场景中的性能。通过一个大场景实验验证了该方法的长期实用性。此外，我们将所提出的系统应用于两个应用程序。在航空机器人应用中，我们使用VINS-Mono作为位置反馈来控制无人机追踪预定的轨迹。然后我们将我们的方法移植到iOS移动设备上。
　　后面翻译略