01背包问题

题目描述：

有n个物品，每个物品有两个属性：一个是体积$w_i$,一个是价值$v_1$，可以表示为：$(w_1,v_1),(w_1,v_1),\dots ,(w_1,v_n)$。同时我们还有一背包，背包的容量用W表示。现在我们将物品放入背包，放入的物品体积的总和不得超过背包的体积。
问:这个背包能装下的最大价值。

深度优先搜索：

代码：

#include 
#include 
using namespace std;
#define Max_n 105
#define Max_W 10000

int n,W;
int w[Max_n],v[Max_n];
//goods_index:当前搜索到的物品下标
//residue_W:背包剩余容量
int DFS(int goods_index,int residue_W)
{
    if(goods_index==n){
        //已经没有物品
        return 0;
    }
    if(residue_W<w[goods_index]){
        //当前物品已经放不进去
        return DFS(goods_index+1,residue_W);
    }
    if(residue_W>=w[goods_index]){
        //当前物品可以放进去,有两种选择放或不放
        return max(v[goods_index]+DFS(goods_index+1,residue_W-w[goods_index]),DFS(goods_index+1,residue_W));
    }
}

说明：

• 算法每一步都有两个选择所以时间复杂度为：$O(2^n)$。
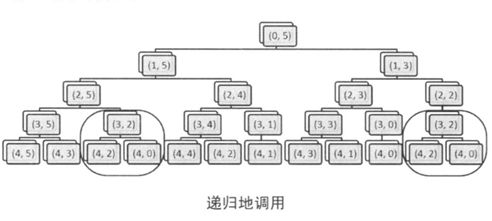
• DFS的搜索树如下，每一层代表一个物品的搜索，中间的数字对表示递归DFS的参数，我们可以发现：我们用参数(3,2)重复调用了DFS两次，我们知道一个函数只要我们传进去的参数一样返回的结果一定是一样的，所以这两次是重复计算。我们称这个现象为重叠子问题
  

记录状态的动态规划：

• 为了解决上面的重叠子问题，我们使用剪枝来优化，我们定义一个二维数组$DP[i][j]$来记录用参数$(i,j)$调用DFS后返回的结果，这样第二次再要用$(i,j)$参数调用DFS时我们可以直接返回DP中保存的结果以实现剪枝。这个算法叫做记录状态的动态规划。这样DFS调用的次数是他的参数$(i,j)$的所以可能性的个数，$1\le i\le n，1\le j\le W$，所以最终算法的时间复杂度为$O(n\ast W)$,代码如下：

#include 
#include 
using namespace std;
#define Max_n 105
#define Max_W 10000

int n,W;
int w[Max_n],v[Max_n];
//全局变量默认为0
int DP[Max_n][Max_W]; //记录状态的数组
memset(DP,-1,sizeof(DP));

//goods_index:当前搜索到的物品下标
//residue_W:背包剩余容量
int DFS(int goods_index,int residue_W)
{
    if (DP[goods_index][residue_W]>=0){
        return DP[goods_index][residue_W];
    }
    if(goods_index==n){
        //已经没有物品
        return DP[goods_index][residue_W]=0;
    }
    if(residue_W<w[goods_index]){
        //当前物品已经放不进去
        return DP[goods_index][residue_W]=DFS(goods_index+1,residue_W);
    }
    if(residue_W>=w[goods_index]){
        //当前物品可以放进去,有两种选择放或不放
        return DP[goods_index][residue_W]=max(v[goods_index]+DFS(goods_index+1,residue_W-w[goods_index]),
                                              DFS(goods_index+1,residue_W));
    }
}

说明：

• memset(DP,-1,sizeof(DP))：该函数按照字节对内存进行填充，可以用来初始化全0或全-1的数组，应该全0的每一个二进制为都是0，-1的每个二进制为都是1.

递推形式的动态规划：

• 我们先分析一下上面DP数组的含义，$DP[i][j]$：记录的是$DFS(i,j)$的返回结果，即：我们用容量为$j$的背包去装编号从$i$到$n-1$(下标从0开始)这几个物品得到的最大价值。根据这个含义我们可以知道我们的结果最后是存在$DP[0][W]$中。
• 现在假设DP矩阵的$(i-1)到n$行我们都已经得到，现在我们求DP数组的第$i$行，使用下面公式:
  $$dp[i][j]=\{\begin{array}{ll}dp[i+1][j]& (j<w[i])\\ max(dp[i+1][j],dp[i+1][j-w[i]]+v[i])& 其他\end{array}$$
• 有上面的递推公式我们可以得出整个DP数组。最后输出$DP[0][W]$

代码：

#include 
#include 
using namespace std;
#define Max_n 105
#define Max_W 10000

int n,W;
int w[Max_n],v[Max_n];
//全局变量默认为0
int DP[Max_n][Max_W]; //记录状态的数组

void Dynamic_degradation(){
    for(int i=n-1;i>=0;i--){
        for(int j=0;j<=W;j++){
            if(j<w[i])
                DP[i][j]=DP[i+1][j];
            else
                DP[i][j]=max(DP[i+1][j],DP[i+1][j-w[i]]+v[i]);
        }
    }
    cout<<DP[0][W]<<endl;
}