数据结构与算法 知识点总结(中)---线性表,堆栈,队列
Table of Contents
数据结构概念
常见数据结构
. 数组
数组下标运算法:
数组程序设计
. 线性表
链表Linked List
单向链表:
双向链表:
循环链表
单向、双向、循环链表区别:
链表的应用:
C代码:
接口声明
接口实现
. 堆栈
2.1 操作
2.2 特点
2.3 抽象定义
2.4 软件堆栈
2.4.1 数组堆栈
2.4.2 串列堆栈
架构层次上的堆栈通常被用以申请和访问内存。
2.4.3 堆栈应用举例
. 队列
3.1 单链队列
3.2 循环队列
3.3 阵列队列
![]()
![]()
数据结构概念
在计算机科学中,数据结构(data structure)是计算机中存储、组织数据的方式。
数据结构意味着接口或封装:一个数据结构可被视为两个函数之间的接口,或者是由数据类型联合组成的存储内容的访问方法封装。
大多数数据结构都由数列、记录、可辨识联合、引用等基本类型构成。举例而言,可为空的引用(nullable reference)是引用与可辨识联合的结合体,而最简单的链式结构链表则是由记录与可空引用构成。
数据结构可透过编程语言所提供的数据类型、引用及其他操作加以实现。一个设计良好的数据结构,应该在尽可能使用较少的时间与空间资源的前提下,支持各种程序运行。
不同种类的数据结构适合不同种类的应用,部分数据结构甚至是为了解决特定问题而设计出来的。例如B树即为加快树状结构访问速度而设计的数据结构,常被应用在数据库和文件系统上。
正确的数据结构选择可以提高算法的效率(请参考算法效率)。在计算机程序设计的过程中,选择适当的数据结构是一项重要工作。许多大型系统的编写经验显示,程序设计的困难程度与最终成果的质量与表现,取决于是否选择了最适合的数据结构。
系统架构的关键因素是数据结构而非算法的见解,导致了多种形式化的设计方法与编程语言的出现。绝大多数的语言都带有某种程度上的模块化思想,透过将数据结构的具体实现封装隐藏于用户界面之后的方法,来让不同的应用程序能够安全地重用这些数据结构。C++、Java、Python等面向对象的编程语言可使用类 (计算机科学)来达到这个目的。
因为数据结构概念的普及,现代编程语言及其API中都包含了多种默认的数据结构,例如 C++ 标准模板库中的容器、Java集合框架以及微软的.NET Framework。
常见数据结构
- 数组(Array)
- 堆栈(Stacks)
- 队列(Queues)
- 链表(Linked List)
- 树(Tree)
- 图(Graphs)
- 堆积(Heap)
- 散列表(Hash)
1. 数组
在计算机科学中,数组数据结构(英语:array data structure),简称数组(英语:Array),是由相同类型的元素(element)的集合所组成的数据结构,分配一块连续的内存来存储。利用元素的索引(index)可以计算出该元素对应的存储地址。
最简单的数据结构类型是一维数组。例如,索引为0到9的32位整数数组,可作为在存储器地址2000,2004,2008,...2036中,存储10个变量,因此索引为i的元素即在存储器中的2000+4×i地址。数组第一个元素的存储器地址称为第一地址或基础地址。
二维数组,对应于数学上的矩阵概念,可表示为二维矩形格。例如:
在C中表示为int a[3][3] = {{3, 6, 2}, {0, 1,-4}, {2, -1, 0}};
数组一词通常用于表示数组数据类型,一种大多数高端编程语言都会内置的数据类型。数组类型通常由数组结构来实现;然而在某些语言中,它们可以由散列表、链表、搜索树或其它数据结构来实现。
在算法的描述中,数组一词特别着重意义为关系数组或“抽象的数组”,一种理论上的计算机科学模型(抽象数据类型或 ADT),专注于数组的基本性质上。
【历史】
第一台数字计算机使用机器语言编程来设置和访问数据表,向量和矩阵计算的数组结构,以及许多其它目的。1945年,在创建第一个范纽曼型架构计算机时,约翰·冯·诺伊曼(John von Neumann)写了第一个数组排序程序(合并排序)。数组索引最初是通过自修改代码,后来使用索引寄存器和间接定址来完成的。1960年代设计的一些主机,如Burroughs B5000及其后继者,使用存储器分段来运行硬件中的索引边界检查。
数组名作为数组实体的标识符,具有特殊性,不同于整型、浮点型、指针型或结构类型等变量标识符。这是因为数组是一组元素的聚集,不能把一个聚集看作一个值直接读出(这个值指的是右值),也不能把一个聚集看作一个地址直接赋值(即左值)。因此,数组名作为左值、右值,在C语言标准中都有特殊规定:
- 作为
sizeof的操作数,数组名代表数组对象本身; - 作为取地址运算符
&的操作数,数组名代表数组对象本身[注 3]; - 作为字符串字面量用于初始化一个数组;
- 其他情形,表达式中的数组名从数组类型被自动转化为指向数组首元素的指针类型表达式(右值)。[注 4]
例如,
1 char s[] = "hello";
2
3 int main() {
4 char (*p1)[6] = &s; // OK!
5 char (*p2)[6] = s; // compile error: cannot convert 'char*' to 'char (*)[6]'
6 char *p3 = &s; // compile error: cannot convert 'char (*)[6]' to 'char*' in initialization
7 }根据上述C语言标准中的规定,表达式&s的值的类型是char (*)[6],即指向整个数组的指针;而表达式 s 则被隐式转换为指向数组首元素的指针值,即 char* 类型。同理,表达式s[4],等效于表达式*(s+4)。
数组下标运算法:
C语言标准中定义,数组下标运算(array subscripting)有两个运算数,一个为到类型type的指针表达式,另一个运算符为整数表达式,结果为类型type。但没有规定两个运算数的先后次序。因此,有以下推论:
- 两个运算数可以交换顺序,即 p[N] 与 N[p] 是等价的,为 *(p+N) ;
- 数组下标运算,既可以适用于数组名(实际上隐式把数组名转换为指向数组首元素的指针表达式),也可以适用于指针表达式;
- 整型表达式可以取负值。
例如:
1 int a[10], *p = a;
2 p[0] = 10;
3 (p + 1)[0] = 20;
4 0[p + 1] = 10;数组程序设计
数组设计之初是在形式上依赖内存分配而成的,所以必须在使用前预先请求空间。这使得数组有以下特性:
- 请求空间以后大小固定,不能再改变(数据溢出问题);
- 在内存中有空间连续性的表现,中间不会存在其他程序需要调用的数据,为此数组的专用内存空间;
- 在旧式编程语言中(如有中阶语言之称的C),程序不会对数组的操作做下界判断,也就有潜在的越界操作的风险(比如会把数据写在运行中程序需要调用的核心部分的内存上)。
因为简单数组强烈倚赖计算机硬件之内存,所以不适用于现代的程序设计。欲使用可变大小、硬件无关性的数据类型,Java等程序设计语言均提供了更高级的数据结构:ArrayList、Vector等动态数组。
2. 线性表
链表Linked List
链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而顺序表相应的时间复杂度分别是O(logn)和O(1)。
优缺点:
- 使用链表结构可以克服数组链表需要预先知道数据大小的缺点,
- 链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。
- 但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。
在计算机科学中,链表作为一种基础的数据结构可以用来生成其它类型的数据结构。链表通常由一连串节点组成,每个节点包含任意的实例数据(data fields)和一或两个用来指向上一个/或下一个节点的位置的链接("links")。链表最明显的好处就是,常规数组排列关联项目的方式可能不同于这些数据项目在记忆体或磁盘上顺序,数据的访问往往要在不同的排列顺序中转换。而链表是一种自我指示数据类型,因为它包含指向另一个相同类型的数据的指针(链接)。链表允许插入和移除表上任意位置上的节点,但是不允许随机存取。
链表有很多种不同的类型:单向链表,双向链表以及循环链表。
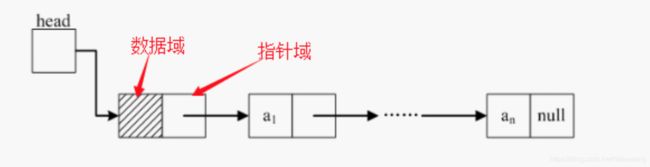
单向链表:
链表中最简单的一种是单向链表,它包含两个域,一个信息域和一个指针域。这个链接指向列表中的下一个节点,而最后一个节点则指向一个空值。
基本思想:元素的存储空间是离散的,单独的(物理),它们可以通过在逻辑上指针的联系使得它成为了整体的链表。存储结构如下图:
一个单向链表包含两个值: 当前节点的值和一个指向下一个节点的链接
一个单向链表的节点被分成两个部分。第一个部分保存或者显示关于节点的信息,第二个部分存储下一个节点的地址。单向链表只可向一个方向遍历。
【域】 链表最基本的结构是在每个节点保存数据和到下一个节点的地址,在最后一个节点保存一个特殊的结束标记,另外在一个固定的位置保存指向第一个节点的指针,有的时候也会同时储存指向最后一个节点的指针。
【查找方式】一般查找一个节点的时候需要从第一个节点开始每次访问下一个节点,一直访问到需要的位置。但是也可以提前把一个节点的位置另外保存起来,然后直接访问。当然如果只是访问数据就没必要了,不如在链表上储存指向实际数据的指针。这样一般是为了访问链表中的下一个或者前一个(需要储存反向的指针,见下面的双向链表)节点。
相对于下面的双向链表,这种普通的,每个节点只有一个指针的链表也叫单向链表,或者单链表,通常用在每次都只会按顺序遍历这个链表的时候(例如图的邻接表,通常都是按固定顺序访问的)。
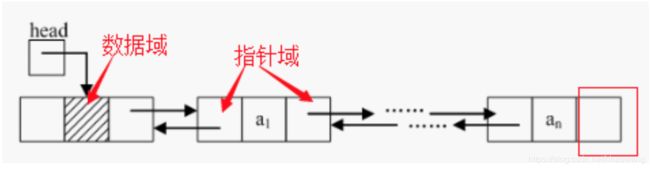
双向链表:
一种更复杂的链表是“双向链表”或“双面链表”。每个节点有两个连接:一个指向前一个节点,(当此“连接”为第一个“连接”时,指向空值或者空列表);而另一个指向下一个节点,(当此“连接”为最后一个“连接”时,指向空值或者空列表)
一个双向链表有三个整数值:
- 数值;
- 向后的节点链接;
- 向前的节点链接。
【双向链表特点:】
双向链表中不仅有指向后一个节点的指针,还有指向前一个节点的指针。这样可以从任何一个节点访问前一个节点,当然也可以访问后一个节点,以至整个链表。
用途:一般是在需要大批量的另外储存数据在链表中的位置的时候用。双向链表也可以配合下面的其他链表的扩展使用。
由于另外储存了指向链表内容的指针,并且可能会修改相邻的节点,有的时候第一个节点可能会被删除或者在之前添加一个新的节点。这时候就要修改指向首个节点的指针。有一种方便的可以消除这种特殊情况的方法是在最后一个节点之后、第一个节点之前储存一个永远不会被删除或者移动的虚拟节点,形成一个下面说的循环链表。这个虚拟节点之后的节点就是真正的第一个节点。这种情况通常可以用这个虚拟节点直接表示这个链表,对于把链表单独的存在数组里的情况,也可以直接用这个数组表示链表并用第0个或者第-1个(如果编译器支持)节点固定的表示这个虚拟节点。
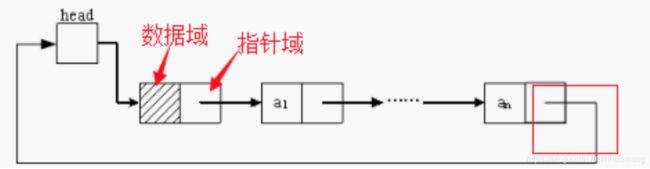
循环链表
在一个 循环链表中, 首节点和末节点被连接在一起。这种方式在单向和双向链表中皆可实现。要转换一个循环链表,你开始于任意一个节点然后沿着列表的任一方向直到返回开始的节点。再来看另一种方法,循环链表可以被视为“无头无尾”。这种列表很利于节约数据存储缓存, 假定你在一个列表中有一个对象并且希望所有其他对象迭代在一个非特殊的排列下。
指向整个列表的指针可以被称作访问指针。
用单向链表构建的循环链表
循环链表中第一个节点之前就是最后一个节点,反之亦然。循环链表的无边界使得在这样的链表上设计算法会比普通链表更加容易。对于新加入的节点应该是在第一个节点之前还是最后一个节点之后可以根据实际要求灵活处理,区别不大(详见下面实例代码)。当然,如果只会在最后插入数据(或者只会在之前),处理也是很容易的。
另外有一种模拟的循环链表,就是在访问到最后一个节点之后的时候,手工的跳转到第一个节点。访问到第一个节点之前的时候也一样。这样也可以实现循环链表的功能,在直接用循环链表比较麻烦或者可能会出现问题的时候可以用。
单向、双向、循环链表区别:
1、它们都有数据域(data(p))和指针域(next(p)),但是从图中可以看出双链表有两个指针域,一个指向它的前节点,一个指向它的后节点。
2、单链表最后一个节点的指针域为空,没有后继节点;循环链表和双链表最后一个节点的指针域指向头节点,下一个结点为头节点,构成循环;
3、单链表和循环链表只可向一个方向遍历;双链表和循环链表,首节点和尾节点被连接在一起,可视为“无头无尾”;双链表可以向两个方向移动,灵活度更大。
链表的应用:
链表用来构建许多其它数据结构,如堆栈,队列和他们的派生。
节点的数据域也可以成为另一个链表。通过这种手段,我们可以用列表来构建许多链性数据结构;这个实例产生于Lisp编程语言,在Lisp中链表是初级数据结构,并且现在成为了常见的基础编程模式。 有时候,链表用来生成联合数组,在这种情况下我们称之为联合数列。这种情况下用链表会优于其它数据结构,如自平对分查找树(self-balancing binary search trees)甚至是一些小的数据集合。不管怎样,一些时候一个链表在这样一个树中创建一个节点子集,并且以此来更有效率地转换这个集合。
C代码:
范例代码是一个ADT(抽象数据类型)双向环形链表的基本操作部分的实例(未包含线程安全机制),全部遵从ANSI C标准。
接口声明
#ifndef LLIST_H
#define LLIST_H
/* linear list */
typedef void node_proc_fun_t(void*);
typedef int node_comp_fun_t(const void*, const void*);
typedef void LLIST_T;
LLIST_T *llist_new(int elmsize);
int llist_delete(LLIST_T *ptr);
int llist_node_append(LLIST_T *ptr, const void *datap);
int llist_node_prepend(LLIST_T *ptr, const void *datap);
int llist_travel(LLIST_T *ptr, node_proc_fun_t *proc);
void llist_node_delete(LLIST_T *ptr, node_comp_fun_t *comp, const void *key);
void *llist_node_find(LLIST_T *ptr, node_comp_fun_t *comp, const void *key);
#endif接口实现
类型定义
1 struct node_st {
2 void *datap;
3 struct node_st *next, *prev;
4 };
5
6 struct llit_st {
7 struct node_st head;
8 int lmsize;
9 int elmnr;
10 };初始化和销毁
1 LLIST_T *
2 llist_new(int elmsize) {
3 struct llist_st *newlist;
4 newlist = malloc(sizeof(struct llist_st));
5 if (newlist == NULL)
6 return NULL;
7 newlist->head.datap = NULL;
8 newlist->head.next = &newlist->head;
9 newlist->head.prev = &newlist->head;
10 newlist->elmsize = elmsize;
11 return (void *)newlist;
12 }
13
14 int llist_delete(LLIST_T *ptr) {
15 struct llist_st *me = ptr;
16 struct node_st *curr, *save;
17 for (curr = me->head.next ;
18 curr != &me->head ; curr = save) {
19 save = curr->next;
20 free(curr->datap);
21 free(curr);
22 }
23 free(me);
24 return 0;
25 }节点插入
1 int llist_node_append(LLIST_T *ptr, const void *datap) {
2 struct llist_st *me = ptr;
3 struct node_st *newnodep;
4 newnodep = malloc(sizeof(struct node_st));
5 if (newnodep == NULL)
6 return -1;
7 newnodep->datap = malloc(me->elmsize);
8 if (newnodep->datap == NULL) {
9 free(newnodep);
10 return -1;
11 }
12 memcpy(newnodep->datap, datap, me->elmsize);
13 me->head.prev->next = newnodep;
14 newnodep->prev = me->head.prev;
15 me->head.prev = newnodep;
16 newnodep->next = &me->head;
17 return 0;
18 }
19
20 int llist_node_prepend(LLIST_T *ptr, const void *datap) {
21 struct llist_st *me = ptr;
22 struct node_st *newnodep;
23 newnodep = malloc(sizeof(struct node_st));
24 if (newnodep == NULL)
25 return -1;
26 newnodep->datap = malloc(me->elmsize);
27 if (newnodep->datap == NULL) {
28 free(newnodep);
29 return -1;
30 }
31 memcpy(newnodep->datap, datap, me->elmsize);
32 me->head.next->prev = newnodep;
33 newnodep->next = me->head.next;
34 me->head.next = newnodep;
35 newnodep->prev = &me->head;
36 return 0;
37 }
遍历
1 int llist_travel(LLIST_T *ptr, node_proc_fun_t *proc) {
2 struct llist_st *me = ptr;
3 struct node_st *curr;
4 for (curr = me->head.next;
5 curr != &me->head ; curr = curr->next)
6 proc(curr->datap); // proc(something you like)
7 return 0;
8 }
删除和查找
1 void llist_node_delete(LLIST_T *ptr,
2 node_comp_fun_t *comp,
3 const void *key) {
4 struct llist_st *me = ptr;
5 struct node_st *curr;
6 for (curr = me->head.next;
7 curr != &me->head; curr = curr->next) {
8 if ( (*comp)(curr->datap, key) == 0 ) {
9 struct node_st *_next, *_prev;
10 _prev = curr->prev; _next = curr->next;
11 _prev->next = _next; _next->prev = _prev;
12 free(curr->datap);
13 free(curr);
14 break;
15 }
16 }
17 return;
18 }
19
20 void *llist_node_find(LLIST_T *ptr,
21 node_comp_fun_t *comp, const void *key) {
22 struct llist_st *me = ptr;
23 struct node_st *curr;
24 for (curr = me->head.next;
25 curr != &me->head; curr = curr->next) {
26 if ( (*comp)(curr->datap, key) == 0 )
27 return curr->datap;
28 }
29 return NULL;
30 }常用于组织删除、检索较少,而添加、遍历较多的数据。 如果与上述情形相反,应采用其他数据结构或者与其他数据结构组合使用。
2. 堆栈Stack
堆栈(英语:stack)又称为栈或堆叠,是计算机科学中的一种抽象数据类型,只允许在有序的线性数据集合的一端(称为堆栈顶端,英语:top)进行加入数据(英语:push)和移除数据(英语:pop)的运算。因而按照后进先出(LIFO, Last In First Out)的原理运作。
堆栈常与另一种有序的线性数据集合队列相提并论。
2.1 操作
堆栈使用两种基本操作:推入(压栈,push)和弹出(出栈,pop):
- 推入(压栈操作):将数据放入堆栈顶端,堆栈顶端移到新放入的数据。
- 弹出(出栈操作):将堆栈顶端数据移除,堆栈顶端移到移除后的下一笔数据。
2.2 特点
堆栈的基本特点:
- 先入后出,后入先出。
- 除头尾节点之外,每个元素有一个前驱,一个后继。
2.3 抽象定义
函数签名:
init: -> Stack
push: N x Stack -> Stack
top: Stack -> (N U ERROR)
pop: Stack -> Stack
isempty: Stack -> Boolean此处的N代表某个元素(如自然数),而U表示集合求交。
语义:
top(init()) = ERROR
top(push(i,s)) = i
pop(init()) = init()
pop(push(i, s)) = s
isempty(init()) = true
isempty(push(i, s)) = false
2.4 软件堆栈
堆栈可以用数组和链表两种方式实现,一般为一个堆栈预先分配一个大小固定且较合适的空间并非难事,所以较流行的做法是Stack结构下含一个数组。如果空间实在紧张,也可用链表实现,且去掉表头。
这里的例程是以C语言实现的。
2.4.1 数组堆栈
#include
#include
#include
#define stack struct Stack
#define STACK_POP_ERR 42
// 堆疊資料結構 堆栈数据结构
struct Stack {
int val[10]; // 陣列空間
int top; // 堆疊頂端指標(栈顶)
};
// 檢查堆疊是否為空
bool empty(stack *stk) {
return stk->top == 0;
}
// 推入資料
void push(stack *stk, int x) {
stk->top = stk->top + 1;
stk->val[stk->top] = x;
}
// 彈出并返回資料
int pop(stack *stk) {
if (empty(stk))
return STACK_POP_ERR; // 不能彈出
else {
stk->top = stk->top - 1;
return stk->val[stk->top + 1];
}
}
int main() {
// 宣告并初始化資料結構空間
stack stk;
stk.top = 0;
// 推入四个
push(&stk, 3);
push(&stk, 4);
push(&stk, 1);
push(&stk, 9);
// 弹出三个
printf("%d ", pop(&stk));
printf("%d ", pop(&stk));
printf("%d ", pop(&stk));
return 0;
} 2.4.2 串列堆栈
#include
#include
#include
#define elemType int /* 链栈元素数据类型,以整型为例 */
#define SNODE_SIZE sizeof (struct sNode) /* 链栈结点空间大小 */
#define status int /* 状态型变量 */
#define OVERFLOW -1 /* 内存溢出状态码 */
#define ERROR 0 /* 错误状态码 */
#define OK 1 /* 正确状态码 */
/* 链栈结点存储结构 */
typedef struct sNode {
elemType data;
struct sNode *next;
} sNode, *sNodePtr;
/* 链栈存储结构 */
typedef struct linkStack {
sNodePtr top; /* 栈顶指针 */
} linkStack;
/* 初始化 */
/* 操作结果:构造一个带头结点的空链栈S */
void initStack (linkStack *S) {
S->top = (sNodePtr) malloc (SNODE_SIZE); /* 产生头结点,栈顶指针指向此头结点 */
if (!S->top) /* 内存分配失败 */
exit (OVERFLOW);
S->top->next = NULL;
}
/* 销毁 */
/* 初始条件:链栈S已存在。操作结果:销毁链栈S */
void destroyStack (linkStack *S) {
sNodePtr p, q;
p = S->top; /* p指向S的头结点 */
while (p) {
q = p->next; /* q指向p的下一个结点 */
free (p); /* 回收p指向的结点 */
p = q; /* p移动到下一个结点 */
} /* 直到没有下一个结点 */
}
/* 清空 */
/* 初始条件:链栈S已存在。操作结果:将S重置为空栈 */
void clearStack (linkStack *S) {
sNodePtr p, q;
p = S->top->next; /* p指向栈的第一个结点 */
while (p) {
q = p->next; /* q指向p的下一个结点 */
free (p); /* 回收p指向的结点 */
p = q; /* p移动到下一个结点 */
} /* 直到没有下一个结点 */
S->top->next = NULL;
}
/* 判断链栈是否为空 */
/* 初始条件:链栈S已存在。操作结果:若S为空链栈,则返回TRUE,否则返回FALSE */
status stackIsEmpty (linkStack *S) {
return S->top->next == NULL;
}
/* 求链栈长度 */
/* 初始条件:链栈S已存在。操作结果:返回S中数据元素个数 */
int stackLength (linkStack *S) {
int i = 0;
sNodePtr p;
p = S->top->next; /* p指向栈的第一个结点 */
while (p) { /* 未到栈尾 */
i++;
p = p->next;
}
return i;
}
/* 获取栈顶元素 */
/* 初始条件:链栈S已存在。操作结果:当栈不为空时,将栈顶元素其值赋给e并返回OK,否则返回ERROR */
status getTopElem (linkStack *S, elemType *e) {
sNodePtr p;
if (stackIsEmpty (S))
return ERROR;
p = S->top->next; /* p指向栈的第一个结点 */
*e = p->data;
return OK;
}
/* 入栈 */
/* 操作结果:在S的栈顶插入新的元素e */
status push (linkStack *S, elemType e) {
sNodePtr p;
p = (sNodePtr) malloc (SNODE_SIZE); /* 产生新结点 */
if (!p) /* 内存分配失败 */
exit (OVERFLOW);
p->data = e;
p->next = S->top->next; /* 将新结点链接到原栈顶 */
S->top->next = p; /* 栈顶指向新结点 */
}
/* 出栈 */
/* 操作结果:删除S的栈顶元素,并由e返回其值 */
status pop (linkStack *S, elemType *e) {
sNodePtr p;
if (stackIsEmpty (S))
return ERROR;
p = S->top->next; /* p指向链栈的第一个结点 */
*e = p->data; /* 取出数据 */
S->top->next = p->next;
free (p); /* 删除该结点 */
if (S->top == p) /* 栈为空 */
S->top->next = NULL;
return OK;
}
/* 打印栈内容 */
/* 初始条件:链栈S已存在。操作结果:当栈不为空时,打印栈内容并返回OK,否则返回ERROR */
status printStack (linkStack *S) {
sNodePtr p;
if (stackIsEmpty (S))
return ERROR;
p = S->top->next;
while (p) {
printf ("%d\t", p->data);
p = p->next;
}
putchar ('\n');
return OK;
} 架构层次上的堆栈通常被用以申请和访问内存。
2.4.3 堆栈应用举例
1、回溯法
回溯法(英语:backtracking)是暴力搜索法中的一种。
对于某些计算问题而言,回溯法是一种可以找出所有(或一部分)解的一般性算法,尤其适用于约束满足问题(在解决约束满足问题时,我们逐步构造更多的候选解,并且在确定某一部分候选解不可能补全成正确解之后放弃继续搜索这个部分候选解本身及其可以拓展出的子候选解,转而测试其他的部分候选解)。
回溯法采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
- 找到一个可能存在的正确的答案
- 在尝试了所有可能的分步方法后宣告该问题没有答案
在最坏的情况下,回溯法会导致一次复杂度为指数时间的计算。
例子:用回溯法解决八皇后问题
#include
#define PRINTF_IN 1 //定义是否打印,1:打印,0:不打印
int queens(int Queens){
int i, k, flag, not_finish=1, count=0;
//正在处理的元素下标,表示前i-1个元素已符合要求,正在处理第i个元素
int a[Queens+1]; //八皇后问题的皇后所在的行列位置,从1幵始算起,所以加1
i=1;
a[1]=1; //为数组的第一个元素赋初值
printf("%d皇后的可能配置是:",Queens);
while(not_finish){ //not_finish=l:处理尚未结束
while(not_finish && i<=Queens){ //处理尚未结束且还没处理到第Queens个元素
for(flag=1,k=1; flag && k1 && a[i]==Queens)
a[i]=1; //当a[i]为Queens时将a[i]的值置1
else
if(i==1 && a[i]==Queens)
not_finish=0; //当第一位的值达到Queens时结束
else
a[i]++; //将a[il的值取下一个值
}else if(a[i] == Queens)
a[i]=1;
else
a[i]++; //将a[i]的值取下一个值
}else if(++i<=Queens)
if(a[i-1] == Queens )
a[i]=1; //若前一个元素的值为Queens则a[i]=l
else
a[i] = a[i-1]+1; //否则元素的值为前一个元素的下一个值
}
if(not_finish){
++count;
if(PRINTF_IN){
printf((count-1)%3 ? " [%2d]:" : "\n[%2d]:", count);
for(k=1; k<=Queens; k++) //输出结果
printf(" %d", a[k]);
}
if(a[Queens-1] 2、 深度优先搜索
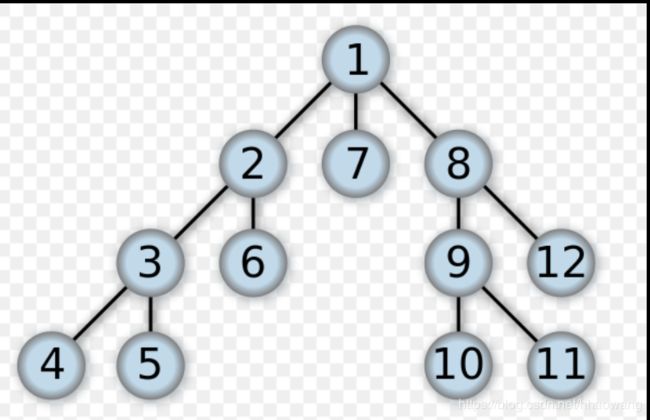
深度优先搜索算法(英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
深度优先搜索是图论中的经典算法,利用深度优先搜索算法可以产生目标图的相应拓扑排序表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。
实现方法
- 首先将根节点放入队列中。
- 从队列中取出第一个节点,并检验它是否为目标。
如果找到目标,则结束搜寻并回传结果。
否则将它某一个尚未检验过的直接子节点加入队列中。
- 重复步骤2。
- 如果不存在未检测过的直接子节点。
将上一级节点加入队列中。
重复步骤2。
- 重复步骤4。
- 若队列为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
3. 队列
队列,又称为伫列(queue),是先进先出(FIFO, First-In-First-Out)的线性表。在具体应用中通常用链表或者数组来实现。队列只允许在后端(称为rear)进行插入操作,在前端(称为front)进行删除操作。
队列的操作方式和堆栈类似,唯一的区别在于队列只允许新数据在后端进行添加。
3.1 单链队列
单链队列使用链表作为基本数据结构,所以不存在伪溢出的问题,队列长度也没有限制。但插入和读取的时间代价较高
1 // 定义单链队列的存储结构
2 typedef struct QNode {
3 int data;
4 QNode *next;
5 }QNode,*QNodePtr;
6
7 typedef struct LinkQueue{
8 //队头 队尾 指针
9 QNodePtr front,rear;
10 }LinkQueue;
11
12
13 // 构造一个空队列Q
14 LinkQueue* Q_Init() {
15 //申请内存
16 LinkQueue* Q = (LinkQueue*)malloc(sizeof(LinkQueue));
17 //如果 Q 为 NULL 说明 内存申请失败,结束程序
18 if (!Q)
19 exit(OVERFLOW);
20 //初始化头尾节点 指向相同地址
21 Q->front = Q->rear = (QNodePtr)malloc(sizeof(QNode));
22 //如果 Q->front 为 NULL 说明 内存申请失败,结束程序
23 if (!Q->front)
24 exit(OVERFLOW);
25 Q->front->next = NULL;
26 return Q;
27 }
28
29 // 销毁队列Q(无论空否均可)
30 void Q_Destroy(LinkQueue *Q) {
31 while (Q->front) {
32 //将队尾指向队头下一个节点的地址(第1个节点)
33 Q->rear = Q->front->next;
34 //回收队头
35 free(Q->front);
36 //将队头指向队尾(相当于第1个节点变成了队头,然后依次第2个第3个、、、
37 //直到没有下一个节点,也就是 Q->front == NULL 的时候)
38 Q->front = Q->rear;
39 }
40 free(Q);
41 }
42
43 // 将Q清为空队列
44 void Q_Clear(LinkQueue *Q) {
45 QNodePtr p, q;
46 //将队尾指向队头点的地址
47 Q->rear = Q->front;
48 //取出第1个节点
49 p = Q->front->next;
50 //回收第1个节点
51 Q->front->next = NULL;
52 while (p) {
53 //将 q 指向 p(第1个节点)
54 q = p;
55 //将 p 指向 第2个节点
56 p = p->next;
57 //回收第2个节点
58 free(q);
59 }
60 }
61
62 // 若Q为空队列,则返回-1,否则返回1
63 int Q_Empty(LinkQueue Q) {
64 if (Q.front->next == NULL)
65 return 1;
66 else
67 return -1;
68 }
69
70 // 求队列的长度
71 int Q_Length(LinkQueue Q) {
72 int i = 0;
73 QNodePtr p;
74 p = Q.front;
75 //遍历队列中的节点,直到队尾等于队头
76 while (Q.rear != p) {
77 i++;
78 p = p->next;
79 }
80 return i;
81 }
82
83 // 打印队列中的内容
84 void Q_Print(LinkQueue Q) {
85 int i = 0;
86 QNodePtr p;
87 p = Q.front;
88 while (Q.rear != p) {
89 i++;
90 cout << p->next->data << endl;
91 p = p->next;
92 }
93 }
94
95 // 若队列不空,则用e返回Q的队头元素,并返回1,否则返回-1
96 int Q_GetHead(LinkQueue Q, int &e) {
97 QNodePtr p;
98 if (Q.front == Q.rear)
99 return -1;
100 p = Q.front->next;
101 e = p->data;
102 return 1;
103 }
104
105 // 插入元素e为Q的新的队尾元素
106 void Q_Put(LinkQueue *Q, int e) {
107 QNodePtr p = (QNodePtr)malloc(sizeof(QNode));
108 if (!p) // 存储分配失败
109 exit(OVERFLOW);
110 p->data = e;
111 p->next = NULL;
112 //FIFO,将新节点追加到尾节点后面
113 Q->rear->next = p;
114 //将新的节点变成尾节点
115 Q->rear = p;
116 }
117
118
119 // 若队列不空,删除Q的队头元素,用e返回其值,并返回1,否则返回-1
120 int Q_Poll(LinkQueue *Q,int &e) {
121 QNodePtr p;
122 if (Q->front == Q->rear)
123 return -1;
124 //取出头节点
125 p = Q->front->next;
126 //取出头节点的数据
127 e = p->data;
128 cout << e << endl;
129 Q->front->next = p->next;
130 if (Q->rear == p)
131 Q->rear = Q->front;
132 free(p);
133 cout << e << endl;
134 return 1;
135 }3.2 循环队列
循环队列可以更简单防止伪溢出的发生,但队列大小是固定的。
1 // 队列的顺序存储结构(循环队列)
2 #define MAX_QSIZE 5 // 最大队列长度+1
3 typedef struct {
4 int *base; // 初始化的动态分配存储空间
5 int front; // 头指针,若队列不空,指向队列头元素
6 int rear; // 尾指针,若队列不空,指向队列尾元素的下一个位置
7 } SqQueue;
8
9
10 // 构造一个空队列Q
11 SqQueue* Q_Init() {
12 SqQueue *Q = (SqQueue*)malloc(sizeof(SqQueue));
13 // 存储分配失败
14 if (!Q){
15 exit(OVERFLOW);
16 }
17 Q->base = (int *)malloc(MAX_QSIZE * sizeof(int));
18 // 存储分配失败
19 if (!Q->base){
20 exit(OVERFLOW);
21 }
22 Q->front = Q->rear = 0;
23 return Q;
24 }
25
26 // 销毁队列Q,Q不再存在
27 void Q_Destroy(SqQueue *Q) {
28 if (Q->base)
29 free(Q->base);
30 Q->base = NULL;
31 Q->front = Q->rear = 0;
32 free(Q);
33 }
34
35 // 将Q清为空队列
36 void Q_Clear(SqQueue *Q) {
37 Q->front = Q->rear = 0;
38 }
39
40 // 若队列Q为空队列,则返回1;否则返回-1
41 int Q_Empty(SqQueue Q) {
42 if (Q.front == Q.rear) // 队列空的标志
43 return 1;
44 else
45 return -1;
46 }
47
48 // 返回Q的元素个数,即队列的长度
49 int Q_Length(SqQueue Q) {
50 return (Q.rear - Q.front + MAX_QSIZE) % MAX_QSIZE;
51 }
52
53 // 若队列不空,则用e返回Q的队头元素,并返回OK;否则返回ERROR
54 int Q_GetHead(SqQueue Q, int &e) {
55 if (Q.front == Q.rear) // 队列空
56 return -1;
57 e = Q.base[Q.front];
58 return 1;
59 }
60
61 // 打印队列中的内容
62 void Q_Print(SqQueue Q) {
63 int p = Q.front;
64 while (Q.rear != p) {
65 cout << Q.base[p] << endl;
66 p = (p + 1) % MAX_QSIZE;
67 }
68 }
69
70 // 插入元素e为Q的新的队尾元素
71 int Q_Put(SqQueue *Q, int e) {
72 if ((Q->rear + 1) % MAX_QSIZE == Q->front) // 队列满
73 return -1;
74 Q->base[Q->rear] = e;
75 Q->rear = (Q->rear + 1) % MAX_QSIZE;
76 return 1;
77 }
78
79 // 若队列不空,则删除Q的队头元素,用e返回其值,并返回1;否则返回-1
80 int Q_Poll(SqQueue *Q, int &e) {
81 if (Q->front == Q->rear) // 队列空
82 return -1;
83 e = Q->base[Q->front];
84 Q->front = (Q->front + 1) % MAX_QSIZE;
85 return 1;
86 }3.3 阵列队列
1 #define MAX_QSIZE 10 // 最大队列长度+1
2 // 阵列队列的存储结构
3 struct Queue {
4 int Array[MAX_QSIZE]; // 阵列空间大小
5 int front; // 队头
6 int rear; // 队尾
7 int length; // 队列长度
8 };
9
10 // 构造一个空队列Q
11 Queue* Q_Init() {
12 Queue *Q = (Queue*)malloc(sizeof(Queue));
13 if (!Q){
14 // 存储分配失败
15 exit(OVERFLOW);
16 }
17 //初始化
18 Q->front = Q->rear = Q->length = 0;
19 return Q;
20 }
21
22 // 将Q清为空队列
23 void Q_Clear(Queue *Q) {
24 //清除头尾下标和长度
25 Q->front = Q->rear = Q->length = 0;
26 }
27
28 // 入列
29 int Q_Put(Queue *Q, int x) {
30 //如果当前元素数量等于最大数量 返回 -1
31 if (Q->rear + 1 == MAX_QSIZE) {
32 return -1;
33 }
34 Q->Array[Q->rear] = x;
35 Q->rear = Q->rear + 1;
36 //length + 1
37 Q->length = Q->length + 1;
38 return 1;
39 }
40
41 // 出列
42 int Q_Poll(Queue *Q) {
43 //如果当前元素数量等于最大数量 返回 -1
44 if (Q->front + 1 == MAX_QSIZE)
45 return -1;
46 int x = Q->Array[Q->front];
47 Q->front = Q->front + 1;
48 // 移出后減少1
49 Q->length = Q->length - 1;
50 return x;
51 }
参考博客:
1、 https://blog.csdn.net/qq_34840129/article/details/80781829
主要内容:常见数据结构及其基本操作。
2、 https://blog.csdn.net/he90227/article/details/39183787
主要内容:图形化介绍常见数据结构和算法理想、原理。
数据结构与算法课程的知识架构,仅供学习参考