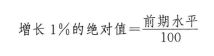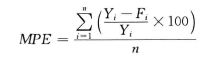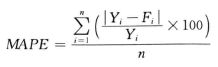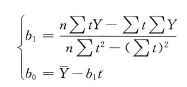《统计学》学习笔记之时间序列分析和预测
鄙人学习笔记
文章目录
- 时间序列分析和预测
- 时间序列及其分解
- 时间序列的描述性分析
- 时间序列预测的程序
- 确定时间序列成分
- 选择预测方法
- 预测方法的评估
- 平稳序列的预测
- 简单平均法
- 移动平均法
- 指数平滑法
- 趋势型序列的预测
- 线性趋势预测
- 非线性趋势预测
- 复合型序列的分解预测
- 确定并分离季节成分
- 建立预测模型并进行预测
- 计算出最后的预测值
时间序列分析和预测
时间序列及其分解
时间序列是同一现象在不同时间上的相继观察值排列而成的序列。
- 平稳及非平稳
时间序列可以分为平稳序列和非平稳序列两大类。
平稳序列是基本上不存在趋势的序列。这类序列中的各观察值基本上在某个固定的水平上波动,虽然在不同的时间段波动的程度不同,但并不存在某种规律,其波动可以看成是随机的。
非平稳序列是包含趋势、季节性或周期性的序列,它可能只含有其中一种成分,也可能是几种成分的组合。
趋势是时间序列在长时期内呈现出来的某种持续上升或持续下降的变动,也称长期趋势。时间序列中的趋势可以是线性的,也可以是非线性的。
季节性也称季节变动,它是时间序列在一年内重复出现的周期性波动。
当然,季节性中的“季节”一词是广义的,它不仅仅是指一年中的四季,其实是指任何一种周期性的变化。
周期性也称循环波动。是时间序列中呈现出来的围绕长期趋势的一种波浪形或振荡式变动。
它不同于趋势变动,不是朝着单一方向的持续运动,而是涨落相间的交替波动。
它也不同于季节变动,季节变动有比较固定的规律,且变动周期大多为一年,循环波动则无固定规律,变动周期多在一年以上,且周期长短不一。
时间序列中除去趋势、周期性和季节性之后的偶然性波动,称为随机性,也称不规则波动。
- 乘法模型和加法模型
时间序列的成分可以分为4种,即趋势T、季节性或季节变动S、周期性或循环波动C、随机性或不规则波动I
传统时间序列分析的一项主要内容就是把这些成分从时间序列中分离出来,并将它们之间的关系用一定的数学关系式予以表达,而后分别进行分析。按4种成分对一时间序列的影响方式不同,时间序列可分解为多种模型,如加法模型、乘法模型。
加法模型:
Y i = T i + S i + C i + I i Y_i=T_i + S_i + C_i + I_i Yi=Ti+Si+Ci+Ii
乘法模型:
Y i = T i ∗ S i ∗ C i ∗ I i Y_i=T_i * S_i * C_i * I_i Yi=Ti∗Si∗Ci∗Ii
时间序列的描述性分析
- 增长率
增长率也称增长速度,它是时间序列中报告期观察值与基期观察值之比减1后的结果,用%表示。由于对比的基期不同,增长率可以分为环比增长率和定基增长率。
环比增长率是报告期观察值与前一时期观察值之比减1,说明现象逐期增长变化的程度;
定基增长率是报告期观察值与某一固定时期观察值之比减1,说明现象在整个观察期内总的增长变化程度。
设增长率为G,则环比增长率和定基增长率可表示为:

- 平均增长率
平均增长率也称平均增长速度,它是时间序列中逐期环比值(也称环比发展速度)的几何平均数减1后的结果,计算公式为:
- 增长率分析中应注意的问题
①当时间序列中的观察值出现0或负数时,不易计算增长率。
②在有些情况下。不能单纯就增长率论增长率。要注意将增长率与绝对水平结合起来分析。
增长1%的绝对值表示增长率每增长一个百分点而增加的绝对数量,其计算公式为:
时间序列预测的程序
时间序列分析的一个主要目的就是根据已有的历史数据对未来进行预测。时间序列含有不同的成分,如趋势、季节性、周期性和随机性等。对于一个具体的时间序列,它可能只含有一种成分,也可能同时含有几种成分。含有不同成分的时间序列所用的预测方法是不同的。
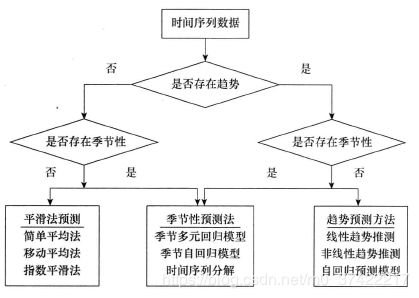
因此,在对时间序列进行预测时,通常包括以下几个步骤:

确定时间序列成分
- 确定趋势成分
确定趋势成分是否存在。
①可以从绘制时间序列的线图入手,从图中可以判断时间序列中是否存在趋势,以及所存在的趋势是线性的还是非线性的。
②判断趋势成分是否存在的另一种方法是利用回归分析拟合一条趋势线,然后对回归系数进行显著性检验。如果回归系数显著,就可以得出线性趋势显著的结论。
- 确定季节成分
确定季节成分可以从绘制时间序列的线图入手,但这里需要一种特殊的时间序列图,即年度折叠时间序列图。绘制该图时,需要将每年的数据分开画在图上,也就是横轴只有一年的长度,每年的数据分别对应纵轴。
举个例子
数据:
年度折叠时间序列图:
如果时间序列只存在季节成分,年度折叠时间序列图中的折线将会有交叉;如果时间序列既含有季节成分又含有趋势,那么年度折叠时间序列图中的折线将不会有交叉,而且如果趋势是上升的,后面年度的折线将会高于前面年度的折线,如果趋势是下降的,则后面年度的折线将低于前面年度的折线。
选择预测方法
预测方法的评估
评价的方法就是找出预测值与实际值的差距。这个差值就是预测误差。最优的预测方法也就是预测误差达到最小的方法。
预测误差的计算方法有几种,包括平均误差、平均绝对误差、均方误差、平均百分比误差和平均绝对百分比误差等。
- 平均误差
设时间序列的第i个观测值为Yi,预测值为Fi,则平均误差可以用ME表示,计算公式为:

式中,n为预测值的个数。
由于预测误差的数值可能有正有负,求和的结果就会相互抵消,在这种情况下,平均误差可能会低估误差。
- 平均绝对误差
平均绝对误差用MAD表示,其计算公式为:

平均绝对误差可以避免误差相互抵消的问题,因而可以准确反映实际预测误差的大小。
- 均方误差
均方误差用MSE表示,其计算公式为:
ME,MAD和MSE的大小受时间序列数据的水平和计量单位的影响,有时并不能真正反映预测模型的好坏,它们只有在比较不同模型对同一数据的预测时才有意义。
- 平均百分比误差和平均绝对百分比误差
平均百分比误差(MPE)和平均绝对百分比误差(MAPE)则消除了时间序列数据的水平和计量单位的影响,是反映误差大小的相对值。
平均百分比误差的计算公式为:
平均绝对百分比误差的计算公式为:
平稳序列的预测
平稳时间序列通常只含有随机成分,其预测方法主要有简单平均法、移动平均法和指数平滑法等,这些方法主要是通过对时间序列进行平滑以消除其随机波动,因而也称为平滑法。
平滑法既可用于对平稳时间序列进行短期预测,也可用于对时间序列进行平滑以描述序列的趋势(包括线性趋势和非线性趋势)。
简单平均法

简单平均法适合对较为平稳的时间序列进行预测.即当时间序列没有趋势时,用该方法比较好。但如果时间序列有趋势或季节成分,该方法的预测则不够准确。此外,简单平均法将远期的数值和近期的数值看作对未来同等重要。但从预测角度看,近期的数值比远期的数值对未来有更大的作用,因此简单平均法预测的结果不够准确。
移动平均法

移动平均法只使用最近k期的数据,在每次计算移动平均值时,移动的间隔都为k。该方法也适合对较为平稳的时间序列进行预测。应用时,关键是确定合理的移动间隔k。对于同一个时间序列,采用不同的移动间隔,预测的准确性是不同的。可通过试验的办法,选择一个使均方误差达到最小的移动间隔。
指数平滑法
指数平滑法是通过对过去的观察值加权平均进行预测的一种方法,该方法使t+1期的预测值等于t期的实际观察值与t期的预测值的加权平均值。指数平滑法是加权平均的一种特殊形式,观察值时间越远,其权数也跟着呈现指数下降,因而称为指数平滑。
一次指数平滑法也称单一指数平滑法,它只有一个平滑系数.而且观察值离预测时期越久远,权数变得越小。
一次指数平滑是将一段时期的预测值与观察值的线性组合作为t+1期的预测值,其预测模型为:
![]()
式中,Yt,为t期的实际观察值,Ft为t期预测值,a为平滑系数(0 在选择 α \alpha α时,还应考虑预测误差,确定 α \alpha α时,可以选择几个值进行预测,然后选择使预测误差最小的值。 时间序列的趋势可以分为线性趋势和非线性趋势两大类. 线性趋势是指现象随着时间的推移而呈现出稳定增长或下降的线性变化规律。 序列中的趋势通常可以认为是由于某种固定的因素作用同一方向所形成的。若这些因素随着时间的推移按线性变化,则可以对时间序列拟合趋势直线;若呈现出某种非线性趋势,则需要拟合适当的趋势曲线。 几种常用的趋势曲线: ②修正指数曲线 修正指数曲线初期增长迅速,随后增长率逐渐降低,最终以K为增长极限。 一般形式: K , b 0 , b 1 K,b_0, b_1 K,b0,b1为待定系数, K > 0 , b 0 ≠ 0 , 0 < b 1 ≠ 1 K>0, b_0 \not= 0, 0< b_1 \neq 1 K>0,b0=0,0<b1=1 ③Gompertz曲线 Gompertz曲线初期增长缓慢,之后逐渐加快,当达到一定程度后,增长率又逐渐下降,最后接近一条水平线。 一般形式: 将等式两边取对数: 等式取对数后,是不是看起来和修正指数曲线的形式很像。 ④多阶曲线 复合型序列是指含有趋势、季节、周期和随机成分的序列。对这类序列的预测方法通常是将时间序列的各个因素依次分解出来,然后进行预测。 分解法预测通常按下面的步骤进行: 季节指数刻画了序列在一个年度内各月或各季度的典型季节特征。在乘法模型中,季节指数是以其平均数等于100%为条件而构成的,它反映了某 第1步:计算移动平均值(如果是季度数据,则采用4项移动平均,月份数据则采用12项移动平均),并对其结果进行中心化处理,也就是将移动平均的结果再进行一次二项移动平均,即得出中心化移动平均值(CMA)。 第2步:计算移动平均的比值,也称为季节比率,即将序列的各观察值除以相应的中心化移动平均值,然后计算出各比值的季度(或月份)平均值。 第3步:季节指数调整。由于各季节指数的平均数应等于1,若根据第2步计算的季节比率的平均值不等于1,则需要进行调整。具体方法是:将第2步算的每个季节比率的平均值除以它们的总平均值。 对消除季节成分的序列建立适当的预测模型,并根据这一模型进行预测。 用预测值乘以相应的季节指数,得到最终的预测值。
使用指数平滑法时,关键的问题是确定一个合适的平滑系数α,因为不同的α会对预测结果产生不同的影响。例如.当α=0时,预测值仅仅是重复上一期的预测结果;当α=1时,预测值就是上一期实际值。α越接近1,模型对时间序列变化的反应就越及时,因为它给当前的实际值赋予了比预测值更大的权数。同样,α越接近0.意味着给当前的预测值赋予了更大的权数,因此模型对时间序列变化的反应就越慢。
一般而言,当时间序列有较大的随机波动时,宜选较大的α,以便能很快跟上近期的变化;当时间序列比较平稳时,宜选较小的α。
趋势型序列的预测
线性趋势预测
非线性趋势预测
①指数曲线
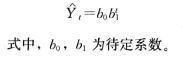
采取线性化手段将其化为对数直线形式,即两端取对数得:
![]()
然后根据最小二乘法原理,按直线形式的常数确定方法。得到求解lgb0和lgb1的标准方程如下:
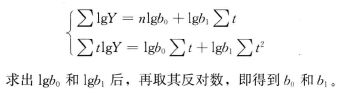
Y t ^ = K + b 0 b 1 t \hat{Y_t}=K+b_0 b_1^t Yt^=K+b0b1t
Y t ^ = K b 0 b 1 t \hat{Y_t} = Kb_0^{b_1^t} Yt^=Kb0b1t
K , b 0 , b 1 K,b_0, b_1 K,b0,b1为待定系数, K > 0 , 0 < b 0 ≠ 0 , 0 < b 1 ≠ 1 K>0,0 < b_0 \not= 0, 0< b_1 \not= 1 K>0,0<b0=0,0<b1=1
l g Y t ^ = l g K + ( l g b 0 ) b 1 t lg \hat{Y_t} = lgK + (lgb_0)b_1^t lgYt^=lgK+(lgb0)b1t
复合型序列的分解预测
确定并分离季节成分
一月份或季度的数值占全年平均数值的大小。
将季节成分从时间序列中分离出去,即用每一个观测值除以相应的季节指数,以消除季节性。季节因素分离后的序列,反映了没有季节因素影响下时间序列的变化形态。建立预测模型并进行预测
计算出最后的预测值