[论文笔记] ElasticFusion: Dense SLAM Without A Pose Graph

一、overview

提出了一种密集SLAM方法，使用RGBD数据，进行跟踪和建图。
主要贡献：

1. surfel-based稠密建图。
2. 将surfel分为激活区域和非激活区域，一段时间内未观测到的归入非激活区域。
3. 每一帧，尝试把激活模型中当前相机估测位姿部分，登记至非激活模型在当前帧的部分，若登记成功，则检测到闭环，进行非刚体变换。发生闭环的非激活部分再次激活，放入登记的区域。（感觉意思是每一帧把同视角下的激活部分和未观测到的非激活部分匹配，来检测闭环）。
4. 对于全局闭环，向随机encoding database里添加预测视角，每一帧匹配这个视角，如果匹配到，就登记这个视角并检测是否全局一致。如果是，对地图进行非刚体变换，消除闭环，（这个不太懂，predicted view是估计的位姿吗？根据估计位姿的匹配来检测和消除闭环？）

文章用词和以前看的都不太一样，读起来不太容易。frame-to-model和model-to-model应该分别是相机位姿估计和地图构建的优化。registration可能是做匹配的意思。

文章先提出了registration的方法，用于做跟踪。使用的是几何+光度联合误差优化。但是不知道激活和非激活在匹配中具体是怎么用的？
还提出了两个闭环检测。得到闭环后的优化使用了形变图。

二、fused predicted tracking

地图使用surfel表示。在做估测时：

1. 同时预测深度图和彩色图，用于几何和光度的模型tracking。
2. 将surfel根据未观测到的时间间隔，分为激活的和非激活的。设置时间间隔阈值。仅用激活的surfel进行相机位姿估计和深度图融合。
   每一帧估计相机的全局位姿，方法是匹配(register)当前帧深度图和彩色图，与上一帧估计相机位姿下激活模型的深度图和彩色图。

2.1. geometric pose estimation

几何误差针对深度图，error是在surfel表示中的顶点vertex中计算。
使用point-to-plane error:
$$E_{icp}=\sum _k((v^k-exp(e)T{v}_t^k)n^k{)}^2$$
$v_t^k$是当前帧的第$k$个点，$T$是当前帧和上一帧的变换估测，$v^k$和$n^k$是上一帧的匹配顶点和法线。
优化目标是$exp(e)$里的motion parameter $e$，这里不太懂李代数到李群的映射，不过这个point to plane error在很多地方都有用到，之后看看这个论文。

2.2. photometric pose estimation

光度误差针对彩色图（强度图），误差是在像素中计算。

$$E=\sum _u(I(u,c_t^l)-I(\pi (Kexp(e)Tp(u,D_t^l),c_{t-1}^a){)}^2$$
$c$是彩色图，$u$是像素坐标，$I(u,c)$是取彩色图中对应坐标的强度值。$p(u,d)$是取深度图中对应坐标的3D back projection，即当前帧相机坐标系下的三维坐标，经过T转换到上一帧的相机坐标系下，乘以内参K到像素平面，经过$\pi$转换成2d坐标。
因此计算的是每一个像素位置，当前帧和根据模型估测位姿，对应上一帧的像素差值。
同一坐标，在这一帧和上一帧中，经估计的位姿转换后的强度差值。

2.3. Joint Optimisation

最小化联合cost：
$$E_{track}=E_{icp}+w_{rgb}{E}_{rgb}$$
求其jacobian，构造最小二乘形式，使用高斯牛顿法优化最小二乘问题。
使用了三层的金字塔结构来迭代求解。

三、 Deformation Graph

使用surfel级的表面闭环检测来实现局部和全局的一致性。模型表面闭环检测通过对于所有surfel（激活和非激活的）进行非刚体形变来进行，非刚体形变的依据是表面约束（surface constraints）。
具体方法是，基于surfel构造一个形变图(deformation graph)，通过优化形变图来进行surfel的调整，从而进行模型表面的形变。
图由节点和边构成：
节点包括：

• 时间戳
• 位姿($G_g^n\in R^3$)
• 一组邻居点($N(g^n)$)，每个节点的邻居点数固定为$k$
• 旋转矩阵（$g_R^n$）
• 平移向量（$g_t^n$）

边：
当前节点和它的邻居之间连边

要优化的就是$g_R^n$和$g_t^n$，通过这两个转移量，实现模型表面的变。
每一个surfel $M^s$定义了一组受影响的节点$I(M^s,g)$。通过这些节点计算形变后的surfel位置和法向。
位置形变：

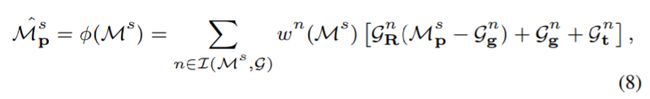
对于与这个surfel相关的所有节点，计算surfel位置和节点位置差值，乘以节点的旋转矩阵，加上节的位置和平移向量，再乘以系数。

法向形变：

这里每个求和里的系数是上一个节点的旋转矩阵？

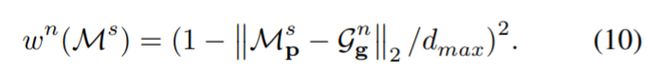
前面那个系数代表的是这个surfel的节点权重，节点和surfel位置越相近，权重越大。$d_{m}ax$是这个surfel k个最近点的欧几里得距离。

3.1. construction

这一节描述了如何在每一帧建一个形变图。
使用systematic sampling采样法，从所有surfel均匀采样$|g|$个，形变图的节点数远少于surfel数。初始化时，节点的位置和时间戳与采样来源的surfel相同。节点按照初始时间戳排序，其邻居节点的确定是根据排序结果找左右的K个。

3.2. application

这一节讲了得到形变图后，怎么找出用于更新每个surfel的节点，并且如何更新surfel。

1. 先根据时间戳找到最接近当前surfel的节点，这里用二分搜索
2. 根据时间戳排序，找$\alpha$个最相近的节点
3. 从这些节点中，根据欧几里得距离，找k个距离最近的点，这些点就是$I(M^s,g)$
4. 按照上面的方法计算权重、位置更新、法向更新，得到更新后的surfel

3.3. optimisation

这节将了怎么优化节点的旋转和平移量。
首先定义了一个元组Q，描述的是点在形变过程中的变化，包含点的起始位置、终点位置、起始时间戳、终点时间戳。
优化过程，定义了四个cost：

• $E_{rot}$：目的是最大化形变的刚体性。
• $E_{reg}$：正则项，目的是确保形变的平滑。
• $E_{con}$：限制项，目的是最小化形变后的误差，就是让点在形变后尽可能接近终点。
• $E_{pin}$：目的是固定地图模型的非激活区域，形变激活区域的模型到非激活坐标系？

然后就最小化这四个cost的加权和。
具体cost怎么定义的不太懂。

四、 Local Loop Closure

这部分是进行局部闭环。构建地图模型的surfel有一个标签：激活/非激活。tracking的时候只使用激活的surfel。当一定时间内没有 观测到一个surfel，就把它的标签置为非激活。
在同一视角下看模型，可能存在对于同一个场景，分别设成了激活和非激活，这样就产生了偏移。局部闭环检测就是为了消除这些偏移。
消除闭环的方法是上面说的使用形变图优化，优化的时候，上面提到了所用的限制元组Q，这一节就是讲了怎么在局部闭环中确定Q。
现有当前位姿估计$p_t$（这应该是地图中surfel的估计），要通过闭环检测，得到一个转移矩阵$H\in {SE}_3$，来对齐激活模型部分和非激活模型部分。
首先对当前帧进行注册（registration process）
根据注册过程中的高斯优化结果，判断是否闭环。判断依据有：

• 优化过程中的误差足够小
• 内点足够多
• 协方差矩阵的特征值

如果满足条件，就生成一组Q。方法是均匀采样一些像素点，根据深度图和时间戳得到相应Q。

最终得到用于对齐模型的转移矩阵H。非激活区域的点再次激活，并用于tracking。

五、 Global Loop Closure

全局闭环检测使用randomised fern encoding方法，是一种基于RGBD图像的识别方法，应该和词袋的思想差不多，在运行过程中同步简历数据库和匹配。
每一帧进行下采样，然后计算得到一个描述串，和一切其他属性共同构成它的帧元素。然后每帧对它和数据库中的帧元素匹配，看这个地方有没有来过。

若匹配到，和局部闭环流程一样。

• 先进行寄存，应该是对当前帧和匹配帧做匹配。
• 根据高斯优化结果计算是否闭环
• 若闭环，得到转移矩阵H
• 采样计算模型表面限制Q
• 输入形变图，进行surfel优化