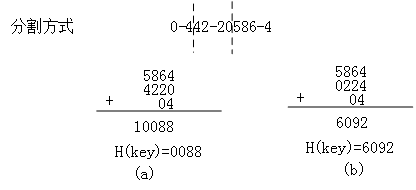哈希表基本概念介绍及哈希冲突的处理方法(附源码)
工科生一枚,热衷于底层技术开发,有强烈的好奇心,感兴趣内容包括单片机,嵌入式Linux,Uboot等,欢迎学习交流!
爱好跑步,打篮球,睡觉。 欢迎加我QQ1500836631(备注CSDN),一起学习交流问题,分享各种学习资料,电子书籍,学习视频等。
文章目录
- 哈希表和哈希函数的概念
- 哈希函数的构造
- 直接定址法
- 数字分析法
- 平方取中法
- 折叠法
- 除留余数法(常用)
- 随机数法
- 哈希函数的选择
- 处理冲突的方法
- 开放定址法
- 再哈希法
- 链地址法
- 建立一个公共溢出区
- 代码实现
哈希表和哈希函数的概念
哈希表(散列表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做哈希(散列)函数,存放记录的数组叫做哈希(散列)表。
给定表M,存在函数f(key),对任意给定的关键字值key,代入函数后若能得到包含该关键字的记录在表中的地址,则称表M为哈希(Hash)表,函数f(key)为哈希(Hash) 函数。
数据的哈希地址=f(关键字的值)。
哈希地址只是表示在查找表中的存储位置,而不是实际的物理存储位置。f()是一个函数,通过这个函数可以快速求出该关键字对应的的数据的哈希地址,称之为“哈希函数”。
哈希函数的构造
直接定址法
取关键字或关键字的某个线性函数值为散列地址。即H(key)=key或H(key) = a·key + b,其中a和b为常数(这种散列函数叫做自身函数)。若其中H(key)中已经有值了,就往下一个找,直到H(key)中没有值了,就放进去。
例如有一个从 1 岁到 100 岁的人口数字统计表

假设其哈希函数为第一种形式,其关键字的值表示最终的存储位置。若需要查找年龄为 25 岁的人口数量,将年龄 25 带入哈希函数中,直接求得其对应的哈希地址为 25(求得的哈希地址表示该记录的位置在查找表的第 25 位)。一般用数组实现。
数字分析法
如果关键字由多位字符或者数字组成,就可以考虑抽取其中的 2 位或者多位作为该关键字对应的哈希地址,在取法上尽量选择变化较多的位,避免冲突发生。
比如一组员工的出生年月日,这时我们发现出生年月日的前几位数字大体相同,这样的话,出现冲突的几率就会很大,但是我们发现年月日的后几位表示月份和具体日期的数字差别很大,如果用后面的数字来构成散列地址,则冲突的几率会明显降低。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
平方取中法
对关键字做平方操作,取中间得几位作为哈希地址。此方法也是比较常用的构造哈希函数的方法。
例如关键字序列为{421,423,436},对各个关键字进行平方后的结果为{177241,178929,190096},则可以取中间的两位{72,89,00}作为其哈希地址。
折叠法
例如,在图书馆中图书都是以一个 10 位的十进制数字为关键字进行编号的,若对其查找表建立哈希表时,就可以使用折叠法。
若某书的编号为:0-442-20586-4,分割方式如图 1 中所示,在对其进行折叠时有两种方式:一种是移位折叠,另一种是间界折叠:
- 移位折叠是将分割后的每一小部分,按照其最低位进行对齐,然后相加,如下图 (a);
- 间界折叠是从一端向另一端沿分割线来回折叠,如下图(b)。
除留余数法(常用)
取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p,p<=m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。
对p的选择很重要,一般取素数或m,若p选的不好,容易产生同义词(即冲突)。
由经验得知 p 可以为不大于 m 的质数或者不包含小于 20 的质因数的合数。
随机数法
取关键字的一个随机函数值作为它的哈希地址,即:
H(key)=random(key),此方法适用于关键字长度不等的情况。
注意:这里的随机函数其实是伪随机函数,随机函数是即使每次给定的 key 相同,但是 H(key)都是不同;而伪随机函数正好相反,每个 key 都对应的是固定的 H(key)。
哈希函数的选择
如此多的构建哈希函数的方法,在选择的时候,需要根据实际的查找表的情况采取适当的方法。通常考虑的因素有以下几方面:
- 关键字的长度。如果长度不等,就选用随机数法。如果关键字位数较多,就选用折叠法或者数字分析法;反之如果位数较短,可以考虑平方取中法;
- 哈希表的大小。如果大小已知,可以选用除留余数法;
- 关键字的分布情况;
- 查找表的查找频率;
- 计算哈希函数所需的时间(包括硬件指令的因素)
处理冲突的方法
哈希冲突只能尽量减少但是不能完全避免了,通常处理哈希冲突的方法有以下几种
开放定址法
H(key)=(H(key)+ d)MOD m(其中 m 为哈希表的表长,d 为一个增量)
当得出的哈希地址产生冲突时,选取以下 3 种方法中的一种获取 d 的值,然后继续计算,直到计算出的哈希地址不在冲突为止,这 3 种方法为:
- 线性探测法:d=1,2,3,…,m-1
- 二次探测法:d=12,-12,22,-22,32,…
- 伪随机数探测法:d=伪随机数
例如,在长度为 11 的哈希表中已填写好 17、60 和 29 这 3 个数据(如图(a) 所示),其中采用的哈希函数为:H(key)=key MOD 11,现有第 4 个数据 38 ,当通过哈希函数求得的哈希地址为 5,与 60 冲突,则分别采用以上 3 种方式求得插入位置如图 (b)所示:
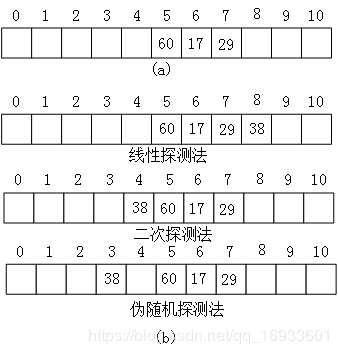
注释:在线性探测法中,当遇到冲突时,从发生冲突位置起,每次 +1,向右探测,直到有空闲的位置为止;二次探测法中,从发生冲突的位置起,按照 +12,-12,+22,…如此探测,直到有空闲的位置;伪随机探测,每次加上一个随机数,直到探测到空闲位置结束。
再哈希法
当通过哈希函数求得的哈希地址同其他关键字产生冲突时,使用另一个哈希函数计算,直到冲突不再发生。
链地址法
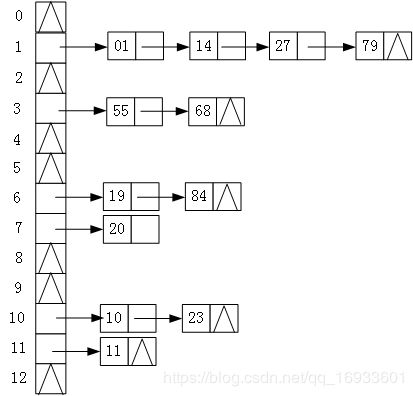
将所有产生冲突的关键字所对应的数据全部存储在同一个线性链表中。例如有一组关键字为{19,14,23,01,68,20,84,27,55,11,10,79},其哈希函数为:H(key)=key MOD 13,使用链地址法所构建的哈希表如下图 所示:
建立一个公共溢出区
建立两张表,一张为基本表,另一张为溢出表。基本表存储没有发生冲突的数据,当关键字由哈希函数生成的哈希地址产生冲突时,就将数据填入溢出表。
代码实现
在哈希表中进行查找的操作同哈希表的构建过程类似,其具体实现思路为:对于给定的关键字K,将其带入哈希函数中,求得与该关键字对应的数据的哈希地址,如果该地址中没有数据,则证明该查找表中没有存储该数据,查找失败:如果哈希地址中有数据,就需要做进一步的证明(排除冲突的影响),找到该数据对应的关键字同K 进行比对,如果相等,则查找成功;反之,如果不相等,说明在构造哈希表时发生了冲突,需要根据构造表时设定的处理冲突的方法找到下一个地址,同地址中的数据进行比对,直至遇到地址中数据为NULL(说明查找失败),或者比对成功。
/*
* @Author: Carlos
* @Date: 2020-07-2 23:48:50
* @LastEditTime: 2020-07-2 23:48:50
* @LastEditors: Carlos
* @Description: Hash
*/
#include "stdio.h"
#include "stdlib.h"
#define HASHSIZE 7 //定义散列表长为数组的长度
#define NULLKEY -1
typedef struct
{
int *elem; //数据元素存储地址,动态分配数组
int count; //当前数据元素个数
} HashTable;
/**
* @Description: 哈希函数初始化
* @Param: HashTable *hashTable 结构体指针
* @Return: 无
* @Author: Carlos
*/
void Init(HashTable *hashTable)
{
int i;
hashTable->elem = (int *)malloc(HASHSIZE * sizeof(int));
hashTable->count = HASHSIZE;
for (i = 0; i < HASHSIZE; i++)
{
hashTable->elem[i] = NULLKEY;
}
}
/**
* @Description: 哈希函数(除留余数法)
* @Param: int data 哈希的数据
* @Return: 哈希后data存储的地址
* @Author: Carlos
*/
int Hash(int data)
{
return data % HASHSIZE;
}
/**
* @Description: 哈希表的插入函数,可用于构造哈希表
* @Param: HashTable *hashTable 结构体指针,int data 哈希的数据
* @Return: 无
* @Author: Carlos
*/
void Insert(HashTable *hashTable, int data)
{
int hashAddress = Hash(data); //求哈希地址
//发生冲突
while (hashTable->elem[hashAddress] != NULLKEY)
{
//利用开放定址法解决冲突
hashAddress = (++hashAddress) % HASHSIZE;
}
hashTable->elem[hashAddress] = data;
}
/**
* @Description: 哈希表的查找算法
* @Param: HashTable *hashTable 结构体指针,int data 哈希的数据
* @Return: 无
* @Author: Carlos
*/
int Search(HashTable *hashTable, int data)
{
int hashAddress = Hash(data); //求哈希地址
while (hashTable->elem[hashAddress] != data)
{ //发生冲突
//利用开放定址法解决冲突
hashAddress = (++hashAddress) % HASHSIZE;
//如果查找到的地址中数据为NULL,或者经过一圈的遍历回到原位置,则查找失败
if (hashTable->elem[hashAddress] == NULLKEY || hashAddress == Hash(data))
{
return -1;
}
}
return hashAddress;
}
int main()
{
int i, result;
HashTable hashTable;
int arr[HASHSIZE] = {13, 29, 27, 28, 26, 30, 38};
//初始化哈希表
Init(&hashTable);
//利用插入函数构造哈希表
for (i = 0; i < HASHSIZE; i++)
{
Insert(&hashTable, arr[i]);
}
//调用查找算法
result = Search(&hashTable, 29);
if (result == -1)
printf("查找失败");
else
printf("29 在哈希表中的位置是:%d", result + 1);
return 0;
}