TDOA定位方法的Fang算法的程序实现(二维)
TDOA定位方法的Fang算法的程序实现(二维)
摘要:
蜂窝无线定位服务(LCS)是一种具有广阔市场前景的移动增值业务,其基本原理是利用现有蜂窝网络,通过对各种位置特征参数,包括到达时间(TOA),到达时间差(TDOA),到达方向(DOA)的测量和估计,从而实现移动用户的定位。
本篇介绍TDOA定位方法的Fang算法及其程序实现。
1、引言:
在各种无线定位系统中,采用的基本定位方法和技术都是相同或者相似的。
从几何角度讲,确定目标在二维或者三维空间的位置可以由两个或者多个曲线在二维或者三维空间内相交得到,以这一标准进行划分,可供选择的定位方法有:
1:圆周定位方法
2:双曲线定位方法
3:方位角测量定位方法
4:混合定位方法
一般,基于电磁波场强和TOA的定位采用的是圆周定位。基于AOA采用的是方位角定位。基于TDOA的定位是采用双曲线定位,混合定位则是基于AOA、TDOA或者其他组合。
2、TDOA双曲线模型


根据上面的方程组,进而可以求解得到移动台MS的位置坐标。
不管是哪种TDOA的双曲线算法(熟知的如Chan 或者Fang),在二维平面中,只需要三个基站就可以定位出移动台MS的XY坐标。
如果是三维空间中,需要四个基站才可以定位出MS的XYZ坐标。
3、Fang 算法原理

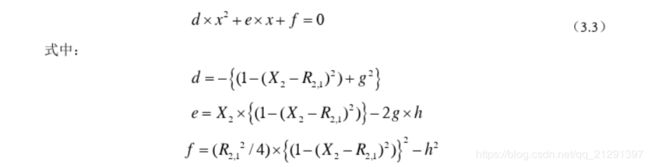
解方程(3.3),可以得到两个X值,,利用有关先验信息如(标签得到两个基站的距离差R21),就可以取到正确的X值。然后利用式(3.2)得到Y值。
4、代码实现
这里我们用C++做程序实现:
这里我们先预设了3个基站、及标签T到基站的距离
//基站1--基站3坐标
double AncLoc[3][3]={
{0,0,0},
{700,0,0},
{700,740,0},
// {30,740,300},
};
//标签到3个基站的距离
double T2A_R[3] = {671,506,351};
主函数
int main(int argc, char** argv) {
FangTDOA Anc; //创建对象
Anc.GetAncData(&AncLoc[0][0],3,3); //获取基站坐标
Anc.displayAncData(); //显示基站坐标
Anc.getRang(&T2A_R[0]); //获取标签到基站的距离
Anc.displayATrang(); //显示标签到基站的距离
Anc.DeviationRang(1); //计算标签到基站的距离差
Anc.get3gh(); //计算得到参数g,h
Anc.get3def(); //计算得到参数d,e,f
Anc.getX(); //得到X坐标
Anc.getY(); //得到Y坐标
Anc.checkResult(); //得到最终坐标点
return 0;
}
主要关键代码:
#include 结果输出:
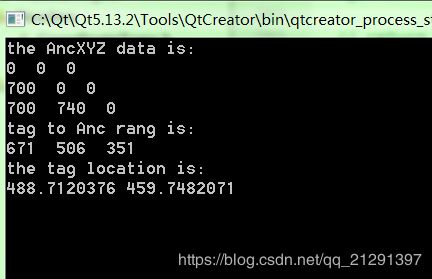
相关参考代码详见附件
//download.csdn.net/download/qq_21291397/12103237
PS:
1、Fang 算法,相对Chan 算法相对复杂,而且对基站的参数有一定的限制,如果基站的坐标可任意设定,这里还需要通过坐标变换(平移和旋转)来实现。
2、三维Fang算法,也可以进一步实现:可以参考下面一片文章:
http://www.doc88.com/p-7724949260733.html,可惜该论文有很多印刷的错误,部分公式的推导也是错误的。但思路可以借鉴。