西瓜书——第三章课后习题

题3.1

试析在什么情况下f(x)=w^(T)+b中不必考虑偏置项b

首先要知道为什么要加偏置项？它的作用是什么？在之前学过的一次函数中，b其实就是函数在y轴的截距，控制着函数偏离原点的距离，那么在线性模型中应该也是类似作用。看了这个博主的文章，大概意思就是加偏置项是为了更好的拟合数据。

其实我自己看到这个题第一反应是，如果让 fi-fj，这样就可以消掉b了，自然也就不用考虑它。也就是让所有数据集都和任意一个数据集相减，最后得到一个新的数据模型f(x)’=w^(T)。

但是又感觉不是这样的吧，莫名心虚，就有去看别人的回答主要有两种答案，感觉都很有道理：

• ①在f(x)进行归一化处理时消除偏置，具体方法在这里
• ②当只需要考虑x的取值对y的影响的话，则可以不用考虑b。

题3.2

试证明，对于参数w,对率回归的目标函数(3.18)是非凸的，但其对数似然函数（3.27）是凸的。

题3.3

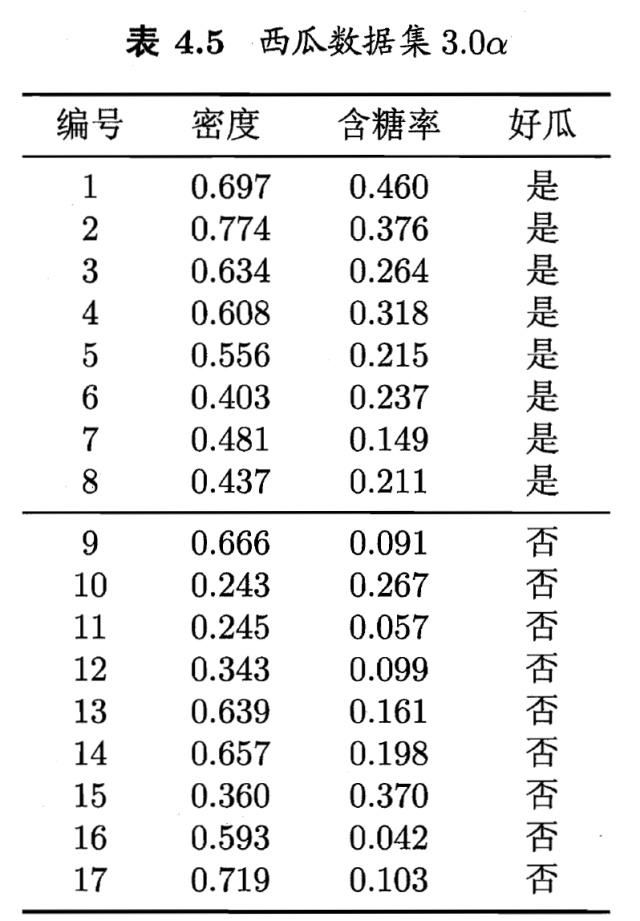
编程实现对率回归，并给西瓜数据集3.0a上的结果。

import numpy as np
import math
import matplotlib.pyplot as plt

data_x = [[0.697, 0.460], [0.774, 0.376], [0.634, 0.264], [0.608, 0.318], [0.556, 0.215], [0.403, 0.237],
          [0.481, 0.149], [0.437, 0.211],[0.666, 0.091], [0.243, 0.267], [0.245, 0.057], [0.343, 0.099], 
          [0.639, 0.161], [0.657, 0.198],[0.360, 0.370], [0.593, 0.042], [0.719, 0.103]
         ]
data_y = [1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]

def combine(beta, x):
    x = np.mat(x + [1.]).T
    return beta.T * x

def predict(beta, x):
    return 1 / (1 + math.exp(-combine(beta, x)))

def p1(beta, x):
    return math.exp(combine(beta, x)) / (1 + math.exp(combine(beta, x)))

beta = np.mat([0.] * 3).T

steps = 50

for step in range(steps):
    param_1 = np.zeros((3, 1))
    for i in range(len(data_x)):
        x = np.mat(data_x[i] + [1.]).T
        param_1 = param_1 - x * (data_y[i] - p1(beta, data_x[i]))
    param_2 = np.zeros((3, 3))
    for i in range(len(data_x)):
        x = np.mat(data_x[i] + [1.]).T
        param_2 = param_2 + x * x.T * p1(beta, data_x[i]) * (1 - p1(beta, data_x[i]))
    last_beta = beta
    beta = last_beta - param_2.I * param_1
    if np.linalg.norm(last_beta.T - beta.T) < 1e-6:
        print(step)
        break

for i in range(len(data_x)):
    if data_y[i] == 1:
        plt.plot(data_x[i][0], data_x[i][1], 'ob')
    else:
        plt.plot(data_x[i][0], data_x[i][1], '^g')
w_0 = beta[0, 0]
w_1 = beta[1, 0]
b = beta[2, 0]
print(w_0, w_1, b)
x_0 = -b / w_0 #(x_0, 0)
x_1 = -b / w_1 #(0, x_1)
plt.plot([x_0, 0], [0, x_1])
plt.show()

题3.5

编程实现线性判别分析，并给出西瓜数据集3.0a上的结果。

import numpy as np
import math
import matplotlib.pyplot as plt

data_x = [[0.697, 0.460], [0.774, 0.376], [0.634, 0.264], [0.608, 0.318], [0.556, 0.215], [0.403, 0.237],
          [0.481, 0.149], [0.437, 0.211],
          [0.666, 0.091], [0.243, 0.267], [0.245, 0.057], [0.343, 0.099], [0.639, 0.161], [0.657, 0.198],
          [0.360, 0.370], [0.593, 0.042], [0.719, 0.103]]
data_y = [1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]

mu_0 = np.mat([0., 0.]).T
mu_1 = np.mat([0., 0.]).T
count_0 = 0
count_1 = 0
for i in range(len(data_x)):
    x = np.mat(data_x[i]).T
    if data_y[i] == 1:
        mu_1 = mu_1 + x
        count_1 = count_1 + 1
    else:
        mu_0 = mu_0 + x
        count_0 = count_0 + 1
mu_0 = mu_0 / count_0
mu_1 = mu_1 / count_1

S_w = np.mat([[0, 0], [0, 0]])
for i in range(len(data_x)):
    # 注意：西瓜书的输入向量是列向量形式
    x = np.mat(data_x[i]).T
    if data_y[i] == 0:
        S_w = S_w + (x - mu_0) * (x - mu_0).T
    else:
        S_w = S_w + (x - mu_1) * (x - mu_1).T

u, sigmav, vt = np.linalg.svd(S_w)
sigma = np.zeros([len(sigmav), len(sigmav)])
for i in range(len(sigmav)):
    sigma[i][i] = sigmav[i]
sigma = np.mat(sigma)
S_w_inv = vt.T * sigma.I * u.T
w = S_w_inv * (mu_0 - mu_1)

w_0 = w[0, 0]
w_1 = w[1, 0]
tan = w_1 / w_0
sin = w_1 / math.sqrt(w_0 ** 2 + w_1 ** 2)
cos = w_0 / math.sqrt(w_0 ** 2 + w_1 ** 2)

print(w_0, w_1)

for i in range(len(data_x)):
    if data_y[i] == 0:
        plt.plot(data_x[i][0], data_x[i][1], "go")
    else:
        plt.plot(data_x[i][0], data_x[i][1], "b^")

plt.xlabel('x')
plt.ylabel('y')
plt.title('Linear Discriminant Analysis')
plt.plot(mu_0[0, 0], mu_0[1, 0], "ro")
plt.plot(mu_1[0, 0], mu_1[1, 0], "r^")
plt.plot([-0.1, 0.1], [-0.1 * tan, 0.1 * tan])

for i in range(len(data_x)):
    x = np.mat(data_x[i]).T
    ell = w.T * x
    ell = ell[0, 0]
    if data_y[i] == 0:
        plt.scatter(cos * ell, sin * ell, marker='o', c='', edgecolors='g')
    else:
        plt.scatter(cos * ell, sin * ell, marker='^', c='', edgecolors='b')
plt.show()