【JAVA】力扣第198场周赛代码+解题思路——【排名第 1 ~ 300 名的参赛者可获「微软中国」简历内推机会】做对前两道就能排到268/ 5778(4.6%)
目录
- 前言
- 一、题目:5464. 换酒问题
- 题解
- 代码
- 二、题目:5465. 子树中标签相同的节点数
- 题解
- 代码
- 三、题目:5466. 最多的不重叠子字符串
- 题解
- 代码
- 四、5467. 找到最接近目标值的函数值
- 题解
- 代码
前言

【工作机会奖励】
排名第 1 ~ 300 名的参赛者可获「微软中国」简历内推机会
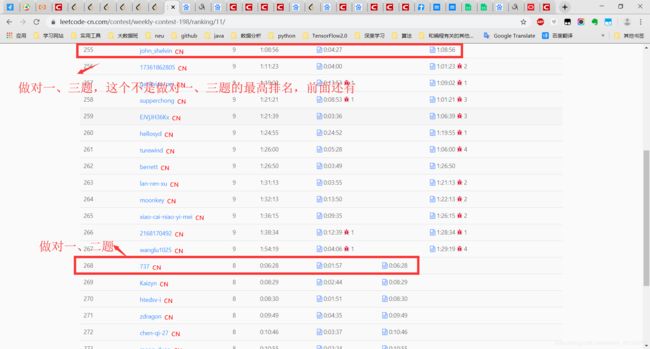
做对第一、二道,就能排到268/ 5778(4.6%),如果是做对其他的两道,那么排名更高,比如一、三,一、四,三、四,也就是说,你只要会两道,就可以得到微软的简历内推机会!!!!
一、题目:5464. 换酒问题
通过的用户数4285
尝试过的用户数4367
用户总通过次数4334
用户总提交次数5951
题目难度Easy
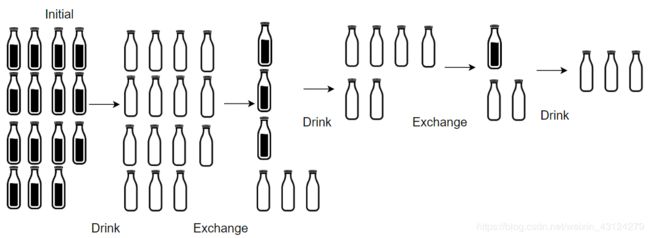
小区便利店正在促销,用 numExchange 个空酒瓶可以兑换一瓶新酒。你购入了 numBottles 瓶酒。
如果喝掉了酒瓶中的酒,那么酒瓶就会变成空的。
请你计算 最多 能喝到多少瓶酒。
输入:numBottles = 9, numExchange = 3
输出:13
解释:你可以用 3 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 9 + 3 + 1 = 13 瓶酒。
输入:numBottles = 15, numExchange = 4
输出:19
解释:你可以用 4 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 15 + 3 + 1 = 19 瓶酒。
示例 3:
输入:numBottles = 5, numExchange = 5
输出:6
示例 4:
输入:numBottles = 2, numExchange = 3
输出:2
提示:
1 <= numBottles <= 1002 <= numExchange <= 100
题解
代码
class Solution {
public int numWaterBottles(int numBottles, int numExchange) {
int num=0,emptyBottles=0;
while(numBottles>0) {
num+=numBottles;
emptyBottles+=numBottles;
numBottles=emptyBottles/numExchange;
emptyBottles=emptyBottles%numExchange;
}
return num;
}
}
二、题目:5465. 子树中标签相同的节点数
通过的用户数998
尝试过的用户数2651
用户总通过次数1007
用户总提交次数6917
题目难度Medium
给你一棵树(即,一个连通的无环无向图),这棵树由编号从 0 到 n - 1 的 n 个节点组成,且恰好有 n - 1 条 edges 。树的根节点为节点 0 ,树上的每一个节点都有一个标签,也就是字符串 labels 中的一个小写字符(编号为 i 的 节点的标签就是 labels[i] )
边数组 edges 以 edges[i] = [ai, bi] 的形式给出,该格式表示节点 ai 和 bi 之间存在一条边。
返回一个大小为 n 的数组,其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。
树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。
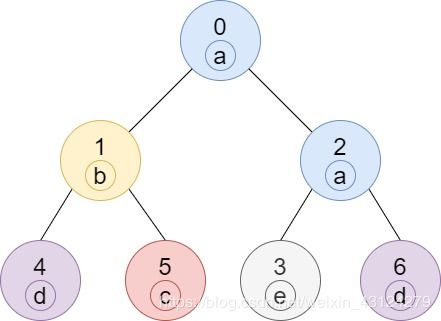
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
输出:[2,1,1,1,1,1,1]
解释:节点 0 的标签为 'a' ,以 'a' 为根节点的子树中,节点 2 的标签也是 'a' ,因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 'b' ,节点 1 的子树包含节点 1、4 和 5,但是节点 4、5 的标签与节点 1 不同,故而答案为 1(即,该节点本身)。
输入:n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
输出:[4,2,1,1]
解释:节点 2 的子树中只有节点 2 ,所以答案为 1 。
节点 3 的子树中只有节点 3 ,所以答案为 1 。
节点 1 的子树中包含节点 1 和 2 ,标签都是 'b' ,因此答案为 2 。
节点 0 的子树中包含节点 0、1、2 和 3,标签都是 'b',因此答案为 4 。
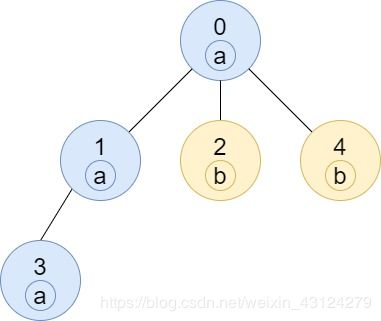
输入:n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
输出:[3,2,1,1,1]
示例 4:
输入:n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa"
输出:[1,2,1,1,2,1]
示例 5:
输入:n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa"
输出:[6,5,4,1,3,2,1]
提示:
1 <= n <= 10^5edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != bilabels.length == nlabels 仅由小写英文字母组成
题解
代码
class Solution {
public int[] countSubTrees(int n, int[][] edges, String labels) {
List<List<Integer>> neighbors=new ArrayList<>();
List<HashMap<Character, Integer>> list=new ArrayList<>();
for(int i=0;i<n;i++){
neighbors.add(new ArrayList<>());
list.add(new HashMap<>());
}
for(int i=0;i<edges.length;i++){
neighbors.get(edges[i][0]).add(edges[i][1]);
neighbors.get(edges[i][1]).add(edges[i][0]);
}
boolean[] arr=new boolean[n];
dfs(0,neighbors,list,labels,arr);
int[] result=new int[n];
for(int i=0;i<n;i++){
result[i]=list.get(i).get(labels.charAt(i));
}
return result;
}
private void dfs(int root, List<List<Integer>> neighbors, List<HashMap<Character, Integer>> list, String labels, boolean[] arr) {
arr[root]=true;
list.get(root).put(labels.charAt(root), 1);
for(int neighbor:neighbors.get(root)) {
if(arr[neighbor]) continue;
dfs(neighbor, neighbors, list, labels, arr);
for(char c:list.get(neighbor).keySet()) {
list.get(root).put(c, list.get(root).getOrDefault(c, 0)+list.get(neighbor).get(c));
}
}
}
}
三、题目:5466. 最多的不重叠子字符串
通过的用户数161
尝试过的用户数675
用户总通过次数165
用户总提交次数1640
题目难度Medium
给你一个只包含小写字母的字符串 s ,你需要找到 s 中最多数目的非空子字符串,满足如下条件:
这些字符串之间互不重叠,也就是说对于任意两个子字符串 s[i…j] 和 s[k…l] ,要么 j < k 要么 i > l 。
如果一个子字符串包含字符 c ,那么 s 中所有 c 字符都应该在这个子字符串中。
请你找到满足上述条件的最多子字符串数目。如果有多个解法有相同的子字符串数目,请返回这些子字符串总长度最小的一个解。可以证明最小总长度解是唯一的。
请注意,你可以以 任意 顺序返回最优解的子字符串。
示例 1:
输入:s = "adefaddaccc"
输出:["e","f","ccc"]
解释:下面为所有满足第二个条件的子字符串:
[
"adefaddaccc"
"adefadda",
"ef",
"e",
"f",
"ccc",
]
如果我们选择第一个字符串,那么我们无法再选择其他任何字符串,所以答案为 1 。如果我们选择 "adefadda" ,剩下子字符串中我们只可以选择 "ccc" ,它是唯一不重叠的子字符串,所以答案为 2 。同时我们可以发现,选择 "ef" 不是最优的,因为它可以被拆分成 2 个子字符串。所以最优解是选择 ["e","f","ccc"] ,答案为 3 。不存在别的相同数目子字符串解。
示例 2:
输入:s = "abbaccd"
输出:["d","bb","cc"]
解释:注意到解 ["d","abba","cc"] 答案也为 3 ,但它不是最优解,因为它的总长度更长。
提示:
1 <= s.length <= 10^5s 只包含小写英文字母。
题解
代码
class Solution {
public List<String> maxNumOfSubstrings(String s) {
int[][] index=new int[26][2];
for(char i='a';i<='z';i++){
index[i-'a'][0]=s.indexOf(i);
index[i-'a'][1]=s.lastIndexOf(i)+1;
}
boolean changed=true;
while(changed) {
changed=false;
for(int i=0;i<26;i++){
for(int j=0;j<26;j++){
if(i==j) continue;
if(index[i][0]==-1) continue;
if(s.substring(index[i][0], index[i][1]).contains(String.valueOf((char)(j+'a')))) {
if(index[j][0]>=index[i][0] && index[j][1]<=index[i][1]) continue;
changed=true;
index[i][0]=Math.min(index[i][0], index[j][0]);
index[j][0]=Math.min(index[i][0], index[j][0]);
index[i][1]=Math.max(index[i][1], index[j][1]);
index[j][1]=Math.max(index[i][1], index[j][1]);
}
}
}
}
List<String> list=new ArrayList<>();
for(int i=0;i<26;i++){
if(index[i][0]==-1) continue;
String str=s.substring(index[i][0], index[i][1]);
if(!list.contains(str)) list.add(str);
}
boolean[] hasSubStr=new boolean[list.size()];
for(int i=0;i<list.size();i++){
for(int j=0;j<list.size();j++){
if(i==j) continue;
if(list.get(i).contains(list.get(j))) hasSubStr[i]=true;
}
}
List<String> result=new ArrayList<>();
for(int i=0;i<list.size();i++){
if(!hasSubStr[i]) result.add(list.get(i));
}
return result;
}
}
四、5467. 找到最接近目标值的函数值
通过的用户数177
尝试过的用户数603
用户总通过次数186
用户总提交次数1437
题目难度Hard
Winston 构造了一个如上所示的函数 func 。他有一个整数数组 arr 和一个整数 target ,他想找到让 |func(arr, l, r) - target| 最小的 l 和 r 。
请你返回 |func(arr, l, r) - target| 的最小值。
请注意, func 的输入参数 l 和 r 需要满足 0 <= l, r < arr.length 。
示例 1:
输入:arr = [9,12,3,7,15], target = 5
输出:2
解释:所有可能的 [l,r] 数对包括 [[0,0],[1,1],[2,2],[3,3],[4,4],[0,1],[1,2],[2,3],[3,4],[0,2],[1,3],[2,4],[0,3],[1,4],[0,4]], Winston 得到的相应结果为 [9,12,3,7,15,8,0,3,7,0,0,3,0,0,0] 。最接近 5 的值是 7 和 3,所以最小差值为 2 。
示例 2:
输入:arr = [1000000,1000000,1000000], target = 1
输出:999999
解释:Winston 输入函数的所有可能 [l,r] 数对得到的函数值都为 1000000 ,所以最小差值为 999999 。
示例 3:
输入:arr = [1,2,4,8,16], target = 0
输出:0
提示:
1 <= arr.length <= 10^51 <= arr[i] <= 10^60 <= target <= 10^7
题解
代码
class Solution {
public int closestToTarget(int[] arr, int target) {
int n=arr.length;
int[] dp=new int[n];
dp[0]=arr[0];
int min=Integer.MAX_VALUE;
for(int i=1;i<n;i++){
if(arr[i]==target) return 0;
if(arr[i]<target) dp[i]=arr[i];
if(arr[i]>target) {
if(arr[i-1]<target) dp[i]=arr[i];
else dp[i]=dp[i-1]&arr[i];
}
min=Math.min(min, Math.abs(target-dp[i]));
}
return min;
}
}