机器学习笔记（三十一）：集成学习

凌云时刻 · 技术

导读：到目前为止，我们已经学习了大概有八种机器学习的算法，其中有解决分类问题的，有解决回归问题的。这些算法其实没有谁是最好的，谁不好之说，反而应该将这些算法集合起来，发挥他们的最大价值。比如我们买东西或看电影之前，多少都会咨询身边的朋友，或去网上看看买家的评价，然后我们才会根据口碑好坏，或评价好坏决定买还是不买，看还是不看。在机器学习中，同样有这样的思路，这就是重要的集成学习。

作者 | 计缘

来源 | 凌云时刻（微信号：linuxpk）

集成学习

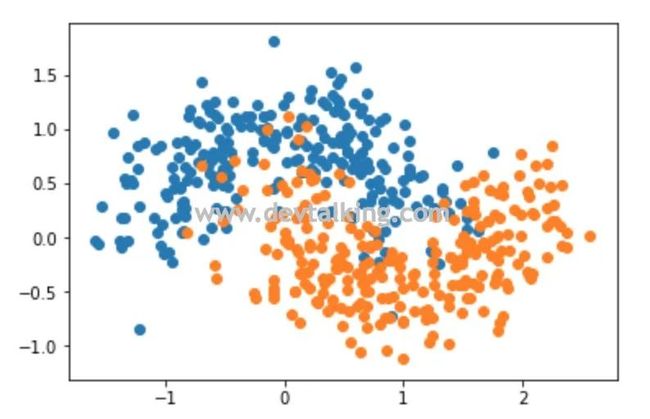
机器学习中的集成学习就是将选择若干算法，针对同一样本数据训练模型，然后看看结果，使用投票机制，少数服从多数，用多数算法给出的结果当作最终的决策依据，这就是集成学习的核心思路。下面我们先手动模拟一个使用集成学习解决回归问题的的示例：

 

import numpy as np import matplotlib.pyplot as plt from sklearn import datasets # 构建500个点的样本数据 X, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=666) # 绘制样本数据 plt.scatter(X[y==0, 0], X[y==0, 1]) plt.scatter(X[y==1, 0], X[y==1, 1]) plt.show()

分别使用逻辑回归、SVM、决策树针对上面的样本数据训练模型：

 

# 拆分样本数据 from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666) # 使用逻辑回归 from sklearn.linear_model import LogisticRegression log_clf = LogisticRegression() log_clf.fit(X_train, y_train) log_clf.score(X_test, y_test) # 结果 0.872 # 使用SVM from sklearn.svm import SVC svc_clf = SVC() svc_clf.fit(X_train, y_train) svc_clf.score(X_test, y_test) # 结果 0.89600000000000002 # 使用决策树 from sklearn.tree import DecisionTreeClassifier dt_clf = DecisionTreeClassifier() dt_clf.fit(X_train, y_train) dt_clf.score(X_test, y_test) # 结果 0.85599999999999998

 

可以看到，使用三种不同的分类算法训练出的模型，最后的   ‍‍评分都不尽相同。下面我们使用投票的方式，选择出最终预测值，具体思路是先求出三种模型对测试数据的预测结果，将三个结果向量相加，得到新的结果向量，因为分类只有0和1，所以新的结果向量里的值最大为3，最小为0。然后通过Fancy Index的方式，求出三种模型预测中至少有2种预测为1的，才真正认为是1的分类，那么也就是新结果向量里大于等于2的结果，其余小于2的都认为是0的分类：

  

# 求出三种模型对测试数据的预测结果 y_predict1 = log_clf.predict(X_test) y_predict2 = svc_clf.predict(X_test) y_predict3 = dt_clf.predict(X_test) y_predict = np.array((y_predict1 + y_predict2 + y_predict3) >= 2, dtype='int') # 计算最终的评分 from sklearn.metrics import accuracy_score accuracy_score(y_test, y_predict) # 结果 0.88800000000000001

上面的示例是我们手动使用三种算法的结果通过投票方式求得了最终的决策依据。其实Scikit Learn中已经为我们封装了这种方式，名为VotingClassifier，既投票分类器：

 

# 引入投票分类器 from sklearn.ensemble import VotingClassifier # VotingClassifier和Pipeline的用法非常类似，这里的voting="hard"可以先忽略 voting_clf = VotingClassifier(estimators=[ ("log_clf", LogisticRegression()), ("svm_clf", SVC()), ("dt_clf", DecisionTreeClassifier(random_state=666)) ], voting="hard") voting_clf.fit(X_train, y_train) voting_clf.score(X_test, y_test) # 结果 0.88800000000000001

可以看到，使用VotingClassifier最后的评分和我们手动模拟的是一致的。

Soft Voting

在上一节中，Scikit Learn提供的VotingClassifier有一个参数voting，我们传了hard这个值。其实这个参数就表示投票的方式，hard代表的就是少数服从多数的机制。

但是，其实在很多时候少数服从多数得到的结果并不是正确的，这个在日常生活中其实很常见，所谓真理掌握在少数人手里就是这个意思。所以更合理的投票机制应该是对投票人加以权重值，投票人越专业，越权威，那么权重值就应该高一些。就好比歌唱比赛，评委有三类人，第一类是音乐制作人，特点是人少，但权重值高，第二类是职业歌手，人数次之，权重值也次之，第三类是普通观众，这类人人数最多，但是权重值也最低。那么决定选手去留还是掌握在少数的音乐制作人和职业歌手这些评委。这个思路其实就是Soft Voting。

再举一个示例，假设有5个模型，针对同一个二分类问题，将每种类别都计算出了概率：

• 模型1 A-99%，B-1%

• 模型2 A-49%，B-51%

• 模型3 A-40%，B-60%

• 模型4 A-90%，B-10%

• 模型5 A-30%，B-70%

从上面的数据，明显可以得到，整体的分类应该B，因为模型2、模型3、模型5的结论都是B，所以按照Hard Voting方式，少数服从多数，那整体的类别会定为B。

但是我们可以换个角度去看问题，模型1和模型4对判定为类别A的概率都在90%以上，说明非常笃定。而模型2、模型3、模型5虽然结论为类别B，但是类别A和类别B的判定概率相差并不是很大。而我们将五种模型对类别A、类别B的概率加起来就可以明显的看到，判定为类别A的总概率为：

   

‍‍

而判定为类别B的总概率为：

   

显然判定为类别A的总概率要远高于类别B，那么整体类别应该是A。

以上模型判定类别的概率其实就可以理解为权重值。所以Soft Voting要求集合里的每一个模型都能估计出类别的概率。那么我们来看看我们已经了解过的机器学习算法哪些是支持概率的：

• 逻辑回归算法本身就是基于概率模型的，通过Sigmoid函数计算概率。

• kNN算法也是支持估计概率的，如果和预测点相邻的3个点，有2个点是红色，1个是蓝色，那么可以很容计算出红色类别的概率是   ，蓝色类别的概率是   。

• 决策树算法也是支持估计概率的，它的思路和kNN的很相近，每个叶子节点中如果信息熵或基尼系数不为0，那么就肯定至少包含2种以上的类别，那么用一个类别的数量除以所有类别的数据就能得到概率。

• SVM算法本身是不能够天然支持估计概率的。不过Scikit Learn中提供的SVC通过其他方式实现了估计概率的能力，代价就是增加了算法的时间复杂度和训练时间。它有一个probability参数，默认为false既不支持估计概率，如果显示传入true，那么就会启用估计概率的能力。

下面来看看Soft Voting如何使用：

 

# 还是使用上一节的数据，同样构建VotingClassifier，voiting参数传入soft。这里注意SVC要显示传入probability=True voting_clf1 = VotingClassifier(estimators=[ ("log_clf", LogisticRegression()), ("svm_clf", SVC(probability=True)), ("dt_clf", DecisionTreeClassifier(random_state=666)) ], voting="soft") voting_clf1.fit(X_train, y_train) voting_clf1.score(X_test, y_test) # 结果 0.89600000000000002

可以看到Soft Voting相比较Hard Voting，预测评分是有提高的。

Bagging

上两节主要介绍了集成学习的原理。那么就这个原理而言，它的好坏是有一个基本的先决条件的。对于投票机制而言，5个人投票和1000个人投票得到的结果，毫无疑问是后者更具有说服力。所以前两节我们只使用了三个机器学习算法训练的模型去投票是不具有很强的说服力的。那么问题来了，我们如何能有更多的模型，来作为投票者呢？这就是这一节要说的取样问题。

我们知道机器学习算法是有限的，有几十个就顶破天了，所以用不同的算法这条路是行不通的，那么我们就从同一种算法的不同模型这个思路入手。基本思路就是使用一种机器学习算法，创建更多的子模型，然后集成这些子模型的意见进行投票，有个前提是子模型之间不能一致，要有差异性。这一点大家应该很好理解，模型之间的差异性越大，投票才有意义。

那么如何创建子模型的差异性呢？通常的做法是训练每个子模型时只看样本数据的一部分，比如一共有1000个样本数据，每个子模型只看100个样本数据，因为样本数据有差异性，所以训练出的子模型之间就自然存在差异性了。这时问题又来了，训练子模型时只这么少的样本数据，那么每个子模型的准确率自然会比较低。此时就应征了，人多力量大，一把筷子折不断的道理。

假设有三个子模型，每个子模型的准确率只有51%，为什么要用51%作为示例呢，因为投硬币的概率都有50%，所以比它只高一点，算是很低的准确率了。那么整体的准确率为：

   

三个准确率为51%的子模型，可以使整体的准确率提高至51.5%。那如果是500个子模型，整体的准确率会提升至：

   

可见当子模型的数量增加时，同时会增加整体的准确率。所以其实子模型并不需要太高的准确率。

END

往期精彩文章回顾

机器学习笔记（三十）：基尼系数、CART

机器学习笔记（二十九）：决策树、信息熵

机器学习笔记（二十八）：高斯核函数

机器学习笔记（二十七）：核函数（Kernel Function）

机器学习笔记（二十六）：支撑向量机（SVM）(2)

机器学习笔记（二十五）：支撑向量机（SVM）

机器学习笔记（二十四）：召回率、混淆矩阵

机器学习笔记（二十三）：算法精准率、召回率

机器学习笔记（二十二）：逻辑回归中使用模型正则化

机器学习笔记（二十一）：决策边界

长按扫描二维码关注凌云时刻

每日收获前沿技术与科技洞见